Задания на нахождение площади сектора круга из открытого банка ФИПИ, которые могут попасться вам на реальном ОГЭ по математике в этом году.
Реальные задания по геометрии из банка ФИПИ
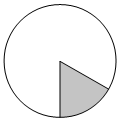
Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Решение 2-мя способами:
Круг составляет 360°, его площадь равна 90.
Пусть х - площадь сектора, центральный угол которого равен 60°. Составим пропорцию.
угол площадь
360° - 90
60° - х
360/60 = 90/x
х = (90 * 60) / 360 = 5400 / 360 = 15
Значит, площадь сектора равна 15 кв. единиц.
Ответ: 15
2 способ
Круг составляет 360°, значит центральный угол
360 : 60 = 6 - это шестая часть круга
Тогда площадь сектора будет шестой частью площади круга:
90 : 6 = 15 кв. единиц
Ответ: 15
8274E3
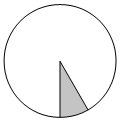
Площадь круга равна 120. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Решение:
Круг составляет 360°, его площадь равна 120.
Пусть х - площадь сектора, центральный угол которого равен 30°. Составим пропорцию.
угол площадь
360° - 120
30° - х
360/30 = 120/x
х = (120 * 30) / 360 = 3600 / 360 = 10
Значит, площадь сектора равна 10 кв. единиц.
Ответ: 10
F8ABE2

Площадь круга равна 112. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Решение:
Круг составляет 360°, его площадь равна 112.
Пусть х - площадь сектора, центральный угол которого равен 45°. Составим пропорцию.
угол площадь
360° - 112
45° - х
360/45 = 112/x
х = (112 * 45) / 360 = 5040 / 360 = 14
Значит, площадь сектора равна 14 кв. единиц.
Ответ: 14
6071D2
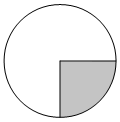
Площадь круга равна 72. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
Решение:
Круг составляет 360°, его площадь равна 72.
Пусть х - площадь сектора, центральный угол которого равен 90°. Составим пропорцию.
угол площадь
360° - 72
90° - х
360/90 = 72/x
х = (90 * 72) / 360 = 6480/ 360 = 18
Значит, площадь сектора равна 18 кв. единиц.
Ответ: 18
EB3A54
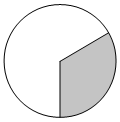
Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°.
Решение:
Круг составляет 360°, его площадь равна 69.
Пусть х - площадь сектора, центральный угол которого равен 120°. Составим пропорцию.
угол площадь
360° - 69
120° - х
360/120 = 69/x
х = (120 * 69) / 360 = 8280 / 360 = 23
Значит, площадь сектора равна 23 кв. единицы.
Ответ: 23
D101DC

Площадь круга равна 123. Найдите площадь сектора этого круга, центральный угол которого равен 120°.
Решение:
Круг составляет 360°, его площадь равна 123.
Пусть х - площадь сектора, центральный угол которого равен 120°. Составим пропорцию.
угол площадь
360° - 123
120° - х
360/120 = 123/x
х = (123 * 120) / 360 = 14760 / 360 = 41
Значит, площадь сектора равна 41 кв. единица.
Ответ: 41
42ACF8

Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
Решение:
Круг составляет 360°, его площадь равна 88.
Пусть х - площадь сектора, центральный угол которого равен 90°. Составим пропорцию.
угол площадь
360° - 88
90° - х
360/90 = 88/x
х = (90 * 88) / 360 = 7920 / 360 = 22
Значит, площадь сектора равна 22 кв. единиц.
Ответ: 22
52A0D2

Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Решение:
Круг составляет 360°, его площадь равна 78.
Пусть х - площадь сектора, центральный угол которого равен 60°. Составим пропорцию.
угол площадь
360° - 78
60° - х
360/60 = 78/x
х = (60 * 78) / 360 = 4680 / 360 = 13
Значит, площадь сектора равна 13 кв. единиц.
Ответ: 13
68A55F

Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Решение:
Круг составляет 360°, его площадь равна 180.
Пусть х - площадь сектора, центральный угол которого равен 30°. Составим пропорцию.
угол площадь
360° - 180
30° - х
360/30 = 180/x
х = (30 * 180) / 360 = 5400 / 360 = 15
Значит, площадь сектора равна 15 кв. единиц.
Ответ: 15
0E345D

Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Решение:
Круг составляет 360°, его площадь равна 88.
Пусть х - площадь сектора, центральный угол которого равен 45°. Составим пропорцию.
угол площадь
360° - 88
45° - х
360/45 = 88/x
х = (45 * 88) / 360 = 3960 / 360 = 11
Значит, площадь сектора равна 11 кв. единиц.
Ответ: 11
7CA3AC

