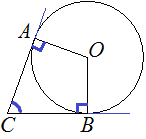В открытом банке заданий ФИПИ очень много задач по геометрии с кратким ответом, в которых нужно найти тот или иной угол в треугольнике, четырехугольнике, трапеции и др. Известные данные тоже разнятся, формулы используются в зависимости от того, что нам дано.
Вспоминаем, что сумма углов любого треугольника равна 180о, что сумма смежных углов равна так же 180о, и сумма противоположных углов вписанного четырехугольника тоже равна 180о. Вспоминаем так же тему градусная мера дуги, что вписанный угол равен половине дуги, на которую опирается, а центральный - дуге, на которую опирается; что вся дуга окружности 360°, а диаметр делит ее пополам; что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой.
Многие из этих заданий решаются не то что просто, а элементарно, в уме. В бланк вам нужно будет записать лишь число. Вот все эти задания.
Реальные задания по геометрии из банка ФИПИ
Найти угол в прямоугольном треугольнике по двум известным
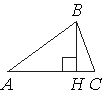
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 37°
∠AHB = 90°
∠ABH = 180 - 90 - 37 = 53°
Ответ: 53
3A1100
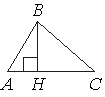
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=46°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 46°
∠AHB = 90°
∠ABH = 180 - 90 - 46 = 44°
Ответ: 44
4D64A2
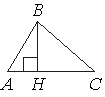
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=55°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 55°
∠AHB = 90°
∠ABH = 180 - 90 - 55 = 35°
Ответ: 35
6D0B15
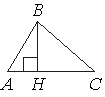
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=64°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 64°
∠AHB = 90°
∠ABH = 180 - 90 - 64 = 26°
Ответ: 26
EF47C9
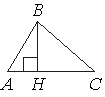
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=73°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 73°
∠AHB = 90°
∠ABH = 180 - 90 - 73 = 17°
Ответ: 17
238B6C
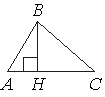
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=82°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 82°
∠AHB = 90°
∠ABH = 180 - 90 - 82 = 8°
Ответ: 8
AA90F7
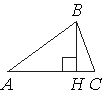
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=28°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 28°
∠AHB = 90°
∠ABH = 180 - 90 - 28 = 62°
Ответ: 62
2D8A31
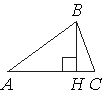
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=19°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 19°
∠AHB = 90°
∠ABH = 180 - 90 - 19 = 71°
Ответ: 71
CD3F90
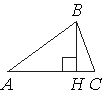
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=9°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 9°
∠AHB = 90°
∠ABH = 180 - 90 - 9 = 81°
Ответ: 81
2871C3
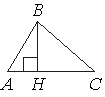
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=48°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 48°
∠AHB = 90°
∠ABH = 180 - 90 - 48 = 42°
Ответ: 42
5C293A
Найти смежный угол
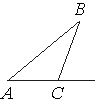
В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-133°=47°
Ответ: 47
45DD3F

В треугольнике ABC угол C равен 142°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-142°=38°
Ответ: 38
1BA068

В треугольнике ABC угол C равен 151°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-151°=29°
Ответ: 29
4007B1

В треугольнике ABC угол C равен 159°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-159°=21°
Ответ: 21
EAE145

В треугольнике ABC угол C равен 168°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-168°=12°
Ответ: 12
E43EDE

В треугольнике ABC угол C равен 177°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-177°=3°
Ответ: 3
80A959

В треугольнике ABC угол C равен 124°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-124°=56°
Ответ: 56
4C1E2E

В треугольнике ABC угол C равен 115°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-115°=65°
Ответ: 65
AB056D

В треугольнике ABC угол C равен 106°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-106°=74°
Ответ: 74
53EC35

В треугольнике ABC угол C равен 97°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-97°=83°
Ответ: 83
0B25FB
Найти угол в треугольнике по двум известным углам
В треугольнике два угла равны 57° и 86°. Найдите его третий угол. Ответ дайте в градусах.
Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (57° + 86°) = 37°
Ответ: 37
632955
В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (72° + 42°) = 66°
Ответ: 66
B44B61
В треугольнике два угла равны 27° и 79°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (27° + 79°) = 74°
Ответ: 74
5FF3E9
В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (36° + 73°) = 71°
Ответ: 71
A4417F
В треугольнике два угла равны 31° и 94°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (31° + 94°) = 55°
Ответ: 55
A35B10
В треугольнике два угла равны 47° и 64°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (47° + 64°) = 69°
Ответ: 69
FCCC67
В треугольнике два угла равны 54° и 58°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (54° + 58°) = 68°
Ответ: 68
32B7F7
В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (46° + 78°) = 56°
Ответ: 56
DBFC5D
В треугольнике два угла равны 38° и 89°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (38° + 89°) = 53°
Ответ: 53
4BF51E
В треугольнике два угла равны 28° и 93°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (28° + 93°) = 59°
Ответ: 59
F145C7
В треугольнике два угла равны 48° и 65°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (48° + 65°) = 67°
Ответ: 67
67DB39
В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (43° + 88°) = 49°
Ответ: 49
FDEABD
Один из острых углов прямоугольного треугольника равен 34°. Найдите его другой острый угол. Ответ дайте в градусах.
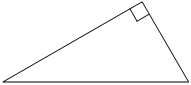
Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 34° = 56°
Ответ: 56
FA57C4
Один из острых углов прямоугольного треугольника равен 26°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 26° = 64°
Ответ: 64
E36D97
Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 43° = 47°
Ответ: 47
0CD2B6
Один из острых углов прямоугольного треугольника равен 18°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 18° = 72°
Ответ: 72
898058
Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 23° = 67°
Ответ: 67
D4F4F0
Один из острых углов прямоугольного треугольника равен 48°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 48° = 42°
Ответ: 42
0EB756
Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 21° = 69°
Ответ: 69
455DB7
Один из острых углов прямоугольного треугольника равен 36°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 36° = 54°
Ответ: 54
98EE2C
Один из острых углов прямоугольного треугольника равен 53°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 53° = 37°
Ответ: 37
421524
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 57° = 33°
Ответ: 33
11BB1D
Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 63° = 27°
Ответ: 27
987BBE
Один из острых углов прямоугольного треугольника равен 68°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 68° = 22°
Ответ: 22
595130
Найти угол у основания в равнобедренном треугольнике
В треугольнике ABC известно, что AB=BC, ∠ABC=108°. Найдите угол BCA. Ответ дайте в градусах.
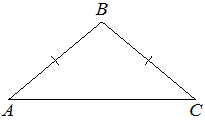
Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 108°) / 2 = 36°
Ответ: 36
64AC4E
В треугольнике ABC известно, что AB=BC, ∠ABC=106°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 106°) / 2 = 37°
Ответ: 37
4FF4DF
В треугольнике ABC известно, что AB=BC, ∠ABC=104°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 104°) / 2 = 38°
Ответ: 38
CD563C
В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 102°) / 2 = 39°
Ответ: 39
3CF02F
В треугольнике ABC известно, что AB=BC, ∠ABC=128°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 128°) / 2 = 26°
Ответ: 26
F172BF
В треугольнике ABC известно, что AB=BC, ∠ABC=126°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 126°) / 2 = 27°
Ответ: 27
879265
В треугольнике ABC известно, что AB=BC, ∠ABC=124°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 124°) / 2 = 28°
Ответ: 28
DB94FB
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 122°) / 2 = 29°
Ответ: 29
524060
В треугольнике ABC известно, что AB=BC, ∠ABC=148°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 148°) / 2 = 16°
Ответ: 16
C33E1D
В треугольнике ABC известно, что AB=BC, ∠ABC=146°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 146°) / 2 = 17°
Ответ: 17
A51073
В треугольнике ABC известно, что AB=BC, ∠ABC=144°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 144°) / 2 = 18°
Ответ: 18
6A6370
В треугольнике ABC известно, что AB=BC, ∠ABC=142°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 142°) / 2 = 19°
Ответ: 19
0A21C6
Найти угол, полученный при делении биссектрисой
В треугольнике ABC известно, что ∠BAC=82°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
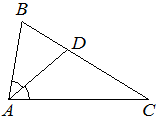
Решение:
Биссектриса делит угол пополам, значит
∠BAD = 82 / 2 = 41°
Ответ: 41
96298E
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 62 / 2 = 31°
Ответ: 31
959276
В треугольнике ABC известно, что ∠BAC=42°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
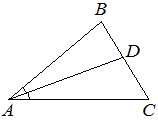
Решение:
Биссектриса делит угол пополам, значит
∠BAD = 42 / 2 = 21°
Ответ: 21
F7649E
В треугольнике ABC известно, что ∠BAC=84°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 84 / 2 = 42°
Ответ: 42
98F32B
В треугольнике ABC известно, что ∠BAC=86°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 86 / 2 = 43°
Ответ: 43
17189A
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 64 / 2 = 32°
Ответ: 32
85BF87
В треугольнике ABC известно, что ∠BAC=68°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 68 / 2 = 34°
Ответ: 34
66F995
В треугольнике ABC известно, что ∠BAC=46°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 46 / 2 = 23°
Ответ: 23
5F05FB
В треугольнике ABC известно, что ∠BAC=48°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 48 / 2 = 24°
Ответ: 24
39A249
В треугольнике ABC известно, что ∠BAC=24°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 24 / 2 = 12°
Ответ: 12
249757
В треугольнике ABC известно, что ∠BAC=26°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 26 / 2 = 13°
Ответ: 13
15F118
В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол пополам, значит
∠BAD = 28 / 2 = 14°
Ответ: 14
C5592F
Найти угол четырехугольника, вписанного в окружность
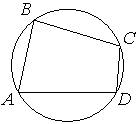
Угол A четырёхугольника ABCD, вписанного в окружность, равен 82°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 82° = 98°
Ответ: 98
E0EAD5

Угол A четырёхугольника ABCD, вписанного в окружность, равен 48°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 48° = 132°
Ответ: 132
39B2FC

Угол A четырёхугольника ABCD, вписанного в окружность, равен 71°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 71° = 109°
Ответ: 109
5821D7

Угол A четырёхугольника ABCD, вписанного в окружность, равен 56°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 56° = 124°
Ответ: 124
BBAB97
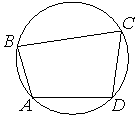
Угол A четырёхугольника ABCD, вписанного в окружность, равен 112°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 112° = 68°
Ответ: 68
7EE52B

Угол A четырёхугольника ABCD, вписанного в окружность, равен 78°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 78° = 102°
Ответ: 102
C2DCFD
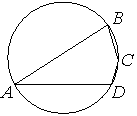
Угол A четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 37° = 143°
Ответ: 143
752E75

Угол A четырёхугольника ABCD, вписанного в окружность, равен 62°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 62° = 118°
Ответ: 118
2FF9D2
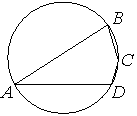
Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 33° = 147°
Ответ: 147
DD88DC

Угол A четырёхугольника ABCD, вписанного в окружность, равен 54°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 54° = 126°
Ответ: 126
7A7116
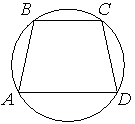
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 81°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 81° = 99°
Ответ: 99
0AEB63

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 47°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 47° = 133°
Ответ: 133
A54182

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 69°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 69° = 111°
Ответ: 111
6E696F

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 55°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 55° = 125°
Ответ: 125
ED02DC
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 111°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 111° = 69°
Ответ: 69
5D89E6

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 77°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 77° = 103°
Ответ: 103
0B2EF1

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 36°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 36° = 144°
Ответ: 144
5435EA

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 61°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 61° = 119°
Ответ: 119
C2A29C

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 32° = 148°
Ответ: 148
34CB26

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 53°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 53° = 127°
Ответ: 127
C0C769

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 79°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 79° = 101°
Ответ: 101
5F0DA8

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 46°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 46° = 134°
Ответ:
3CB110

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 68°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 68° = 112°
Ответ: 112
BA0CAE

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 54°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 54° = 126°
Ответ: 126
953423
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 108°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 108° = 72°
Ответ: 72
443158

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 76°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 76° = 104°
Ответ: 104
9CDD2B

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 35°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 35° = 145°
Ответ: 145
54330A

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 59°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 59° = 121°
Ответ: 121
D5834D

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 31° = 149°
Ответ: 149
0C87C3

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 52° = 128°
Ответ: 128
89A311
Найти угол между хордой и касательной к окружности
На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=92°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-92) : 2 = 88 : 2 = 44°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 44°
∠ABC = 46°
Ответ: 46
F5B110
На окружности отмечены точки A и B так, что меньшая дуга AB равна 134°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=134°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-134) : 2 = 46 : 2 = 23°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 23°
∠ABC = 67°
Ответ: 67
457246
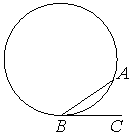
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=66°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-66) : 2 = 114 : 2 = 57°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 57°
∠ABC = 33°
Ответ: 33
296C71
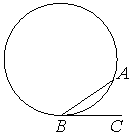
На окружности отмечены точки A и B так, что меньшая дуга AB равна 50°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=50°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-50) : 2 = 130 : 2 = 65°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 65°
∠ABC = 25°
Ответ: 25
F8F49D
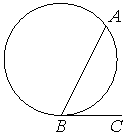
На окружности отмечены точки A и B так, что меньшая дуга AB равна 106°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=106°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-106) : 2 = 74 : 2 = 37°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 37°
∠ABC = 53°
Ответ: 53
E48B3F
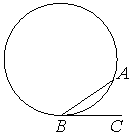
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=72°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-72) : 2 = 108 : 2 = 54°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 54°
∠ABC = 36°
Ответ: 36
7490EE
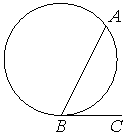
На окружности отмечены точки A и B так, что меньшая дуга AB равна 168°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=168°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-168) : 2 = 12 : 2 = 6°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 6°
∠ABC = 84°
Ответ: 84
F9170A
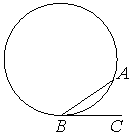
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=56°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-56) : 2 = 124 : 2 = 62°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 62°
∠ABC = 28°
Ответ: 28
132C9B
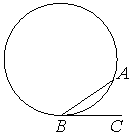
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=26°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-26) : 2 = 154 : 2 = 77°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 77°
∠ABC = 13°
Ответ: 13
74F521
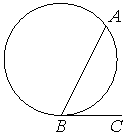
На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение:
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=152°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-152) : 2 = 28 : 2 = 14°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 14°
∠ABC = 76°
Ответ: 76
CFAAB6
Найти угол вписанного в окружность четырехугольника
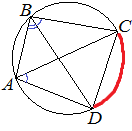
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 39°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте в градусах.
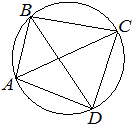
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 55°
∠ABC = ∠ABD + ∠CBD = 39° + 55° = 94°
Ответ: 94
CBE537
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 80°, угол CAD равен 34°. Найдите угол ABC. Ответ дайте в градусах.
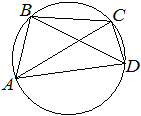
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 34°
∠ABC = ∠ABD + ∠CBD = 80° + 34° = 114°
Ответ: 114
BA2500
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 82°, угол CAD равен 28°. Найдите угол ABC. Ответ дайте в градусах.
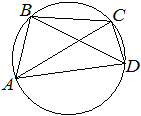
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 28°
∠ABC = ∠ABD + ∠CBD = 82° + 28° = 110°
Ответ: 110
FF8B8C
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 51°, угол CAD равен 42°. Найдите угол ABC. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 42°
∠ABC = ∠ABD + ∠CBD = 51° + 42° = 93°
Ответ: 93
314B4D
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 16°, угол CAD равен 32°. Найдите угол ABC. Ответ дайте в градусах.
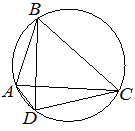
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 32°
∠ABC = ∠ABD + ∠CBD = 16° + 32° = 48°
Ответ: 48
4D798A
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 78°, угол CAD равен 40°. Найдите угол ABC. Ответ дайте в градусах.
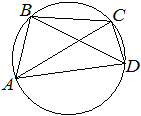
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 40°
∠ABC = ∠ABD + ∠CBD = 78° + 40° = 118°
Ответ: 118
88F766
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 85°, угол CAD равен 19°. Найдите угол ABC. Ответ дайте в градусах.
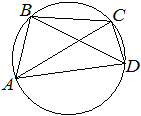
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 19°
∠ABC = ∠ABD + ∠CBD = 85° + 19° = 104°
Ответ: 104
2E1DDF
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 38°, угол CAD равен 54°. Найдите угол ABC. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 54°
∠ABC = ∠ABD + ∠CBD = 38° + 54° = 92°
Ответ: 92
80EA92
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 77°, угол CAD равен 43°. Найдите угол ABC. Ответ дайте в градусах.
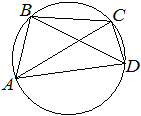
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 43°
∠ABC = ∠ABD + ∠CBD = 77° + 43° = 120°
Ответ: 120
3B61EF
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 25°, угол CAD равен 41°. Найдите угол ABC. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 41°
∠ABC = ∠ABD + ∠CBD = 25° + 41° = 66°
Ответ: 66
812E73
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 49°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 70° - 49° = 21°
Ответ: 21
7BE617
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах.
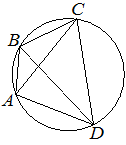
Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 81°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 134° - 81° = 53°
Ответ: 53
12F228
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 38°, угол CAD равен 33°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 33°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 38° - 33° = 5°
Ответ: 5
CBBF04
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 83°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 138° - 83° = 55°
Ответ: 55
A625E2
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 120°, угол CAD равен 74°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 74°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 120° - 74° = 46°
Ответ: 46
E74D85
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 112°, угол CAD равен 70°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 70°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 112° - 70° = 42°
Ответ: 42
1B393E
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 56°, угол CAD равен 42°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 42°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 56° - 42° = 14°
Ответ: 14
3739E9
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 54°, угол CAD равен 41°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 41°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 54° - 41° = 13°
Ответ: 13
A8980C
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 132°, угол CAD равен 80°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 80°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 132° - 80° = 52°
Ответ: 52
939A13
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 60°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 92° - 60° = 32°
Ответ: 32
BE804A
Найти угол внутри вписанной в угол окружности
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
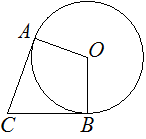
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 83° = 97°
Ответ: 97
1BCD9A
В угол C величиной 40° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 40° = 140°
Ответ: 140
7B2CEA
В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
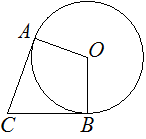
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 79° = 101°
Ответ: 101
FC1B6C
В угол C величиной 107° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
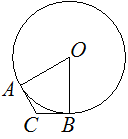
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 107° = 73°
Ответ: 73
9B6BD0
В угол C величиной 84° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
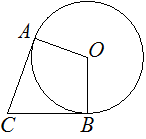
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 84° = 96°
Ответ: 96
4F5AEF
В угол C величиной 72° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
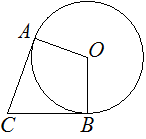
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 72° = 108°
Ответ: 108
AD7805
В угол C величиной 157° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
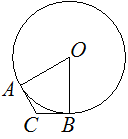
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 157° = 23°
Ответ: 23
FD5FFD
В угол C величиной 115° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
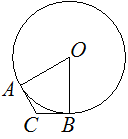
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 115° = 65°
Ответ: 65
B1E33A
В угол C величиной 133° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
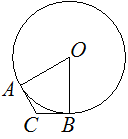
Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 133° = 47°
Ответ: 47
43E6E2
В угол C величиной 18° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90° каждый.
Сумма углов четырёхугольника равна 360°, отсюда:
∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 18° = 162°
Ответ: 162
C05BD0
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.
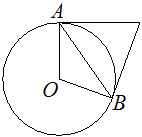
Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 72°) / 2 = 54°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 54° = 36°
Ответ: 36
2 способ
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 72°) / 2 = 54°
Угол между касательной и хордой равен половине дуги, которую он заключает, значит,
дуга AB = 54 * 2 = 108°.
Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 108°.
Рассмотрим треугольник AOB, он равнобедренный, следовательно,
∠OAB = ∠ ABO = (180° - 108°) / 2 = 36°.
Ответ: 36.
EC1F63
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 52°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 52°) / 2 = 64°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 64° = 26°
Ответ: 26
804D28
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 86°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 86°) / 2 = 47°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 47° = 43°
Ответ: 43
5D4484
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 38°. Найдите угол ABO. Ответ дайте в градусах.
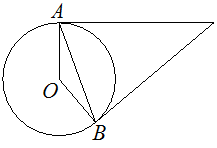
Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 38°) / 2 = 71°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 71° = 19°
Ответ: 19
7D4D9B
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 56°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 56°) / 2 = 62°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 62° = 28°
Ответ: 28
6E857B
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 68°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 68°) / 2 = 56°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 56° = 34°
Ответ: 34
CB2361
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 82°) / 2 = 49°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 49° = 41°
Ответ: 41
59C247
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 42°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 42°) / 2 = 69°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 69° = 21°
Ответ: 21
E068C3
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 36°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 36°) / 2 = 72°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 72° = 18°
Ответ: 18
C70E95
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 88°. Найдите угол ABO. Ответ дайте в градусах.

Решение:
С
Обозначим точку пересечения касательных как С.
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 88°) / 2 = 46°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 46° = 44°
Ответ: 44
199FBC
Найти угол во вписанном в окружность треугольнике
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
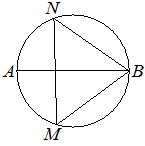
Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 36° = 72°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 72° = 108°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
108°/2 = 54°.
Ответ: 54.
2360D1
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
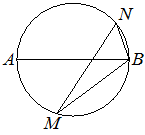
Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 69° =138°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 138° = 42°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
42°/2 = 21°.
Ответ: 21.
FE43C5
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=43°. Найдите угол NMB. Ответ дайте в градусах.
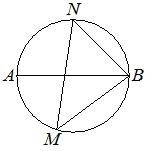
Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 43° = 86°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 86° = 94°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
94°/2 = 47°.
Ответ: 47.
E17B64
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=48°. Найдите угол NMB. Ответ дайте в градусах.

Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 48° = 96°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 96° = 84°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
84°/2 = 42°.
Ответ: 42.
847AFF
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=32°. Найдите угол NMB. Ответ дайте в градусах.

Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 32° = 64°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 64° = 116°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
116°/2 = 58°.
Ответ: 58.
44DCE7
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=34°. Найдите угол NMB. Ответ дайте в градусах.

Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 34° = 68°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 68° = 112°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
112°/2 = 56°.
Ответ: 56.
F368CE
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.

Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 41° = 82°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 82° = 98°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
98°/2 = 49°.
Ответ: 49.
4CDB9E
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=71°. Найдите угол NMB. Ответ дайте в градусах.

Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 71° = 142°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 142° = 38°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
38°/2 = 19°.
Ответ: 19.
A17BC2
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=68°. Найдите угол NMB. Ответ дайте в градусах.

Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 68° = 136°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 136° = 44°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
44°/2 = 22°.
Ответ: 22.
5DB6C1
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=44°. Найдите угол NMB. Ответ дайте в градусах.

Решение:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 44° = 88°.
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 88° = 92°.
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
92°/2 = 46°.
Ответ: 46.
C5328F
Найти угол между точками на окружности и центром
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=75° и ∠OAB=43°. Найдите угол BCO. Ответ дайте в градусах.
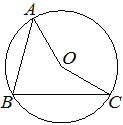
Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника ∠OAB = ∠ABO = 43°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 75° − 43° = 32°.
Ответ: 32
A6485A
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=56° и ∠OAB=15°. Найдите угол BCO. Ответ дайте в градусах.
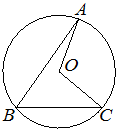
Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника ∠OAB = ∠ABO = 15°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 56° − 15° = 41°.
Ответ: 41
E586F4
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=44° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.

Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 13°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 44° − 13° = 31°.
Ответ: 31
3D67DD
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=54° и ∠OAB=41°. Найдите угол BCO. Ответ дайте в градусах.
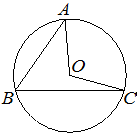
Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 41°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 54° − 41° = 13°.
Ответ: 13
398DD1
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=62° и ∠OAB=53°. Найдите угол BCO. Ответ дайте в градусах.

Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 53°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 62° − 53° = 9°.
Ответ: 9
24A76B
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=46° и ∠OAB=28°. Найдите угол BCO. Ответ дайте в градусах.

Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 28°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 46° − 28° = 18°.
Ответ: 18
E23357
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=69° и ∠OAB=48°. Найдите угол BCO. Ответ дайте в градусах.

Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 48°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 69° − 48° = 21°.
Ответ: 21
578067
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=22°. Найдите угол BCO. Ответ дайте в градусах.
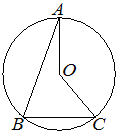
Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 22°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 71° − 22° = 49°.
Ответ: 49
69D701
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=61° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.

Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 8°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 61° − 8° = 53°.
Ответ: 53
5BDF8D
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=76° и ∠OAB=33°. Найдите угол BCO. Ответ дайте в градусах.

Решение:
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 33°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 76° − 33° = 43°.
Ответ: 43
69CED2
Найти угол во вписанном в окружность треугольнике
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите угол BOC. Ответ дайте в градусах.
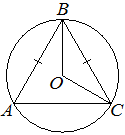
Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 57° = 123 °.
Ответ: 123
7BF1F3
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите угол BOC. Ответ дайте в градусах.
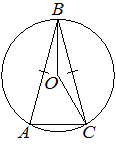
Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 25° = 155 °.
Ответ: 155
D62FBA
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=123°. Найдите угол BOC. Ответ дайте в градусах.
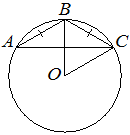
Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 123° = 57°.
Ответ: 57
7F601C
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите угол BOC. Ответ дайте в градусах.
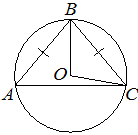
Решение 2-мя способами:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2 = (180° - 79°) / 2 = 50,5° .
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 50,5° * 2 = 101°.
Ответ: 101
2 способ
∠ABC = 79 ° - вписанный, поэтому он равен половине дуги, на которую опирается ⇒ дуга АС = 2 * 79° = 158°
∠BOC - центральный, поэтому он равен величине дуги, на которую опирается.
Дуга ВС = дуге АВ, поскольку вписанный треугольник равнобедренный.
∠BOC = 1/2 дуги АВС = 1/2 (360° - дуга АС) = 1/2 (360° - 158 °) = 202 /2 = 101
Ответ: 101
309189
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=32°. Найдите угол BOC. Ответ дайте в градусах.
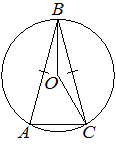
Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 32 = 148°.
Ответ: 148
3A7F9E
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=66°. Найдите угол BOC. Ответ дайте в градусах.
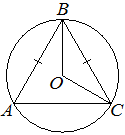
Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 66° = 114°.
Ответ: 114
8368D8
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=107°. Найдите угол BOC. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 107° = 73°.
Ответ: 73
19300A
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=88°. Найдите угол BOC. Ответ дайте в градусах.
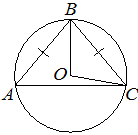
Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 88° = 92°.
Ответ: 92
A69CA2
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=119°. Найдите угол BOC. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 119° = 61°.
Ответ: 61
C26811
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=28°. Найдите угол BOC. Ответ дайте в градусах.
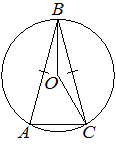
Решение:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 28° = 152°.
Ответ: 152
760A74
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 27°. Ответ дайте в градусах.
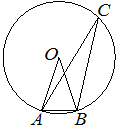
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 27° / 2 = 13,5°.
Ответ: 13,5
24D584
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 113°. Ответ дайте в градусах.
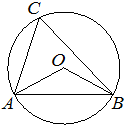
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 113° / 2 = 56,5°.
Ответ: 56,5
074CAF
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 67°. Ответ дайте в градусах.
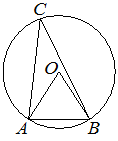
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 67° / 2 = 33,5°.
Ответ: 33,5
0B92BF
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 47°. Ответ дайте в градусах.
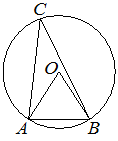
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 47° / 2 = 23,5°.
Ответ: 23,5
DE7F8E
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 167°. Ответ дайте в градусах.
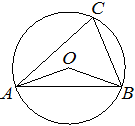
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 167° / 2 = 83,5°.
Ответ: 83,5
D00D8E
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 59°. Ответ дайте в градусах.
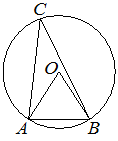
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 59° / 2 = 29,5°.
Ответ: 29,5
3A4AAE
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 73°. Ответ дайте в градусах.
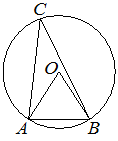
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 73° / 2 = 36,5°.
Ответ: 36,5
7533C8
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 115°. Ответ дайте в градусах.

Решение:
Угол AOB является центральным углом, ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 115° / 2 = 57,5°.
Ответ: 57,5
20B8B4
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 173°. Ответ дайте в градусах.

Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 173° / 2 = 86,5°.
Ответ: 86,5
9DA99C
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 153°. Ответ дайте в градусах.

Решение:
Угол AOB является центральным углом, ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 153° / 2 = 76,5°.
Ответ: 76,5
473A79
Найти угол между диаметром и хордой окружности
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.
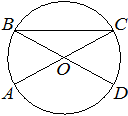
Решение 2-мя способами:
Смежные углы BOA и AOD образуют развёрнутый угол, поэтому их сумма равна 180°, откуда
∠AOB = 180° − 124° = 56°.
Угол AOB — центральный, следовательно, он равен дуге, на которую опирается,
угол ACB — вписанный, следовательно, он равен половине дуги, на которую опирается.
Поскольку углы AOB и ACB опираются на одну и ту же дугу, угол ACB равен половине угла AOB, то есть
∠ACB = 1/2 ∠AOB = 56 / 2 = 28°.
Ответ: 28
2 способ
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 124°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 124°) / 2 = 56° / 2 = 28°
Ответ: 28
80FB25
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 148°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 148°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 148°) / 2 = 32° / 2 = 16°
Ответ: 16
53AD0E
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 88°. Найдите угол ACB. Ответ дайте в градусах.
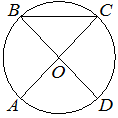
Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 88°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 88°) / 2 = 92° / 2 = 46°
Ответ: 46
10A0E2
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 114°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 114°) / 2 = 66° / 2 = 33°
Ответ: 33
5ED7FC
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 92°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 92°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 92°) / 2 = 88° / 2 = 44°
Ответ: 44
D96BAF
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 108°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 108°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 108°) / 2 = 72° / 2 = 36°
Ответ: 36
BC3721
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
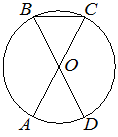
Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 50°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 50°) / 2 = 130° / 2 = 65°
Ответ: 65
91D482
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 74°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 74°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 74°) / 2 = 106° / 2 = 53°
Ответ: 53
D91FD7
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 44°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 44°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 44°) / 2 = 136° / 2 = 68°
Ответ: 68
34D194
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 86°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 86°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 86°) / 2 = 94° / 2 = 47°
Ответ: 47
24D2BC
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.

Решение 2-мя способами:
Угол ACB — вписанный, опирается на дугу AB, поэтому он равен половине дуги AB, значит величина дуги AB равна
2 · 79° = 158°.
Поскольку BD — диаметр, градусная мера дуги BAD равна 180°.
Градусная мера дуги AD равна разности градусных мер дуг BAD и AB:
дуга AD = 180° − 158° = 22°.
Угол AOD — центральный, поэтому он равен дуге, на которую опирается, следовательно, он равен 22°.
Ответ: 22
2 способ
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 79°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*79° = 22°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 22°
Ответ: 22
2438AC
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 54°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*54° = 72°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 72°
Ответ: 72
AEDABA
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 16°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 16°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*16° = 148°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 148°
Ответ: 148
3519DC
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 74°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*74° = 32°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 32°
Ответ: 32
5E6CD2
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 78°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 78°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*78° = 24°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 24°
Ответ: 24
1DC714
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 23°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 23°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*23° = 134°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 134°
Ответ: 134
58667F
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 59°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 59°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*59° = 62°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 62°
Ответ: 62
7CD3A9
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 19°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 19°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*19° = 142°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 142°
Ответ: 142
74C519
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 53°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 53°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*53° = 74°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 74°
Ответ: 74
66A5A3
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 62°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 62°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*62° = 56°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 56°
Ответ: 56
2933EB
Найти угол в треугольнике, вписанном в окружность
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 75°. Ответ дайте в градусах.
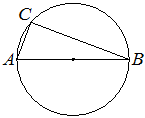
Решение 2-мя способами:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 75°= 15°
Ответ: 15
2 способ на случай, если забыли то, что написано выше
∠BAC = 75°, он вписанный, значит равен половине дуги, на которую опирается, отсюда
дуга ВС = 2∠BAC = 2 * 75 = 150°
Дуга АСВ отсекается диаметром, значит она равна 180°
дуга АС = дуга АСВ - дуга ВС = 180° - 150° = 30°
∠ABC вписанный, опирается на дугу АС, а значит равен ее половине.
∠ABC = 30° / 2 = 15°
Ответ: 15
5608FB
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 9°. Ответ дайте в градусах.
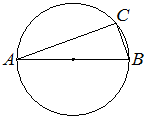
Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 9° = 81°
Ответ: 81
3561BE
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 44°. Ответ дайте в градусах.
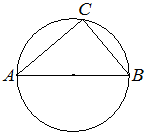
Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 44° = 46°
Ответ: 46
9F8E45
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 24°. Ответ дайте в градусах.

Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 24° = 66°
Ответ: 66
AF2B19
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.

Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 30° - 90° = 60°
Ответ: 60
FE3D40
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 33°. Ответ дайте в градусах.

Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 33° = 57°
Ответ: 57
4306BF
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 74°. Ответ дайте в градусах.

Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 74° = 16°
Ответ: 16
2A7231
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 48°. Ответ дайте в градусах.

Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 48° = 42°
Ответ: 42
36955E
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 17°. Ответ дайте в градусах.

Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 17° = 73°
Ответ: 73
D41B33
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 53°. Ответ дайте в градусах.

Решение:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 53° = 37°
Ответ: 37
AC3FA1
Найти угол трапеции
Один из углов равнобедренной трапеции равен 66°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 66° = 114°.
Ответ: 114
72397A

Один из углов равнобедренной трапеции равен 55°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 55° = 125°.
Ответ: 125
83A912

Один из углов равнобедренной трапеции равен 43°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 43° = 137°.
Ответ: 137
169635

Один из углов равнобедренной трапеции равен 74°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 74° = 106°.
Ответ: 106
3F0881

Один из углов равнобедренной трапеции равен 29°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 29° = 151°.
Ответ: 151
E13DF9

Один из углов равнобедренной трапеции равен 99°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то меньший угол в трапеции
180° - 99° = 81°.
Ответ: 81
AA4721

Один из углов равнобедренной трапеции равен 108°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то меньший угол в трапеции
180° - 108° = 72°.
Ответ: 72
E30CD4

Один из углов равнобедренной трапеции равен 94°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то меньший угол в трапеции
180° - 94° = 86°.
Ответ: 86
559F61

Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то меньший угол в трапеции
180° - 113° = 67°.
Ответ: 67
30C063

Один из углов равнобедренной трапеции равен 131°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то меньший угол в трапеции
180° - 131° = 49°.
Ответ: 49
EFEB4B
Один из углов прямоугольной трапеции равен 64°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение 2-мя способами:
Поскольку трапеция является прямоугольной, больший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 64° = 116°.
Ответ: 116
2 способ
Сумма углов в трапеции равна 360°, значит, больший угол равен 360° - 90° - 90° - 64° = 116°.
Ответ: 116.
4F5745

Один из углов прямоугольной трапеции равен 51°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, больший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 51° = 129°.
Ответ: 129
B68C17

Один из углов прямоугольной трапеции равен 82°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, больший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 82° = 98°.
Ответ: 98
109DA1

Один из углов прямоугольной трапеции равен 37°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, больший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 37° = 143°.
Ответ: 143
C0017A

Один из углов прямоугольной трапеции равен 72°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, больший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 72° = 108°.
Ответ: 108
0B6487

Один из углов прямоугольной трапеции равен 107°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, меньший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 107° = 73°.
Ответ: 73
7E48AD

Один из углов прямоугольной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, меньший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 113° = 67°.
Ответ: 67
6F62C1

Один из углов прямоугольной трапеции равен 102°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, меньший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 102° = 78°.
Ответ: 78
4C0223

Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, меньший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 121° = 59°.
Ответ: 59
2D6020

Один из углов прямоугольной трапеции равен 139°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Поскольку трапеция является прямоугольной, меньший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 139° = 41°.
Ответ: 41
F22DB9
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
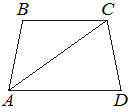
Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 46° - 1° = 133°.
Ответ: 133
2 способ рассуждения
∠ВАD = ∠САD + ∠BAC = 46° + 1° = 47°
По свойству равнобедренной трапеции, углы при основании равны.
Так как ∠ВАD получился острым, то ∠ABC=∠ВСD - тупые, это и есть наибольшие углы трапеции.
AD||BC (по определению трапеции), следовательно боковую сторону AB можно рассматривать как секущую,
а сумма односторонних углов (углы при параллельных прямых и секущей) равна 180°, значит
∠ABC= 180° - ∠ВАD = 180° - 47° = 133°
Ответ: 133
AA289E
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 33° и 13° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 33° - 13° = 134°.
Ответ: 134
C24770
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 62° и 9° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 62° - 9° = 109°.
Ответ: 109
03ADBA
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 12° и 13° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 12° - 13° = 155°.
Ответ: 155
196299
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 17° и 23° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 17° - 23° = 140°.
Ответ: 140
9E3839
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 11° и 60° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 11° - 60° = 109°.
Ответ: 109
0C516B
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 36° и 53° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 36° - 53° = 91°.
Ответ: 91
CEA572
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 47° и 15° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 47° - 15° = 118°.
Ответ: 118
A02E22
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 19° и 54° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 19° - 54° = 107°.
Ответ: 107
BE7D99
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 4° и 68° соответственно. Ответ дайте в градусах.

Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 4° - 68° = °.
Ответ:
5F541E
В трапеции ABCD известно, что AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
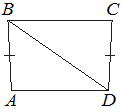
Решение:
∠ADC = ∠BDA + ∠BDC = 35° + 58° = 93°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC=93°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BDA - ∠BAD
∠ABD = 180° - 93° - 35°
∠ABD = 52°
Ответ: 52
C99939
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
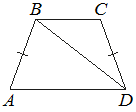
Решение:
∠ADC = ∠BDA + ∠BDC = 38° + 32° = 70°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 70°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 70° - 38° = 72°
Ответ: 72
A40158
В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=24°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠ADC = ∠BDA + ∠BDC = 40° + 24° = 64°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 64°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 64° - 40° = 76°
Ответ: 76
89D0DC
В трапеции ABCD известно, что AB=CD, ∠BDA=30° и ∠BDC=110°. Найдите угол ABD. Ответ дайте в градусах.
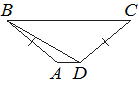
Решение:
∠ADC = ∠BDA + ∠BDC = 30° + 110° = 140°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 140°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 140° - 30° = 10°
Ответ: 10
9D6133
В трапеции ABCD известно, что AB=CD, ∠BDA=14° и ∠BDC=106°. Найдите угол ABD. Ответ дайте в градусах.
Решение:
∠ADC = ∠BDA + ∠BDC = 14° + 106° = 120°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 120°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 120° - 14° = 46°
Ответ: 46
F85286
В трапеции ABCD известно, что AB=CD, ∠BDA=24° и ∠BDC=70°. Найдите угол ABD. Ответ дайте в градусах.
Решение:
∠ADC = ∠BDA + ∠BDC = 24° + 70° = 94°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 94°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 94° - 24° = 62°
Ответ: 62
6D48C8
В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.
Решение:
∠ADC = ∠BDA + ∠BDC = 54° + 33° = 87°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 87°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 87° - 54° = 39°
Ответ: 39
EE98DF
В трапеции ABCD известно, что AB=CD, ∠BDA=22° и ∠BDC=45°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠ADC = ∠BDA + ∠BDC = 22° + 45° = 67°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 67°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 67° - 22° = 91°
Ответ: 91
937433
В трапеции ABCD известно, что AB=CD, ∠BDA=67° и ∠BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
Решение:
∠ADC = ∠BDA + ∠BDC = 67° + 28° = 95°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 95°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 95° - 67° = 18°
Ответ: 18
65F68A
В трапеции ABCD известно, что AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
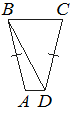
Решение:
∠ADC = ∠BDA + ∠BDC = 62° + 42° = 104°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 104°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 104° - 62° = 14°
Ответ: 14
740134
В трапеции ABCD известно, что AB=CD, ∠BDA=18° и ∠BDC=97°. Найдите угол ABD. Ответ дайте в градусах.
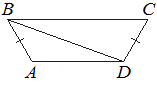
Решение:
∠ADC = ∠BDA + ∠BDC = 18° + 97° = 115°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 115°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 115° - 18° = 47°
Ответ: 47
E44CDE
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
50° / 2 = 25°.
Сумма односторонних углов трапеции равна 180°, поэтому больший угол равен
180° − 25° = 155°.
Ответ: 155
2AD397
Сумма двух углов равнобедренной трапеции равна 102°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
102° / 2 = 51°.
Сумма односторонних углов трапеции равна 180°, поэтому больший угол равен
180° − 51° = 129°.
Ответ: 129
51D937
Сумма двух углов равнобедренной трапеции равна 46°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
46° / 2 = 23°.
Сумма односторонних углов трапеции равна 180°, поэтому больший угол равен
180° − 23° = 157°.
Ответ: 157
F489B6
Сумма двух углов равнобедренной трапеции равна 178°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
178° / 2 = 89°.
Сумма односторонних углов трапеции равна 180°, поэтому больший угол равен
180° − 89° = 91°.
Ответ: 91
E677A3
Сумма двух углов равнобедренной трапеции равна 94°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
94° / 2 = 47°.
Сумма односторонних углов трапеции равна 180°, поэтому больший угол равен
180° − 47° = 133°.
Ответ: 133
B5FC63
Сумма двух углов равнобедренной трапеции равна 218°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
218° / 2 = 109°.
Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен
180° − 109° = 71°.
Ответ: 71
135ADE
Сумма двух углов равнобедренной трапеции равна 268°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
268° / 2 = 134°.
Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен
180° − 134° = 46°.
Ответ: 46
C1A434
Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
220° / 2 = 110°.
Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен
180° − 110° = 70°.
Ответ: 70
799B93
Сумма двух углов равнобедренной трапеции равна 196°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
196° / 2 = 98°.
Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен
180° − 98° = 82°.
Ответ: 82
3A1E7F
Сумма двух углов равнобедренной трапеции равна 352°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
352° / 2 = 176°.
Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен
180° − 176° = 4°.
Ответ: 4
79C6CA
Найти угол параллелограмма
Один из углов параллелограмма равен 41°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 41° = 139°.
Ответ: 139
B072E0

Один из углов параллелограмма равен 61°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 61° = 119°.
Ответ: 119
D774E6

Один из углов параллелограмма равен 33°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 33° = 147°.
Ответ: 147
488431

Один из углов параллелограмма равен 74°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 74° = 106°.
Ответ: 106
9327FE

Один из углов параллелограмма равен 26°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 26° = 154°.
Ответ: 154
9AF89A

Один из углов параллелограмма равен 96°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 96° = 84°.
Ответ: 84
AAF3C7

Один из углов параллелограмма равен 102°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 102° = 78°.
Ответ: 78
6D6AD2

Один из углов параллелограмма равен 91°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 91° = 89°.
Ответ: 89
79590F

Один из углов параллелограмма равен 111°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 111° = 69°.
Ответ: 69
72C87D

Один из углов параллелограмма равен 128°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 128° = 52°.
Ответ: 52
8AB667
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
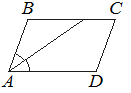
Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 15 = 30°.
Этот угол является острым углом параллелограмма.
Ответ: 30
466CCD
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 33 = 66°.
Этот угол является острым углом параллелограмма.
Ответ: 66
E13348
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 41 = 82°.
Этот угол является острым углом параллелограмма.
Ответ: 82
4B3FF8
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 44°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 44 = 88°.
Этот угол является острым углом параллелограмма.
Ответ: 88
0B7B91
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 40°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 40 = 80°.
Этот угол является острым углом параллелограмма.
Ответ: 80
B16663
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 34°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 34 = 68°.
Этот угол является острым углом параллелограмма.
Ответ: 68
CBFC2D
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 16°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 16 = 32°.
Этот угол является острым углом параллелограмма.
Ответ: 32
0ACA8D
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 9°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 9 = 18°.
Этот угол является острым углом параллелограмма.
Ответ: 18
2EAA56
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 12°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 12 = 24°.
Этот угол является острым углом параллелограмма.
Ответ: 24
95389D
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 8°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 8 = 16°.
Этот угол является острым углом параллелограмма.
Ответ: 16
BF5E8F
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 21°. Ответ дайте в градусах.

Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 21 = 42°.
Этот угол является острым углом параллелограмма.
Ответ: 42
735F1A
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
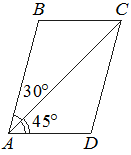
Решение 2-мя способами:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠АDС — больший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Рассмотрим треугольник АВС.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BAC - ∠BCA = 180° - 30° - 45° = 105°.
Ответ: 105
2 способ рассуждения
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠АDС — больший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно сторону AВ можно рассматривать как секущую.
Углы ВАD и АВС односторонние, значит их сумма равна 180° .
∠ВАD = ∠BAC + ∠САD
Отсюда:
∠ABC= 180° - ∠ВАD = 180° - ∠BAC - ∠BCA = 180° - 30° - 45° = 105°.
Ответ: 105
7C57E0
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
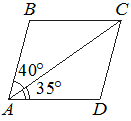
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠АDС — больший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Рассмотрим треугольник АВС.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BAC - ∠BCA = 180° - 40° - 35° = 105°.
Ответ: 105
4A48AF
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.

Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠BAD=∠ВСD — меньший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ ВD можно рассматривать как секущую при параллельных прямых,
углы CВD и АDВ равны как накрест лежащие:
∠АDВ = ∠CВD
Рассмотрим треугольник АВD.
Сумма углов треугольника равна 180°. Отсюда:
∠ВАD = 180° - ∠АВD - ∠АDВ = 180° - ∠АВD - ∠CВD = 180° - 50° - 85° = 45°.
Ответ: 45
1520BE
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
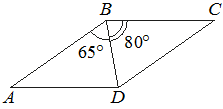
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠BAD=∠ВСD — меньший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ ВD можно рассматривать как секущую при параллельных прямых,
углы CВD и АDВ равны как накрест лежащие:
∠АDВ = ∠CВD
Рассмотрим треугольник АВD.
Сумма углов треугольника равна 180°. Отсюда:
∠ВАD = 180° - ∠АВD - ∠АDВ = 180° - ∠АВD - ∠CВD = 180° - 65° - 80° = 35°.
Ответ: 35
095900
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
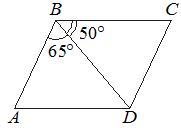
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠BAD=∠ВСD — меньший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ ВD можно рассматривать как секущую при параллельных прямых,
углы CВD и АDВ равны как накрест лежащие:
∠АDВ = ∠CВD
Рассмотрим треугольник АВD.
Сумма углов треугольника равна 180°. Отсюда:
∠ВАD = 180° - ∠АВD - ∠АDВ = 180° - ∠АВD - ∠CВD = 180° - 65° - 50° = 65°.
Ответ: 65
0E2BF9
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
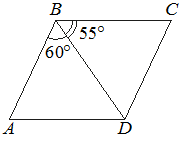
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠BAD=∠ВСD — меньший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ ВD можно рассматривать как секущую при параллельных прямых,
углы CВD и АDВ равны как накрест лежащие:
∠АDВ = ∠CВD
Рассмотрим треугольник АВD.
Сумма углов треугольника равна 180°. Отсюда:
∠ВАD = 180° - ∠АВD - ∠АDВ = 180° - ∠АВD - ∠CВD = 180° - 60° - 55° = 65°.
Ответ: 65
CE33E8
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
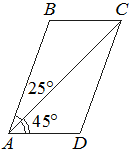
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠АDС — больший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Рассмотрим треугольник АВС.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BAC - ∠BCA = 180° - 45° - 25° = 110°.
Ответ: 110
AB5A83
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
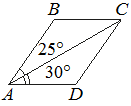
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠АDС — больший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Рассмотрим треугольник АВС.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BAC - ∠BCA = 180° - 25° - 30° = 125°.
Ответ: 125
E63248
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
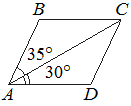
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠АDС — больший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Рассмотрим треугольник АВС.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BAC - ∠BCA = 180° - 35° - 30° = 115°.
Ответ: 115
8F3B36
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
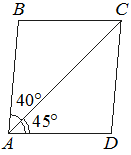
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠АDС — больший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Рассмотрим треугольник АВС.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BAC - ∠BCA = 180° - 45° - 40° = 95°.
Ответ: 95
32151E
Найти угол ромба
Один из углов ромба равен 43°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 43° = 137°.
Ответ: 137
B30F7F

Один из углов ромба равен 62°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 62° = 118°.
Ответ: 118
1D1310

Один из углов ромба равен 35°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 35° = 145°.
Ответ: 145
151F75

Один из углов ромба равен 76°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 76° = 104°.
Ответ: 104
F547A6

Один из углов ромба равен 24°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 24° = 156°.
Ответ: 156
83689C

Один из углов ромба равен 99°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 99° = 81°.
Ответ: 81
C764EF

Один из углов ромба равен 104°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 104° = 76°.
Ответ: 76
D4E3E6

Один из углов ромба равен 93°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 93° = 87°.
Ответ: 87
8BEE54

Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 114° = 66°.
Ответ: 66
F45E6B

Один из углов ромба равен 127°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда меньший угол равен
180° - 127° = 53°.
Ответ: 53
365266
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Решение 2-я способами:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 72° = 108°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 108° / 2 = 54°.
Ответ: 54
2 способ для тех, кто забыл свойства диагонали ромба
По определению ромба все его стороны равны. Тогда треугольник АВС равнобедренный (ВС=ВА), а значит углы при основании равны. Сумма углов треугольника равна 180°. Отсюда
∠ВСА = (180° - ∠ABC) / 2 = (180° - 72°) / 2 = 54°
ВС||АD, а СА - секущая, значит ∠ВСА = ∠САD = 54° как накрест лежащие.
Треугольник АDС так же равнобедренный (СD=АD), значит
∠ACD = ∠САD = 54°
Ответ: 54
584A28

В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 40° = 140°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 140° / 2 = 70°.
Ответ: 70
B0B1CC

В ромбе ABCD угол ABC равен 84°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 84° = 96°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 96° / 2 = 48°.
Ответ: 48
9764FC

В ромбе ABCD угол ABC равен 82°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 82° = 98°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 98° / 2 = 49°.
Ответ: 49
021B92

В ромбе ABCD угол ABC равен 48°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 48° = 132°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 132° / 2 = 66°.
Ответ: 66
E84DB4

В ромбе ABCD угол ABC равен 56°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 56° = 124°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 124° / 2 = 62°.
Ответ: 62
508D62
В ромбе ABCD угол ABC равен 102°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 102° = 78°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 78° / 2 = 39°.
Ответ: 39
3310E3

В ромбе ABCD угол ABC равен 156°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 156° = 24°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 24° / 2 = 12°.
Ответ: 12
703153

В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 146° = 34°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 34° / 2 = 17°.
Ответ: 17
C42955

В ромбе ABCD угол ABC равен 134°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 134° = 46°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 46° / 2 = 23°.
Ответ: 23
3E3F85
Найти угол между диагоналями прямоугольника
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 50° = 80° - острый угол
Ответ: 80
6E783C
Диагональ прямоугольника образует угол 44° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Обратите внимание, по алгоритму угол находится тупой, требуются еще действия, в отличие от предыдущих задач такого типа!

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 44° = 92° - тупой угол
Сумма смежных углов, которые образуют пересекающиеся диагонали, равна 180°, значит острый угол равен
180° - 92° = 88°
Ответ: 88
C70802
Диагональ прямоугольника образует угол 86° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 86° = 8° - острый угол
Ответ: 8
06DA84
Диагональ прямоугольника образует угол 70° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 70° = 40° - острый угол
Ответ: 40
CA87B1
Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 47° = 86° - острый угол
Ответ: 86
29E2E9
Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 51° = 78° - острый угол
Ответ: 78
9C43F6
Диагональ прямоугольника образует угол 63° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 63° = 54° - острый угол
Ответ: 54
2FCAE5
Диагональ прямоугольника образует угол 65° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 65° = 50° - острый угол
Ответ: 50
1632B0
Диагональ прямоугольника образует угол 74° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 74° = 32° - острый угол
Ответ: 32
17061A
Диагональ прямоугольника образует угол 61° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 61° = 58° - острый угол
Ответ: 58
84D692