Ответы к странице 187
770. Какой из графиков, представленных на рисунке 43, является графиком движения пешехода, который шел с постоянной скоростью? Определите скорость движения этого пешехода.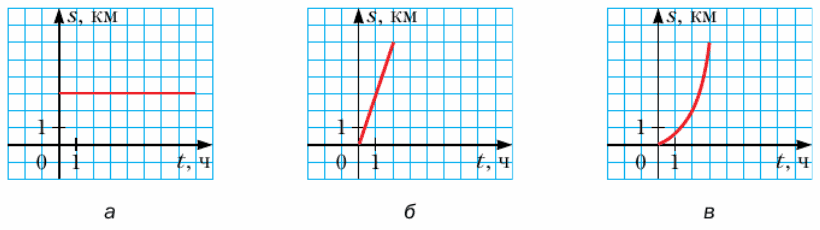
Решение:
График б является графиком движения пешехода, который шел с постоянной скоростью.
Так как, одна клетка соответствует одному пройденному километру, то пешеход за 1 час прошел 2 километра. Следовательно скорость пешехода 2 км/ч.
Ответ: график б; 2 км/ч.
771. Смешали 2 л молока жирностью 8% и 3 л молока жирностью 6%. Какова жирность полученной смеси?
Решение:
8% − это 0,08
6% − это 0,06
1) 2 * 0,08 = 0,16 (л) − жира содержится в 2 литрах молока 8%;
2) 3 * 0,06 = 0,18 (л) − жира содержится в 3 литрах молока 6%;
3) 2 + 3 = 5 (л) − смеси получилось всего;
4) 0,16 + 0,18 = 0,34 (л) − жира получилось всего в смеси;
5) $\frac{0,34}{5} * 100$% = 0,34 * 20% = 6,8% − жирность полученной смеси.
Ответ: 6,8%
772. Решите уравнение:
1) $x^2 = 9$;
2) $x^2 = -9$;
3) $(4x + 1)^2 = 9$;
4) $(x - 1)^2 = 5$;
5) $\sqrt{x} = 9$;
6) $\sqrt{x} = -9$.
Решение:
1) $x^2 = 9$
x = ±3
Ответ: x = −3 и x = 3
2) $x^2 = -9$
Ответ: нет корней
3) $(4x + 1)^2 = 9$
4x + 1 = 3
4x = 3 − 1
4x = 2
x = 0,5
или
4x + 1 = −3
4x = −3 − 1
4x = −4
x = −1
Ответ: x = −1 и x = 0,5
4) $(x - 1)^2 = 5$
$x - 1 = \sqrt{5}$
$x = \sqrt{5} + 1$
или
$x - 1 = -\sqrt{5}$
$x = 1 - \sqrt{5}$
Ответ: $x = 1 - \sqrt{5}$ и $x = \sqrt{5} + 1$
5) $\sqrt{x} = 9$
$(\sqrt{x})^2 = 9^2$
x = 81
Ответ: x = 81
6) $\sqrt{x} = -9$
Ответ: нет корней
773. Решите уравнение:
1) $\frac{4x - 1}{x - 2} = \frac{x + 5}{x - 2}$;
2) $\frac{2y^2 - 3y - 20}{y - 4} - y = 1$;
3) $\frac{5x - 3}{x + 1} - \frac{4x - 2}{x + 2} = 1$;
4) $\frac{1}{y - 5} - \frac{1}{y + 4} = \frac{9}{(y - 5)(y + 4)}$.
Решение:
1) $\frac{4x - 1}{x - 2} = \frac{x + 5}{x - 2}$
x − 2 ≠ 0
x ≠ 2
4x − 1 = x + 5
4x − x = 5 + 1
3x = 6
x = 2 − не может быть корнем, так как в знаменателе будет 0.
Ответ: нет корней
2) $\frac{2y^2 - 3y - 20}{y - 4} - y = 1$
y − 4 ≠ 0
y ≠ 4
$\frac{2y^2 - 3y - 20}{y - 4} - y = 1$| * (y − 4)
$2y^2 - 3y - 20 - y(y - 4) = y - 4$
$2y^2 - 3y - 20 - y^2 + 4y - y + 4 = 0$
$y^2 - 16 = 0$
$y^2 = 16$
$y_1 = 4$ − не может быть корнем, так как в знаменателе будет 0.
$y_2 = -4$
Ответ: y = −4
3) $\frac{5x - 3}{x + 1} - \frac{4x - 2}{x + 2} = 1$
x + 1 ≠ 0
x ≠ −1
и
x + 2 ≠ 0
x ≠ −2
$\frac{5x - 3}{x + 1} - \frac{4x - 2}{x + 2} = 1$ | * (x + 1)(x + 2)
(5x − 3)(x + 2) − (4x − 2)(x + 1) = (x + 1)(x + 2)
$5x^2 - 3x + 10x - 6 - (4x^2 - 2x + 4x - 2) = x^2 + x + 2x + 2$
$5x^2 + 7x - 6 - 4x^2 - 2x + 2 = x^2 + 3x + 2$
$x^2 + 5x - 4 - x^2 - 3x - 2 = 0$
2x − 6 = 0
2x = 6
x = 3
Ответ: x = 3
4) $\frac{1}{y - 5} - \frac{1}{y + 4} = \frac{9}{(y - 5)(y + 4)}$
y − 5 ≠ 0
y ≠ 5
и
y + 4 ≠ 0
y ≠ −4
$\frac{1}{y - 5} - \frac{1}{y + 4} = \frac{9}{(y - 5)(y + 4)}$ I * (y − 5)(y + 4)
y + 4 − (y − 5) = 9
y + 4 − y + 5 = 9
y − y = 9 − 5 − 4
0 = 0
Ответ: y − любое число, кроме y = 5 и y = −4.
№774. Рассматриваются все прямоугольники, длины сторон которых − натуральные числа. Каких прямоугольников больше: с периметром 1000 или с периметром 1002?
Решение:
Длина наименьшей стороны прямоугольника с периметром 1000 может быть любым натуральным числом от 1 до 1000 : 4 = 250.
Такие же значения может принимать длина наименьшей стороны прямоугольника с периметром 1002.
Таким образом, между множеством прямоугольников с периметром 1000 и множеством прямоугольников с периметром 1002 можно установить взаимно однозначное соответствие.
Ответ: одинаковое количество.

