Ответы к странице 85-86
Задание №3 "Проверьте себя" в тестовой форме
1. Решите уравнение:
$\frac{x^2 - 100}{x - 10} = 0$
А) −10; 10
Б) 10
В) −10
Г) корней нет
Решение:
$\frac{x^2 - 100}{x - 10} = 0$
x − 10 ≠ 0
x ≠ 10
$x^2 - 100 = 0$
$x^2 = 100$
x = 10 − не подходит
x = −10
Ответ: В) −10
2. Решите уравнение:
$\frac{x - 10}{x^2 - 100} = 0$
А) −10; 10
Б) 10
В) −10
Г) корней нет
Решение:
$\frac{x - 10}{x^2 - 100} = 0$
$x^2 - 100 ≠ 0$
$x^2 ≠ 100$
x ≠ ±10
x − 10 = 0
x = 10 − не подходит
Ответ: Г) корней нет
3. Какое из данных равенств верно?
А) $10^{-3} = -1000$
Б) $(-1\frac{1}{3})^{-2} = -\frac{9}{16}$
В) $(-2)^{-3} = -\frac{1}{8}$
Г) $\frac{1}{7^{-2}} = -49$
Решение:
А)
$10^{-3} = -1000$
$\frac{1}{10^3} = -1000$
$\frac{1}{1000} = -1000$ − неверно
Б)
$(-1\frac{1}{3})^{-2} = -\frac{9}{16}$
$(-\frac{4}{3})^{-2} = -\frac{9}{16}$
$(-\frac{3}{4})^{2} = -\frac{9}{16}$
$\frac{9}{16} = -\frac{9}{16}$ − неверно
В)
$(-2)^{-3} = -\frac{1}{8}$
$(-\frac{1}{2})^{3} = -\frac{1}{8}$
$-\frac{1}{8} = -\frac{1}{8}$ − верно
Г)
$\frac{1}{7^{-2}} = -49$
$7^2 = -49$
49 = −49 − неверно
Ответ: В) $(-2)^{-3} = -\frac{1}{8}$
4. Как записывают в стандартном виде число 42000?
А) $4,2 * 10^3$
Б) $4,2 * 10^4$
В) $0,42 * 10^5$
Г) $42 * 10^3$
Решение:
$4,2 * 10000 = 4,2 * 10^4$
Ответ: Б) $4,2 * 10^4$
5. Как записывают в виде десятичной дроби число $6,3 * 10^{-3}$?
А) 0,63
Б) 0,063
В) 0,0063
Г) 0,00063
Решение:
$6,3 * 10^{-3} = 6,3 * \frac{1}{10^3} = 6,3 * \frac{1}{1000} = 0,0063$
Ответ: В) 0,0063
6. Представьте число $\frac{1}{25}$ в виде степени с основанием 5.
А) $5^{-2}$
Б) $5^{2}$
В) $5^{-3}$
Г) $5^{3}$
Решение:
$\frac{1}{25} = \frac{1}{5^2} = 5^{-2}$
Ответ: А) $5^{-2}$
7. Чему равно значение выражения
$(1,7 * 10^8) * (6 * 10^{-3})$?
А) $1,02 * 10^5$
Б) $1,02 * 10^6$
В) $10,2 * 10^6$
Г) $1,02 * 10^7$
Решение:
$(1,7 * 10^8) * (6 * 10^{-3}) = (1,7 * 6) * (10^8 * 10^{-3}) = 10,2 * 10^{8 - 3} = 10,2 * 10^5 = 1,02 * 10^6$
Ответ: Б) $1,02 * 10^6$
8. Найдите значение выражения $\frac{9^{-2} * 3^{-5}}{81 * 27^{-3}}$.
А) 81
Б) $\frac{1}{81}$
В) 27
Г) $\frac{1}{27}$
Решение:
$\frac{9^{-2} * 3^{-5}}{81 * 27^{-3}} = \frac{(3^2)^{-2} * 3^{-5}}{3^4 * (3^3)^{-3}} = \frac{3^{-4} * 3^{-5}}{3^4 * 3^{-9}} = \frac{3^{-9}}{3^{-5}} = 3^{-9 - (-5)} = 3^{-9 + 5} = 3^{-4} = \frac{1}{3^4} = \frac{1}{81}$
Ответ: Б) $\frac{1}{81}$
9. Какая из данных функций не является обратной пропорциональностью?
А) $y = \frac{3}{x}$
Б) $y = -\frac{3}{x}$
В) $y = \frac{3}{2x}$
Г) $y = \frac{3x}{2}$
Решение:
Обратной пропорциональностью не является функция $y = \frac{3x}{2}$
Ответ: Г) $y = \frac{3x}{2}$
10. На одном из рисунков изображен график функции $y = -\frac{4}{x}$. Укажите этот рисунок.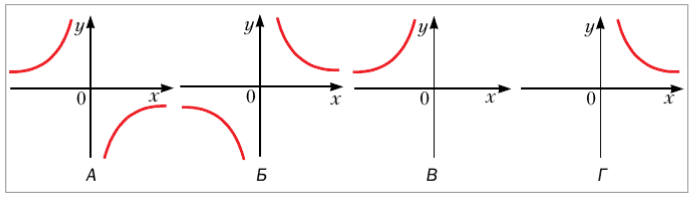
Решение:
График функции $y = -\frac{4}{x}$ является гиперболой и расположен во II и IV четвертях
Ответ: А
11. При каком значении k график функции $y = \frac{k}{x}$ проходит через точку A(−3; 0,6)?
А) −1,8
Б) −0,2
В) −2,4
Г) −3,6
Решение:
$y = \frac{k}{x}$
A(−3; 0,6)
$0,6 = \frac{k}{-3}$
k = −3 * 0,6
k = −1,8
Ответ: А) −1,8
12. Решите уравнение $\frac{2x - 1}{x + 4} - \frac{3x + 1}{4 - x} = \frac{4x^2 + 8}{x^2 - 16}$.
А) 0; 4
Б) −4; 0
В) −4
Г) 0
Решение:
$\frac{2x - 1}{x + 4} - \frac{3x + 1}{4 - x} = \frac{4x^2 + 8}{x^2 - 16}$
$\frac{2x - 1}{x + 4} + \frac{3x + 1}{x - 4} = \frac{4x^2 + 8}{(x - 4)(x + 4)}$
x + 4 ≠ 0
x ≠ −4
и
x − 4 ≠ 0
x ≠ 4
$\frac{(2x - 1)(x - 4) + (3x + 1)(x + 4)}{(x - 4)(x + 4)} = \frac{4x^2 + 8}{(x - 4)(x + 4)} |* (x - 4)(x + 4)$
$2x^2 - x - 8x + 4 + 3x^2 + x + 12x + 4 = 4x^2 + 8$
$5x^2 + 4x + 8 - 4x^2 - 8 = 0$
$x^2 + 4x = 0$
x(x + 4) = 0
x = 0
или
x + 4 = 0
x = −4 − не подходит
Ответ: Г) 0

