Ответы к странице 94

368. Докажите тождество:
$\frac{(a + b)^2}{a - b} : (\frac{a}{a - b} + \frac{a^2 + b^2}{a^2 - b^2} - \frac{a}{a + b}) = a + b$

Решение:

$\frac{(a + b)^2}{a - b} : (\frac{a}{a - b} + \frac{a^2 + b^2}{a^2 - b^2} - \frac{a}{a + b}) = \frac{(a + b)^2}{a - b} : (\frac{a}{a - b} + \frac{a^2 + b^2}{(a - b)(a + b)} - \frac{a}{a + b}) = \frac{(a + b)^2}{a - b} : \frac{a(a + b)+ a^2 + b^2 - a(a - b)}{(a - b)(a + b)} = \frac{(a + b)^2}{a - b} : \frac{a^2 + ab+ a^2 + b^2 - a^2 + ab}{(a - b)(a + b)} = \frac{(a + b)^2}{a - b} : \frac{a^2 + 2ab + b^2}{(a - b)(a + b)} = \frac{(a + b)^2}{a - b} * \frac{(a - b)(a + b)}{(a + b)^2} = a + b$

369. Решите уравнение:
$\frac{6}{x - 2} - \frac{x + 3}{x} = \frac{x + 6}{x^2 - 2x}$

Решение:

$\frac{6}{x - 2} - \frac{x + 3}{x} = \frac{x + 6}{x^2 - 2x}$
x − 2 ≠ 0
x ≠ 2
x ≠ 0
$\frac{6}{x - 2} - \frac{x + 3}{x} = \frac{x + 6}{x^2 - 2x}$
$\frac{6x - (x + 3)(x - 2)}{x(x - 2)} = \frac{x + 6}{x(x - 2)} |* x(x - 2)$
$6x - (x^2 + 3x - 2x - 6) = x + 6$
$6x - (x^2 + x - 6) = x + 6$
$6x - x^2 - x + 6 - x - 6 = 0$
$4x - x^2 = 0$
x(4 − x) = 0
x = 0 − не подходит
или
4 − x = 0
x = 4
Ответ: x = 4

370. Докажите, что значение выражения $27^6 - 9^7$ кратно 48.

Решение:

$27^6 - 9^7 = (3^3)^6 - (3^2)^7 = 3^{18} - 3^{14} = 3^{14}(3^4- 1) = 3^{14} * 80 = (3 * 3^{13}) * (5 * 16) = (3 * 16) * (3^{13} * 5) = 48 * (3^{13} * 5)$
Так как в произведении один из множителей равен 48, значит значение выражения кратно 48.

371. Из двух пунктов, расстояние между которыми равно 30 км, одновременно навстречу друг другу вышли два туриста и встретились через 3 ч 45 мин. Если бы первый из них вышел на 2 ч раньше второго, то они встретились бы через 4,5 ч после выхода первого. Найдите скорость каждого туриста.

Решение:

3 ч 45 мин = $3\frac{45}{60}$ ч = $3\frac{3}{4}$ ч = 3,75 ч
Пусть:
x (км/ч) − скорость первого туриста;
y (км/ч) − скорость второго туриста.
В первом случае каждый из туристов двигался 3,75 ч, тогда:
3,75x (км) − пройдет за 3 ч 45 мин первый турист;
3,75y (км) − пройдет за 3 ч 45 мин второй турист.
Так как суммарно туристы пройдут 30 км, можно составить уравнение:
3,75x + 3,75y = 30

Во втором случае первый турист двигался 4,5 ч, значит:
4,5 − 2 = 2,5 (ч) − двигался второй турист;
4,5x (км) − пройдет за 4,5 ч первый турист;
2,5y (км) − пройдет за 2 ч второй турист.
Так как суммарно туристы пройдут 30 км, можно составить уравнение:
4,5x + 2,5y = 30

Составим систему уравнений:
$\begin{equation*} \begin{cases} 3,75x + 3,75y = 30 |* 4 &\\ 4,5x + 2,5y = 30 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} 15x + 15y = 120 &\\ 4,5x + 2,5y = 30 |* 6 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} 15x + 15y = 120 &\\ 27x + 15y = 180 & \end{cases} \end{equation*}$
15x + 15y − (27x + 15y) = 120 − 180
15x + 15y − 27x − 15y = −60
−12x = −60
x = 5 (км/ч) − скорость первого туриста;
15x + 15y = 120
15 * 5 + 15y = 120
75 + 15y = 120
15y = 120 − 75
15y = 45
y = 3 (км/ч) − скорость второго туриста.
Ответ: 5 км/ч и 3 км/ч

372. Найдите сторону квадрата, площадь которого равна:
1) 25 $см^2$;
2) 1600 $дм^2$;
3) 0,04 $м^2$.

Решение:

1) Пусть a (см) − сторона квадрата, тогда:
$S = a^2$
$25 = a^2$
$a^2 - 25 = 0$
(a − 5)(a + 5) = 0
a − 5 = 0
a = 5
или
a + 5 = 0
a = −5 − не подходит, так как сторона квадрата не может быть числом отрицательным.
Ответ: 5 см

2) Пусть a дм − сторона квадрата, тогда
$S = a^2$
$1600 = a^2$
$a^2 - 1600 = 0$
(a − 40)(a + 40) = 0
a − 40 = 0
a = 40
или
a + 40 = 0
a = −40 − не подходит, так как сторона квадрата не может быть числом отрицательным.
Ответ: 40 дм

3) Пусть a (м) − сторона квадрата, тогда
$S = a^2$
$0,04 = a^2$
$a^2 - 0,04 = 0$
(a − 0,2)(a + 0,2) = 0
a − 0,2 = 0
a = 0,2
или
a + 0,2 = 0
a = −0,2 − не подходит, так как сторона квадрата не может быть числом отрицательным.
Ответ: 0,2 м

373. Решите уравнение:
1) $x^2 = 9$;
2) $x^2 = \frac{36}{49}$.

Решение:

1) $x^2 = 9$
$x^2 - 9 = 0$
(x − 3)(x + 3) = 0
x − 3 = 0
x = 3
или
x + 3 = 0
x = −3
Ответ: x = ±3

2) $x^2 = \frac{36}{49}$
$x^2 - \frac{36}{49} = 0$
$(x - \frac{6}{7})(x + \frac{6}{7}) = 0$
$x - \frac{6}{7} = 0$
$x = \frac{6}{7}$
или
$x + \frac{6}{7} = 0$
$x = -\frac{6}{7}$
Ответ: $x = ±\frac{6}{7}$

374. При каких значениях a уравнение $x^2 = a$ не имеет корней?

Решение:

Так как $x^2 ≥ 0$, то уравнение $x^2 = a$ не имеет корней при a < 0.

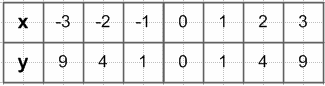
375. Постройте графики функций $y = x^2$ и y = 1 и найдите координаты их общих точек.

Решение:

$y = x^2$ − парабола

y = 1 − прямая

Ответ: (−1;1) и (1;1) − координаты общих точек.

№376. Натуральные числа x, y, z таковы, что значения выражений x + y, y + z, x + z − простые числа. Докажите, что среди чисел x, y, z есть по крайней мере два числа, равные 1.

Решение:

Все простые числа, кроме числа 2, нечетные.
Представим, что среди чисел x, y, z нет двух чисел равных 1, значит каждая из сумм будет больше 2, а значит будет числом нечетным.
Чтобы в сумме получить нечетное число, одно из слагаемых должно быть числом четным, а второе нечетным.
Допустим:
x − четное число, тогда:
y − будет нечетным числом,
z − будет четным числом.
Тогда сумма x + z будет четным числом, а значит не будет простым числом.
Допустим:
x − нечетное число, тогда:
y − будет четным числом,
z − будет нечетным числом.
Тогда сумма x + z будет четным числом, а значит не будет простым числом.
Поэтому, чтобы удовлетворялось условие задачи по крайней мере два числа должны быть равны 1.
Проверим, пусть:
x = 1, y = 1, тогда:
x + y = 2 − простое число;
z − может быть любым натуральным числом на 1 меньше любого простого, например 4 (5 − 1), тогда:
y + z = 1 + 4 = 5 − простое число;
x + z = 1 + 4 = 5 − простое число.