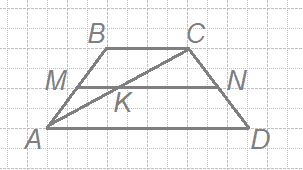Вспоминаем, что средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты. Еще нужно повторить теорему Фалеса: если параллельные прямые пересекают две данные прямые и отсекают на одной из них равные отрезки, то они отсекают равные отрезки и на другой данной прямой. В открытом банке заданий ФИПИ про среднюю линию трапеции есть следующие задания.
Реальные задания по геометрии из банка ФИПИ
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(3 + 9) / 2 = 6
Ответ: 6
20E8E9

Основания трапеции равны 4 и 6, а высота равна 4. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(4 + 6) / 2 = 5
Ответ: 5
E0C08E

Основания трапеции равны 2 и 12, а высота равна 6. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(2 + 12) / 2 = 7
Ответ: 7
1B181B

Основания трапеции равны 5 и 11, а высота равна 7. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(5 + 11) / 2 = 8
Ответ: 8
B23770

Основания трапеции равны 1 и 5, а высота равна 3. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(1 + 5) / 2 = 3
Ответ: 3
6F6044

Основания трапеции равны 4 и 14, а высота равна 8. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(4 + 14) / 2 = 9
Ответ: 9
0CC123

Основания трапеции равны 7 и 21, а высота равна 6. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(7 + 21) / 2 = 14
Ответ: 14
0996BF

Основания трапеции равны 8 и 18, а высота равна 5. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(8 + 18) / 2 = 13
Ответ: 13
5D3C40

Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(11 + 19) / 2 = 15
Ответ: 15
936640

Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(2 + 6) / 2 = 4
Ответ: 4
B72AA0
Основания трапеции равны 1 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 11/2 =5,5.
Ответ: 5,5.
98EEE4
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 11/2 =5,5.
Ответ: 5,5
8F7CEA
Основания трапеции равны 3 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 11/2 =5,5.
Ответ: 5,5
C432E5
Основания трапеции равны 8 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 17/2 =8,5.
Ответ: 8,5
7C9C1D
Основания трапеции равны 17 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 19/2 =9,5.
Ответ: 9,5
6F74CD
Основания трапеции равны 16 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 17/2 =8,5.
Ответ: 8,5
A11227
Основания трапеции равны 14 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 19/2 =9,5.
Ответ: 9,5
1C57C9
Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 17/2 =8,5.
Ответ: 8,5
8131F5
Основания трапеции равны 1 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 19/2 =9,5.
Ответ: 9,5
146E47
Основания трапеции равны 2 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 9/2 =4,5.
Ответ: 4,5
5ECD98