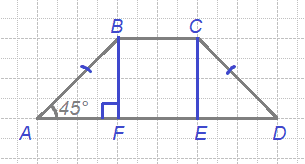
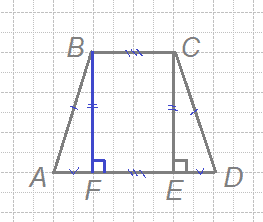Найдите основание трапеции. Задания ОГЭ по математике*

В следующих заданиях нужно найти основание трапеции, где-то большее, где-то меньшее, а в заданиях части 2 ОГЭ - оба. Вот что предлагает открытый банк заданий ФИПИ по этой теме.

Реальные задания по геометрии из банка ФИПИ

В равнобедренной трапеции известны высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.

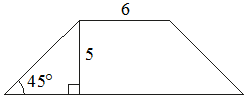
Решение:

Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ = 6
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
АD = АF + ЕD + FЕ = 2АF + FЕ = 2 * 5 + 6 = 16

Ответ: 16

D5D947

В равнобедренной трапеции известна высота, большее основание и угол при основании (см. рисунок). Найдите меньшее основание.

Решение:

Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
ВС = FЕ = АD - (АF + ЕD) = АD - 2АF = 15 - 2 * 5 = 5

Ответ: 5

EFBE26

В равнобедренной трапеции известна высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.

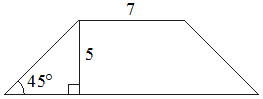
Решение:

Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ = 7
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
АD = АF + ЕD + FЕ = 2АF + FЕ = 2 * 5 + 7 = 17

Ответ: 17

33462D

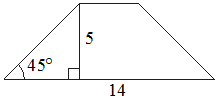
Решение:

Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
ВС = FЕ = АD - (АF + ЕD) = АD - 2АF = 14 - 2 * 5 = 4

Ответ: 4

C56952

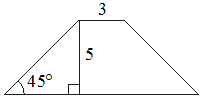
Решение:

Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ = 3
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
АD = АF + ЕD + FЕ = 2АF + FЕ = 2 * 5 + 3 = 13

Ответ: 13

99B09B

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания BC.

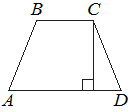
Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 8.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 15 - 8 = 7

Ответ: 7

267796

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 11. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 1.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 11 - 1 = 10

Ответ: 10

7FE0DC

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 10 и 11. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 10.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 11 - 10 = 1

Ответ: 1

DF571C

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 3 и 11. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 3.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 11 - 3 = 8

Ответ: 8

1F937D

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 17. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 8.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 17 - 8 = 9

Ответ: 9

54505A

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 17 и 19. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 17.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 19 - 17 = 2

Ответ: 2

4FA4EB

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 16 и 17. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 16.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 17 - 16 = 1

Ответ: 1

0A07C8

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 18. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 8.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 18 - 8 = 10

Ответ: 10

A6EA51

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 11 и 14. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 11.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 14 - 11 = 3

Ответ: 3

51BD7F

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 14 и 19. Найдите длину основания BC.

Решение:

Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 14.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 19 - 14 = 5

Ответ: 5

0BC157

Задания ОГЭ с развернутым ответом

Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.

Решение:

...
Ответ: ...

62EB73

Углы при одном из оснований трапеции равны 47° и 43°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 16 и 14. Найдите основания трапеции.

Решение:

...
Ответ: ...

9B51F6

Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 3. Найдите основания трапеции.

Решение:

...
Ответ: ...

7673A9

Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.

Решение:

...
Ответ: ...

AE4891

Углы при одном из оснований трапеции равны 53° и 37°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 2. Найдите основания трапеции.

Решение:

...
Ответ: ...

B9101E

Углы при одном из оснований трапеции равны 86° и 4°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 4 и 1. Найдите основания трапеции.

Решение:

...
Ответ: ...

BA70C1

Углы при одном из оснований трапеции равны 18° и 72°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 4. Найдите основания трапеции.

Решение:

...
Ответ: ...

ECF283

Углы при одном из оснований трапеции равны 80° и 10°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 20 и 17. Найдите основания трапеции.

Решение:

...
Ответ: ...

7B2FE8

Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 17. Найдите основания трапеции.

Решение:

...
Ответ: ...

84CE9A

Углы при одном из оснований трапеции равны 7° и 83°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 14 и 11. Найдите основания трапеции.

Решение:

...
Ответ: ...

C5871A