Задания про диагонали четырехугольников из открытого банка ФИПИ к ОГЭ по математике, которые могут вам попасться на реальном экзамене в этом году.
Реальные задания по геометрии из банка ФИПИ
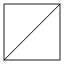
Сторона квадрата равна 7√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 7√2 = 7 * 2 = 14
Ответ: 14
40DFD2

Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 3√2 = 3 * 2 = 6
Ответ: 6
8C5C72

Сторона квадрата равна 2√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 2√2 = 2 * 2 = 4
Ответ: 4
D9A2FF

Сторона квадрата равна 10√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 10√2 = 10 * 2 = 20
Ответ: 20
2E2E14

Сторона квадрата равна 4√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 4√2 = 4 * 2 = 8
Ответ: 8
33F1C7

Сторона квадрата равна 5√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 5√2 = 5 * 2 = 10
Ответ: 10
55322A

Сторона квадрата равна 11√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 11√2 = 11 * 2 = 22
Ответ: 22
FA194C

Сторона квадрата равна 8√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 8√2 = 8 * 2 = 16
Ответ: 16
72FCEC

Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 9√2 = 9 * 2 = 18
Ответ: 18
C3668A

Сторона квадрата равна 6√2. Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 6√2 = 6 * 2 = 12
Ответ: 12
F9EB9A
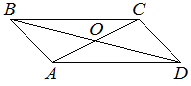
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 20/2 = 10
Ответ: 10
FF47FC

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=10, BD=22, AB=9. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 22/2 = 11
Ответ: 11
2E3469

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=14, BD=18, AB=5. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 18/2 = 9
Ответ: 9
99F180

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=16, BD=20, AB=5. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 20/2 = 10
Ответ: 10
8D3F15

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=22, BD=24, AB=3. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 24/2 = 12
Ответ: 12
F77141

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=20, BD=26, AB=8. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 26/2 = 13
Ответ: 13
F499CB

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=8, BD=14, AB=5. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 14/2 = 7
Ответ: 7
5CB1D4

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=6, BD=12, AB=4. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 12/2 = 6
Ответ: 6
111C58

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 28/2 = 14
Ответ: 14
F609D2

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=26, BD=30, AB=7. Найдите DO.
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 30/2 = 15
Ответ: 15
EF6511
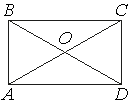
Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=7, AB=6. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 7 = 14
Ответ: 14
465856

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=8, AB=9. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 8 = 16
Ответ: 16
A9A357

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=11, AB=10. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 11 = 22
Ответ: 22
65D688

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=13, AB=11. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 13 = 26
Ответ: 26
6C9A50

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=15, AB=14. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 15 = 30
Ответ: 30
CA2EEA

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=17, AB=16. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 17 = 34
Ответ: 34
1DF080

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=23, AB=26. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 23 = 46
Ответ: 46
10AB30
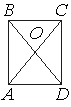
Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=12, AB=18. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 12 = 24
Ответ: 24
FDEE8C

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=37, AB=56. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 37 = 74
Ответ: 74
4E7064

Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=24, AB=45. Найдите AC.
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 24 = 48
Ответ: 48
7F3322

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac73$
значит, точка O делит отрезок AC в отношении 7:3, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 7+3=10 равных частей, 7 из которых составляет АО, а остальное – ОС, то есть:
АО = 20/10 * 7 = 14
Ответ: 14
2 способ
Рассмотрим треугольники AOD и BOC.
По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых.
Тогда: ∠DAO=∠BCO (накрест лежащие углы), ∠AOD=∠BOC (вертикальные углы).
Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Следовательно, можем записать пропорцию:
AD/BC=AO/OC
7/3=AO/OC
7*OC=3*AO
При этом
AO+OC=AC=20
OC=20-AO,
подставляем это равенство в ранее полученную пропорцию:
7*(20-AO)=3*AO
140-7*AO=3*AO
140=7*AO+3*AO
140=10*AO
AO=140/10=14
Ответ: 14
69759E

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac53$
значит, точка O делит отрезок AC в отношении 5:3, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 5+3=8 равных частей, 5 из которых составляет АО, а остальное – ОС, то есть:
АО = 24/8 * 5 = 15
Ответ: 15
4534C9

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=4, AD=9, AC=26. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac94$
значит, точка O делит отрезок AC в отношении 9:4, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 9+4=13 равных частей, 9 из которых составляет АО, а остальное – ОС, то есть:
АО = 26/13 * 9 = 18
Ответ: 18
A39540

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=2, AD=5, AC=28. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac52$
значит, точка O делит отрезок AC в отношении 5:2, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 5+2=7 равных частей, 5 из которых составляет АО, а остальное – ОС, то есть:
АО = 28/7 * 5 = 20
Ответ: 20
A2BB9D

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=7, AD=9, AC=32. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac97$
значит, точка O делит отрезок AC в отношении 9:7, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 9+7=16 равных частей, 9 из которых составляет АО, а остальное – ОС, то есть:
АО = 32/16 * 9 = 18
Ответ: 18
CB2FC8

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=5, AD=7, AC=36. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac75$
значит, точка O делит отрезок AC в отношении 7:5, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 7+5=12 равных частей, 7 из которых составляет АО, а остальное – ОС, то есть:
АО = 36/12 * 7 = 21
Ответ: 21
7A27E8

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=2, AD=8, AC=40. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac82$
значит, точка O делит отрезок AC в отношении 8:2, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 8+2=10 равных частей, 8 из которых составляет АО, а остальное – ОС, то есть:
АО = 40/10 * 8 = 32
Ответ: 32
7C7BEB

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=10, AD=14, AC=48. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac{14}{10}$
значит, точка O делит отрезок AC в отношении 14:10, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 14+10=24 равных части, 14 из которых составляет АО, а остальное – ОС, то есть:
АО = 48/24 * 14 = 28
Ответ: 28
4CF71D

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac{15}{11}$
значит, точка O делит отрезок AC в отношении 15:11, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 15+11=26 равных частей, 15 из которых составляет АО, а остальное – ОС, то есть:
АО = 52/26 * 15 = 30
Ответ: 30
30220A

Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38. Найдите AO.
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac{13}{6}$
значит, точка O делит отрезок AC в отношении 13:6, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 13+6=19 равных части, 13 из которых составляет АО, а остальное – ОС, то есть:
АО = 38/19 * 13 = 26
Ответ: 26
B4A79A
Задания с развернутым решением, 2-я часть ОГЭ
В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
22C756
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 1500, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
277E5E
В равнобедренную трапецию, периметр которой равен 80, а площадь равна 320, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
418268
В равнобедренную трапецию, периметр которой равен 220, а площадь равна 2420, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
B706A4
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
F311D0
В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
1EE527
В равнобедренную трапецию, периметр которой равен 100, а площадь равна 500, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
AA39FE
В равнобедренную трапецию, периметр которой равен 20, а площадь равна 20, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
9FFCAD
В равнобедренную трапецию, периметр которой равен 160, а площадь равна 1280, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
23E631
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение:
...
Ответ: ...
51A343

