Задания про середины сторон треугольника (в том числе про медиану, которая делит сторону пополам) из открытого банка ФИПИ к ОГЭ по математике, которые могут вам попасться на реальном экзамене в этом году.
Реальные задания по геометрии из банка ФИПИ
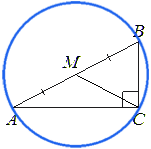
В треугольнике АВС угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 20/2 = 10
Ответ: 10
2 способ
Так как треугольник ABC прямоугольный, то воспользуемся теоремой об описанной окружности для прямоугольного треугольника.
Для этого опишем окружность вокруг треугольника ABC.
Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы.
Получается, что точка М и есть центр окружности, следовательно:
R = AM = MB = AB/2 = 20/2 = 10
CM тоже является радиусом окружности, т.е.:
CM = R = 10
Ответ: 10
EB170F

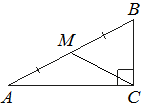
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=24, BC=14. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 24/2 = 12
Ответ: 12
A53D8B

В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=26, BC=18. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 26/2 = 13
Ответ: 13
0328E1

В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=32, BC=12. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 32/2 = 16
Ответ: 16
8D54E2

В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=36, BC=20. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 36/2 = 18
Ответ: 18
AD4D6B
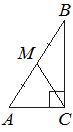
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=42, BC=30. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 42/2 = 21
Ответ: 21
EAA431

В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=48, BC=36. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 48/2 = 24
Ответ: 24
9CFFD3

В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 60/2 = 30
Ответ: 30
734E34

В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=64, BC=44. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 64/2 = 32
Ответ: 32
BB6457

В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=76, BC=46. Найдите CM.
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 76/2 = 38
Ответ: 38
483022
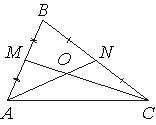
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
AO = 2
ON 1
Всего частей 3, следовательно,
AO = 2 ⇒
AN 3
AO = 2/3 * AN = 2/3 * 12 = 8
Ответ: 8
17EEFC
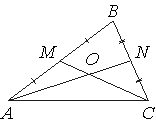
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
AO = 2
ON 1
Всего частей 3, следовательно,
AO = 2 ⇒
AN 3
AO = 2/3 * AN = 2/3 * 24 = 16
Ответ: 16
41A6C9

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
AO = 2
ON 1
Всего частей 3, следовательно,
AO = 2 ⇒
AN 3
AO = 2/3 * AN = 2/3 * 27 = 18
Ответ: 18
7C632F

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=27, CM=18. Найдите CO.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
СO = 2
OМ 1
Всего частей 2+1=3, следовательно,
СO = 2 ⇒
СМ 3
СO = 2/3 * СМ = 2/3 * 18 = 12
Ответ: 12
21CC51

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=12, CM=15. Найдите CO.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
СO = 2
OМ 1
Всего частей 2+1=3, следовательно,
СO = 2 ⇒
СМ 3
СO = 2/3 * СМ = 2/3 * 15 = 10
Ответ: 10
76623C

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=24, CM=9. Найдите CO.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
СO = 2
OМ 1
Всего частей 2+1=3, следовательно,
СO = 2 ⇒
СМ 3
СO = 2/3 * СМ = 2/3 * 9 = 6
Ответ: 6
EEDB1F

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=6, CM=9. Найдите ON.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
AO = 2
ON 1
Всего частей 3, следовательно,
ON = 1 ⇒
AN 3
ON = 1/3 * AN = 1/3 * 6 = 4
Ответ: 4
35398E

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=24, CM=18. Найдите ON.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
AO = 2
ON 1
Всего частей 3, следовательно,
ON = 1 ⇒
AN 3
ON = 1/3 * AN = 1/3 * 24 = 16
Ответ: 16
43E30F

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
AO = 2
ON 1
Всего частей 3, следовательно,
ON = 1 ⇒
AN 3
ON = 1/3 * AN = 1/3 * 33 = 22
Ответ: 22
B96811

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=12, CM=36. Найдите OM.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
СO = 2
OМ 1
Всего частей 2+1=3, следовательно,
ОМ = 1 ⇒
СМ 3
ОМ = 1/3 * СМ = 1/3 * 36 = 12
Ответ: 12
55480A

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
СO = 2
OМ 1
Всего частей 2+1=3, следовательно,
ОМ = 1 ⇒
СМ 3
ОМ = 1/3 * СМ = 1/3 * 15 = 5
Ответ: 5
55503E

Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
СO = 2
OМ 1
Всего частей 2+1=3, следовательно,
ОМ = 1 ⇒
СМ 3
ОМ = 1/3 * СМ = 1/3 * 21 = 7
Ответ: 7
D61C68
В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
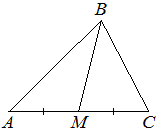
Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 14/2 = 7
Ответ: 7
67E364
В треугольнике ABC известно, что AC=16, BM — медиана, BM=12. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 16/2 = 8
Ответ: 8
E568B1
В треугольнике ABC известно, что AC=18, BM — медиана, BM=14. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 18/2 = 9
Ответ: 9
ABDD54
В треугольнике ABC известно, что AC=12, BM — медиана, BM=11. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 12/2 = 6
Ответ: 6
1893DC
В треугольнике ABC известно, что AC=36, BM — медиана, BM=13. Найдите AM.
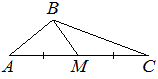
Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 36/2 = 18
Ответ: 18
D9FB5F
В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 38/2 = 19
Ответ: 19
41017F
В треугольнике ABC известно, что AC=32, BM — медиана, BM=23. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 32/2 = 16
Ответ: 16
77FDB2
В треугольнике ABC известно, что AC=34, BM — медиана, BM=26. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 34/2 = 17
Ответ: 17
060099
В треугольнике ABC известно, что AC=58, BM — медиана, BM=37. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 58/2 = 29
Ответ: 29
2889B5
В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 54/2 = 27
Ответ: 27
CF9F09
В треугольнике ABC известно, что AC=52, BM — медиана, BM=36. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 52/2 = 26
Ответ: 26
50022C
В треугольнике ABC известно, что AC=56, BM — медиана, BM=48. Найдите AM.

Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 56/2 = 28
Ответ: 28
60B4A9
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 21, сторона BC равна 22, сторона AC равна 28. Найдите MN.
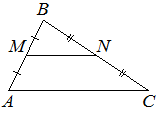
Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 28/2 = 14
Ответ: 14
1D9426
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 24, сторона BC равна 13, сторона AC равна 26. Найдите MN.
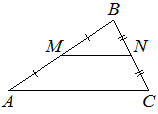
Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 26/2 = 13
Ответ: 13
BD7DDF
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 26, сторона BC равна 39, сторона AC равна 48. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 48/2 = 24
Ответ: 24
20402C
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 34/2 = 17
Ответ: 17
116AB8
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 42, сторона AC равна 50. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 50/2 = 25
Ответ: 25
E29AAA
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 42, сторона BC равна 44, сторона AC равна 62. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 62/2 = 31
Ответ: 31
C4C88B
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 27, сторона AC равна 40. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 40/2 = 20
Ответ: 20
6B712D
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 72/2 = 36
Ответ: 36
87FC25
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 83, сторона BC равна 62, сторона AC равна 104. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 104/2 = 52
Ответ: 52
D24F86
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 64/2 = 32
Ответ: 32
354F50
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 66, сторона BC равна 37, сторона AC равна 74. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 74/2 = 37
Ответ: 37
97C0BA
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 95, сторона BC равна 80, сторона AC равна 128. Найдите MN.

Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 128/2 = 64
Ответ: 64
8B61EB