§40. Расчет давления жидкости на дно и стенки сосуда

Вопросы

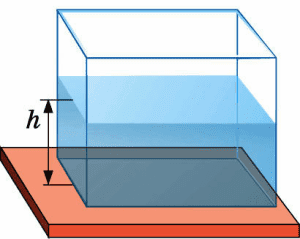
1. Выведите формулу для расчёта давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда.

Ответ:

Нам необходимо найти силу, условно F, с которой жидкость, что налита в сосуд, давит на его дно. Она равна весу P жидкости, находящейся в сосуде, то есть F=P. А вес жидкости можно определить, зная массу m (P = gm). Массу можно вычислить по формуле m = ρV.
Сам объём жидкости, налитой в параллелепипед, легко рассчитать. Для этого необходимо знать величины всех его сторон. V = Sh (S - площадь основания,  h - высота).
Масса жидкости m = ρV, или m = ρSh.
Вес этой жидкости P = gm, или P = gρSh.
А мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Тогда разделив вес P на площадь S, получим давление жидкости p:
$p=\frac{P}{S}$ или $p=\frac{gρSh}{S}$ или p = gρh

2. От каких величин и как зависит давление жидкости на дно сосуда?

Ответ:

P = gρh, где:
P − давление жидкости,
g = 9,8 Н/кг,
ρ − плотность жидкости,
h − высота столба жидкости.
Можно сделать заключение, что давление жидкости на дно сосуда зависит от плотности и высоты столба жидкости. 

3. По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?

Ответ:

Также как и итоговое значение давление, так и давление на стенки на определенной глубине будет рассчитываться по той же самой формуле. Разве что значение глубины будет другим. p = gρh (где − p − давление жидкости, g = 9,8 Н/кг, ρ − плотность жидкости, h − высота столба жидкости), так как давление на одной и той же глубине одинаково по всем направлениям.

Упражнение 17

1. Определите давление на глубине 0,6 м в воде, керосине, ртути.

Ответ:

Дано:
h = 0,6 м;
$ρ_{в}$ = 1000 кг/$м^{3}$;
$ρ_{к}$ = 800 кг/$м^{3}$;
$ρ_{рт}$ = 13600 кг/$м^{3}$;
$p_{в}$−?
$p_{к}$ − ?
$p_{рт}$−?
Решение:
$p = gρh$;
g ≈9,8 Н/кг;
$p_{в}$ = 9,8 * 1000 * 0,6 = 5880 Па;
$p_{к}$ = 9,8 * 800 * 0,6 = 4704 Па;
$p_{рт}$ = 9,8 * 13600 * 0,6 = 79968 Па ≈ 80 кПа
Ответ. 5880 Па, 4704 Па, 80 кПа.

2. Вычислите давление воды на дно одной из глубочайших морских впадин — Марианской, глубина которой 10 900 м. Плотность морской воды 1030 $кг/м^{3}$.

Ответ:

Дано:
h = 10 900 м;
ρ = 1030 кг/$м^{3}$.
p−?
Решение:
p = gρh;
g = 9,8 Н/кг;
p = 9,8 * 1030 * 10900 = 110024600 Па ≈ 110 МПа
Ответ. 110 МПа

3. На рисунке 113 изображена футбольная камера, соединённая с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на неё — гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.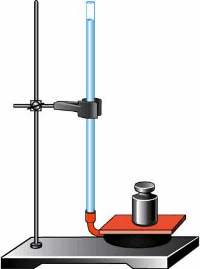

рис. 113

Ответ:

Дано:
m = 5 кг;
h = 1 м;
$ρ_{в} = 1000 кг/м^{3}$;
S−?
Решение:
$p_{1}=\frac{F}{S}$ − давление гири на доску;
$p_{2}= gρh$ − давление столба воды в трубке.
Делаем заключение, если дощечка находится в равновесии, то давление на неё гири должно ровняться давлению водяного столба.
$p_{1}=p_{2}$;
F=gm;
$\frac{gm}{S} =gρh$;
$S=\frac{gm}{gρh} = \frac{m}{ρh}$;
$S=\frac{5}{1000 * 1}$ = 0,05 $м^{3}$.
Ответ. 0,05 $м^{3}$.

Задание

1. Возьмите высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и наполните сосуд водой. Откройте отверстия и проследите за струйками вытекающей воды (рис. 114). Почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной?

рис. 114

Ответ:

 Жидкость имеет свой вес и притягивается к земле. При этом при увеличении высоты столба жидкости, верхние слои с большим усилием давят на нижние. В итоге мы можем наблюдать, что через более низкие по уровню отверстия, жидкость вытекает с под большим давлением, струя сильнее, бьет дальше.

2. Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте давление воды на дно сосуда.

Ответ:

Дано:
h = 0,15 м;
$ρ_{в}$ = 1000 кг/$м^{3}$;
p−?
Решение:
p = gρh;
g ≈ 9,8 Н/кг;
p = 9,8 * 1000 * 0,6 = 1470 Па;
Ответ. 1470 Па.