Ответы к странице 75

65. Вадим купил для себя 18 одинаковых тетрадей, а для соседа – 12 таких же тетрадей. За всю покупку он за платил 450 р. Сосед принёс ему купюру в 500 р. Сколько сдачи Вадим должен ему вернуть?

Решение:

1) 18 + 12 = 30 (т.) - купил Вадим
2) 450 : 30 = 15 (р.) - стоит тетрадь
3) 12 *30 = 360 (р.) - Вадим отдал за тетради соседа
4) 500 - 360 = 140 (р.) - должен отдать сдачи
Ответ: 140 рублей.

66. Первый маляр за 3 ч покрасил потолок в комнате площадью 27 м2. Второй маляр, выполняя такую же работу, потратил на 2 ч больше времени. Но площадь его комнаты была на 13 м2 больше, чем у первого. У кого из них производительность больше и на сколько?

Решение:

1) 27 : 3 = 9 (м²/ч) - производительность первого маляра.
2) 3 + 2 = 5 (ч) - потратил второй маляр. 
3) 27 + 13 = 40 (м²) - покрасил второй маляр.
4) 40 : 5 = 8 (м²/ч) - производительность второго маляра.
5) 9 - 8 = 1 (м²/ч) - на столько производительность первого маляра выше, чем второго.
Ответ: на 1 м²/ч.

67. Саше надо отметить точку М, нарисовать луч АК, отрезок ВС и прямую EF. На рисунке показан его чертёж. Какие ошибки он допустил? Нарисуй в тетради указанные фигуры правильно.

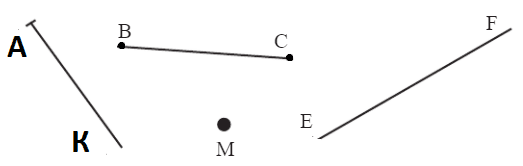
68. Построй:

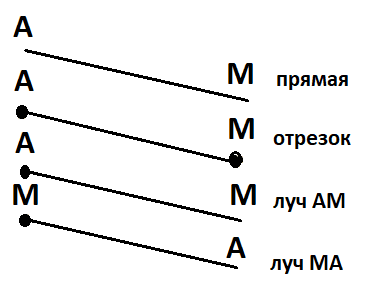
а) прямую АМ;
б) отрезок АМ;
в) луч АМ;
г) луч МА.

Решение:

69.

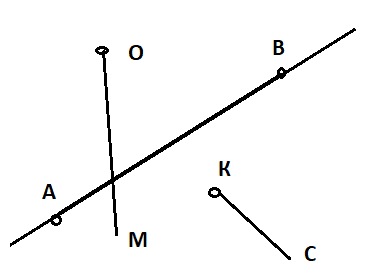
а) Отметь две точки А и В, проведи через них прямую. Начерти луч ОМ, пересекающий прямую АВ, и луч КС, её не пересекающий.

Решение:

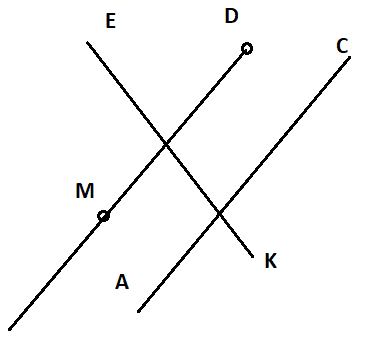
б) Отметь точки М и D и проведи луч DM. Начерти прямую EK, которая пересекает луч DM, и прямую АС, которая его не пересекает.

Решение:

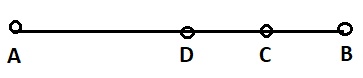
70. Построй отрезок AB = 5 см 4 мм и отметь на нём точки C и D так, чтобы точка C лежала между точками B и D. Измерь отрезок BC.

Решение:

Строим отрезок, отмечаем точки. Получившиеся измерения могут быть самыми разными, поэтому измеряем конкретно для вашего случая.

71. Измерь с помощью линейки стороны многоугольника и найди его периметр. Сколько у него острых углов, прямых, тупых?

Решение:

По нашим измерениям 18 см. 
АВ = 4 см
ВС = 5 см
СD = 3 см
DE = 4 см
EA = 2 см

72. Найди в окружающей обстановке предметы, которые могут служить моделями отрезков. Рассмотри с помощью этих моделей возможные случаи взаимного расположения двух отрезков. Опиши их словами и изобрази на чертеже.

Решение

Стороны листа бумаги:

Решение:

Плинтуса по полу:

Жерди (перемычки) в заборе: