Ответы к странице 136

Задание 742

Восстановите цепочки вычислений и попробуйте объяснить, почему они приводят к одному ответу: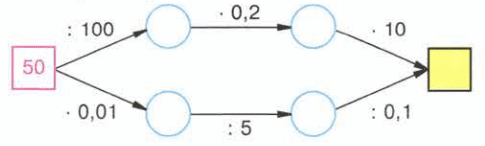

Решение

50 → 0,5 → 0,1 → 1
50 → 0,5 → 0,1 → 1
Деление производится на обратное умножению число.

Задание 743

Собственная скорость катера 18 км/ч. Отметьте её на координатном луче. Вычислите и отметьте на этом луче скорости катера против течения и по течению, если скорость течения 1,5 км/ч. Используя чертёж, подумайте:
а) как найти собственную скорость катера, если известны его скорости по течению и против течения;
б) как найти скорость катера против течения, если известны скорость течения и скорость катера по течению;
в) на сколько скорость катера по течению больше его скорости против течения?

Решение

а) При известных скоростях катера по течению и против собственная скорость катера равна среднему арифметическому этих скоростей.

б) При известной скорости катера по течению и скорости течения скорость против течения равна разности скорости по течению и удвоенной скорости течения.

в) Скорость катера по течению больше скорости против течения на величину удвоенной скорости течения.

Задание 744

Попробуйте представить правило нахождения среднего арифметического нескольких чисел и средней скорости в виде последовательности команд по схемам:...

Решение

Чтобы найти среднее арифметическое нескольких чисел, нужно:
1) найти сумму этих чисел;
2) найти число этих чисел;
3) разделить сумму чисел на их число.
Чтобы найти среднюю скорость, нужно:
1) найти пройденный путь;
2) найти общее время движения;
3) разделить пройденный путь на время движения.

Задание 745

Найдите значение выражения:
а) 2,0928 + 47,9072 : (7 − 0,195);
б) 100,5876 − 88,5856 : (6,0811 + 8,4889);
в) 687,8 + (88,0802 − 85,3712) : 0,045.
Проверьте ответ с помощью микрокалькулятора.

Решение

а) 2,0928 + 47,9072 : (7 − 0,195) = 2,0928 + 47,9072 : 6,805 = 2,0928 + 7,04 = 9,1328

б) 100,5876 − 88,5856 : (6,0811 + 8,4889) = 100,5876 − 88,5856 : 14,57 = 100,5867 − 6,08 = 94,5076

в) 687,8 + (88,0802 − 85,3712) : 0,045 = 687,8 + 2,709 : 0,045 = 687,8 + 60,2 = 748

Задание 746

Автобус шёл 3 ч по шоссе, 1,5 ч по грунтовой дороге и 0,5 ч по просёлочной дороге. Известно, что скорость автобуса по грунтовой дороге была в 2 раза больше скорости по просёлочной дороге, а скорость по шоссе в 3,5 раза больше скорости по просёлочной дороге. Найдите скорость движения автобуса по просёлочной дороге, если средняя скорость автобуса на всём пути 33,6 км/ч.

Решение

Пусть скорость автобуса по проселочной дороге − х км/ч ,
тогда его скорость по грунтовой дороге − 2х км/ч,
а скорость автобуса по шоссе − 3,5х км/ч.
Средняя скорость автобуса на всем маршруте равна:
(3,5х − 3 + 2x1,5 + х − 0,5) : (3 + 1,5 + 0,5) км/ч.
Составим уравнение:
(3,5х − 3 + 2x1,5 + х − 0,5) : (3 + 1,5 + 0,5) = 33,6
10,5х + 3х + 0,5х = 33,6 − 5 
14х = 168
х = 168 : 14
х = 12
Значит, скорость движения автобуса по просёлочной дороге 12 км/ч.
Ответ: 12 км/ч.