Ответы к странице 152
Задание 829
Найдите пропущенные числа:
Решение
а) Число: 0,8/3,6.
Правило: числитель каждой следующей дроби на 0,1 меньше числителя предыдущей дроби, а знаменатель каждой следующей дроби на 0,8 больше знаменателя предыдущей дроби.
б) Число: 0,05/0,15.
Правило: числитель и знаменатель каждой дроби через одну в 4 раза меньше числителя и знаменателя предыдущей дроби через одну.
Задание 830
Стреляя в тире, Дима в 76% случаев попал в мишень. Сколько промахов допустил Дима, если всего он произвёл 50 выстрелов?
Решение
1) 100% − 76% = 24% случаев Дима не попал в мишень
2) 50 : 100 * 24 = 12 (п.) - совершил Дима
Ответ: 12 промахов.
Задание 831
За три дня в магазине продано 1280 кг яблок. В первый день продали 25% всех яблок, а во второй день − 45% всех яблок. Сколько килограммов яблок продали в третий день? Решите задачу двумя способами. Какой из этих способов проще?
Решение
1 способ.
25% = 0,25
1) 1280 * 0,25 = 320 (кг) - яблок продано в первый день
45% = 0,45
2) 1280 * 0,45 = 576 (кг) - яблок продано во второй день
3) 1280 − (320 + 576) = 1280 − 896 = 384 (кг) - яблок продано в третий день
Ответ: 384 кг.
2 способ.
1) 100% − (25% + 45%) = 100% − 70% = 30% всех яблок продано в третий день
2) 1280 : 100 * 30 = 384 (кг) - яблок продано в третий день
Ответ: 384 кг.
Второй способ решения проще первого.
Задание 832
Объясните смысл предложения:
а) «Из молока получается 25% сливок»;
б) «В свёкле содержится 20% сахара».
Решение
а) Это означает, что из х л молока получается 0,25x л сливок.
б) Это означает, что из х кг свёклы получается 0,2х кг сахара.
Задание 833
При перегонке нефти получается 30% керосина. Сколько керосина можно получить из 12 т; из 28 т; из 36,5 т нефти?
Решение
30% = 0,3
1) 12 * 0,3 = 3,6 (т) - керосина получается из 12 т нефти
2) 28 * 0,3 = 8,4 (т) - керосина получается из 28 т нефти
3) 36,5 * 0,3 = 10,95 (т) - керосина получается из 36,5 т нефти
Ответ: 3,6 т, 8,4 т, 10,95 т.
Задание 834
Решите задачу:
1) Площадь поля 560 га. В первый день засеяли 3/7 поля, а остальное − во второй день.
Сколько гектаров засеяли во второй день?
2) Площадь поля 450 га. Овсом засеяли 2/5 поля, а пшеницей − остальную часть.
Сколько гектаров засеяли пшеницей?
Решение
1) 1 − 3/7 = 4/7 всего поля засеяли во второй день,
560 * 4/7 = 80 * 4 = 320 (га) - асеяли во второй день
Ответ: 320 га.
2) 1 − 2/5 = 3/5 поля засеяли пшеницей
450 * 3/5 = 90 * 3 = 270 (га) - засеяли пшеницей
Ответ: 270 га.
Задание 835
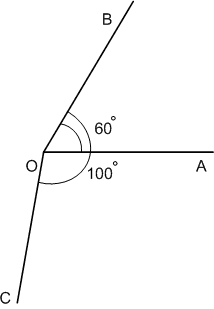
Начертите два угла − в 60° и в 100° − с общей вершиной так, чтобы они имели общую сторону и лежали по разные стороны от неё. Найдите градусную меру угла, образованного двумя другими сторонами этих углов.
Решение
∠AOB = 60°, ∠AOC = 100°, ∠BOC = 100° + 60° = 160°.
Задание 836
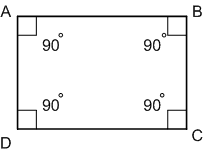
Начертите произвольный четырёхугольник ABCD, измерьте транспортиром его углы и сложите результаты измерений.
Решение
∠DAB = 90°, ∠CDA = 90°, ∠ABC = 90°, ∠BCD = 90°;
∠DAB + ∠CDA + ∠ABC + ∠BCD = 90° + 90° + 90° + 90° = 360°.
Задание 837
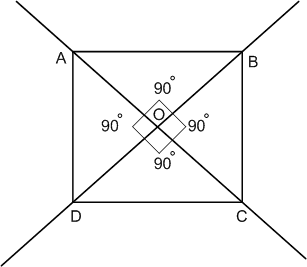
Начертите произвольный четырёхугольник ABCD и проведите прямые АС и BD. Измерьте транспортиром углы АОВ, ВОС, COD и DOA, где О − точка пересечения прямых АС и BD. Какие из этих углов имеют одинаковую градусную меру? Сумма градусных мер каких углов равна 180°?
Решение
∠COD = 90°,
∠BOC = 90°,
∠AOB = 90°,
∠AOD = 90°,
∠AOB = ∠COD, ∠BOC = ∠AOD;
∠AOB + ∠BOC = ∠BOC + ∠COD = ∠COD + ∠DOA = ∠AOD + ∠AOB = 180°.
Задание 838
Найдите градусные меры углов треугольника MNKy если угол М меньше угла N на 40° и больше угла К на 10°.
Решение
Пусть градусная мера ∠M равна х, тогда ∠N = (х + 40)°, а ∠К = (х − 10)°.
Составим уравнение:
x + x + 40 + x − 10 = 180
3x + 30 = 180
х = (180 − 30) : 3
х = 50°.
∠M = 50°, ∠N = 50 + 40 = 90°, ∠K = 50 − 10 = 40°.
Задание 839
Найдите градусные меры углов треугольника CDE, если угол С вдвое больше угла D и втрое меньше угла Е.
Решение
Пусть ∠D = х°, тогда ∠C = 2х°, a ∠E = 3 * 2х°.
Составим уравнение:
х + 2х + 3 * 2х = 180
х = 180 : 9
х = 20°.
∠D = 20°, ∠C = 2 * 20 = 40°, ∠E = 3 * 40 = 120°.