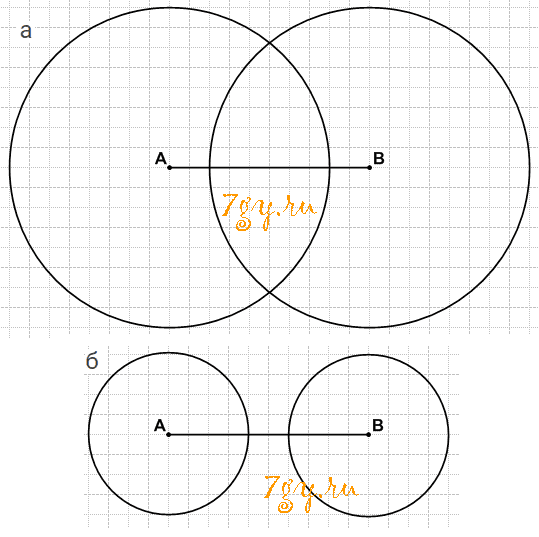Ответы к странице 19
Задание 68
Сколько в действительности времени, если часы, отражённые в зеркале (рис. 21), показывают 9 ч; 8 ч; 6 ч 15 мин; 10 ч 40 мин? Когда часы и их отражение покажут одинаковое время?
Решение
Показания часов в зеркале и их показания в действительности симметричны относительно вертикальной оси, проходящей через цифры 6 и 12. Поэтому 9 ч в зеркале − это 3 ч в действительности, 8 ч − 4 ч, 6 ч 15 мин − это 5 ч 45 мин, 10 ч 40 мин − это 1 ч 20 мин. Одинаковое время на часах будет, когда минутная и часовая стрелки находятся одновременно на вертикальной оси, то есть в 12 ч и 6 ч.
Задание 69
Отметьте точки А и В так, что АВ = 5 см. Проведите окружности одинакового радиуса с центрами А и B так, чтобы они:
а) пересекались в двух точках;
б) не имели общих точек.
Задание 70
Начертите отрезок АВ = 6 см. Найдите точки, которые удалены от А и от В на 6 см.
Решение
Точки C и D удалены от А и от В на 6 см.
Задание 71
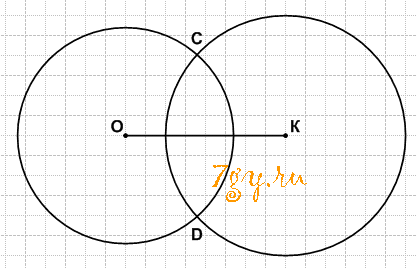
Начертите окружность с центром в точке О и радиусом 2 см 6 мм (рис. 22). Отметьте такую точку К, чтобы ОК = 4 см. Найдите с помощью циркуля на окружности точки, удалённые от точки К на 3 см.
Решение
Точки С и D удалены от точки K на 3 см.
Задание 72
Бетонный блок имеет длину 12 дм, ширину 8 дм и высоту 5 дм. Из таких блоков сложили стену длиной 240 дм, шириной 24 дм и высотой 30 дм. Сколько блоков потребовалось для этого?
Решение
1) 12 * 8 * 5 = 480 (дм3) - объем одного блока.
2) 240 * 24 − 30 = 172800 (дм3) - объем стены.
3) 172 800 : 480 = 360 (б.) - потребовалось
Ответ: на строительство стены потребовалось 360 блоков.
Задание 73
На книжную полку ставят 6 разных книг. Сколькими способами эти книги можно разместить на полке?
Решение
6! = 1 * 2 * 3 * 4 * 5 * 6 = 720 (с.)
Ответ: 720 способами.
Задание 74
Решите задачу:
1) В двух спортивных секциях поровну участников. Если в каждую из них войдут ещё по 2 участника, то всего в них будет 36 человек. Сколько человек занимается в каждой секции?
2) В трёх классах поровну учащихся. Если в каждый класс добавить ещё по 3 учащихся, то всего в них будет 129 учащихся. Сколько человек учится в каждом классе?
Решение
1) Пусть в каждой секции занимается х человек, тогда после пополнения всего будут
заниматься 2 * (х + 2) человека.
Составим и решим уравнение:
2(х + 2) = 36
х + 2 = 36 : 2 = 18
х = 18 − 2
х = 16 (ч.)
Ответ: по 16 человек занимается в каждой секции.
2) Пусть в каждом классе х учащихся, тогда в каждом классе станет (x + 3) учащихся.
Общее число учащихся будет 3 * (х + 3) человека.
Составим и решим уравнение:
3 * (х + 3) = 129
у + 3 = 129 : 3 = 43
у = 43 − 3
у = 40 (уч.)
Ответ: по 40 учащихся в каждом классе.
!Задание 75
Выполните действия:
1) 90 720 : (207 : 23 * 840);
2) 22 624 : 56 * (816 : 8);
3) 14 700 : 21 : 7 * 49;
4) 140 : 10 : (49 : 7) : (10 : 5).
Решение
1) 90720 : (207 : 23 * 840) = 90720 : (9 * 840) = 90720 : 7560 = 12
2) 22624 : 56 * (816 : 8) = 404 * 102 = 41208
3) 14700 : 21 : 7 − 49 = 700 : 7 − 49 = 100 * 49 = 4900
4) 140 : 10 : (49 : 7) : (10 : 5) = 14 : 7 : 2 = 2 : 2 = 1