Ответы к странице 188
Задание 1058
Упростите выражение:
а) 5а + 12,4 + 2,6 + 3,14 + 1,4а + 0,4а + 2,4;
б) 13,4 + 6 + 5,6 + 8,2b + 7,28 + 1,7b + 2,3.
Решение
а) 5a + 12,4 + 2,6 + 3,14 + 1,4a + 0,4a + 2,4 = 6,8a + 20,54
б) 13,4 + 6 + 5,6 + 8,2b + 7,28 + 1,7b + 2,3 = 9,9b + 34,58
Задание 1059
Найдите значение выражения:
а) 19,1у + 121,4 + 0,9у при у = 48,5;
б) 5,6m + 8,4m + 186,4 при m = 35,5.
Решение
а) 19,1y + 121,4 + 0,9y = 20y + 121,4
при y = 48,5 => 20 * 48,5 + 121,4 = 970 + 121,4 = 1091,4
б) 5,6m + 8,4m + 186,4 = 14m + 186,4
при m = 35,5 => 14 * 35,5 + 186,4 = 497 + 186,4 = 683,4
Задание 1060
В пяти маленьких и двух больших коробках 54 цветных карандаша, а в трёх маленьких и двух больших коробках 42 карандаша. Сколько карандашей в одной маленькой и сколько в одной большой коробке?
Решение
Из условий задачи следует, что 2 маленькие коробки содержат
1) 54 − 42 = 12 (к.) - содержат 2 маленькие коробки
2) 12 : 2 = 6 (к.) - содержит 1 маленькая коробка
3) (42 − 6 * 3) : 2 = (42 − 18) : 2 = 12 (к.) - содержит одна большая коробка
Ответ: 6 и 12 карандашей.
Задание 1061
Длина прямоугольника в 5 раз больше его ширины. Найдите стороны прямоугольника, если его периметр 1212 см.
Решение
Пусть х − ширина прямоугольника,
тогда 5х − его длина.
Составим уравнение:
2 * (х + 5х) = 1212
6х = 1212 : 2 = 606
х = 606 : 6
х = 101
Значит, ширина прямоугольника 101 см,
5 * 101 = 505 (см) - длина прямоугольника
Ответ: 101 см, 505 см.
Задание 1062
В одной бочке было в 3 раза больше бензина, чем в другой. Когда в первую налили ещё 46 л, а во вторую 18 л, то в двух бочках стало 184 л бензина. Сколько литров бензина было в каждой бочке первоначально?
Решение
Пусть х − количество бензина в первой бочке,
тогда 3х − количество бензина во второй бочке.
Составим уравнение:
(3x + 46) + (х + 18) = 184
4х = 184 − 46 − 18 = 120
х = 120 : 4
х = 30
Значит, объем первой бочки 30 л,
3 * 30 = 90 (л) − объем второй бочки.
Ответ: 30 л, 90 л.
Задание 1063
Площадь земли, засеянной пшеницей, в 6 раз больше площади, засеянной ячменём, а площадь, засеянная рожью, в 3 раза меньше площади, засеянной пшеницей. Сколько гектаров земли засеяно каждой культурой, если рожью засеяно на 120 га больше, чем ячменём?
Решение
Пусть засеяно ячменем − х,
тогда засеяно пшеницей − 6x,
а засеяно рожью − 6х : 3 = 2х.
Составим уравнение:
2х − х = 120
х = 120
Значит, 120 га засеяно ячменём,
2 * 120 = 240 (га) − засеяно рожью,
6 * 120 = 720 (га) − засеяно пшеницей.
Ответ: 120 га, 240 га, 720 га.
Задание 1064
В зрительном зале кинотеатра 16 рядов, и в каждом ряду 24 места. Сколько денег выручит кинотеатр за 3 сеанса, если цена билета m р. и на эти сеансы все билеты будут проданы?
Решение
3 * 16 * 24 * m
Задание 1065
Измерьте углы АОВ, ВОС, DMN, NME (рис. 113). Какие из этих углов равны?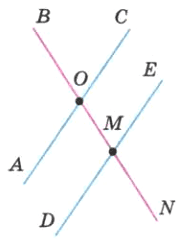
Решение
∠AOB = ∠NME
∠BOC = ∠DMN
Задание 1066
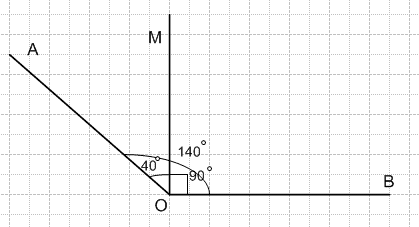
Постройте угол АОВ в 140° и проведите луч ОМ так, чтобы он разделил угол АОВ на два угла, один из которых на 40° больше другого.
Решение
∠AOM − ∠MOB = 40°
∠AOM + ∠MOB = 140°
∠MOB = (140° − 40°) : 2 = 50°
∠AOM = 50°+ 40° = 90°
Задание 1067
Найдите объём прямоугольного параллелепипеда, если его длина 2,3 см, ширина 1,4 см, а высота 0,5 см.
Решение
V = a b c = 2,3 * 1,4 * 0,5 = 1,61 (см³) - объём прямоугольного параллелепипеда
Ответ: 1,61 см³.
Задание 1068
Длина прямоугольного параллелепипеда равна а см, ширина − на 2 см меньше длины, а высота равна 5 см. Составьте выражение для нахождения объёма этого параллелепипеда.
Решение
V = abc = a(a − 2) * 50 = 50a * (a − 2).
Задание 1069
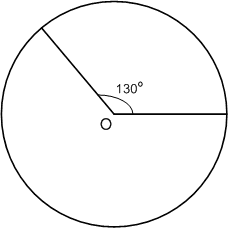
Начертите окружность и постройте два радиуса этой окружности так, чтобы угол между ними был равен 130°.
Решение
Задание 1070
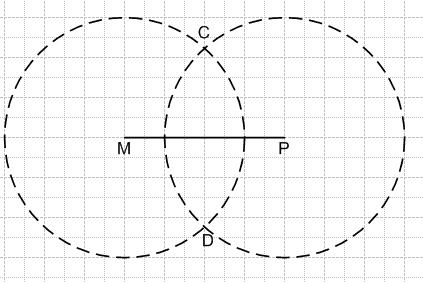
Начертите отрезок МР, длина которого 4 см, и найдите две точки, удалённые от концов отрезка на 3 см.
Решение