Ответы к странице 181

Задание 992

На отрезке MN отмечены две точки С и D так, что точка С лежит между точками N и D. Найдите длину отрезка MNy если DC = 2 см, DN = 6 см, МС = 5 см.

Решение

MN = MD + DC + CN = (MC − DC) + DC + DN − DC = MC + DN − DC = 6 + 5 − 2 = 9 см.

Задание 993

Стороны многоугольника ABCDE равны: АВ = 6,4 см, ВС = 5 см, CD = 6,3 см, DE = 5,8 см и АЕ = 3 см. Найдите периметр этого многоугольника. Как называется такой многоугольник? Что такое периметр многоугольника?

Решение

PABCDE = AB + BC + CD + DE + AE = 6,4 + 5 + 6,3 + 5,8 + 3 = 26,5 см.
ABCDE − пятиугольник.

Задание 994

С помощью какого инструмента можно найти:
а) длину отрезка;
б) градусную меру угла?
В каких единицах измеряются эти величины?

Решение

а) с помощью линейки

б) с помощью транспортира

Длина измеряется в миллиметрах, сантиметрах, дециметрах, метрах и километрах.
Углы измеряется в градусах.

Задание 995

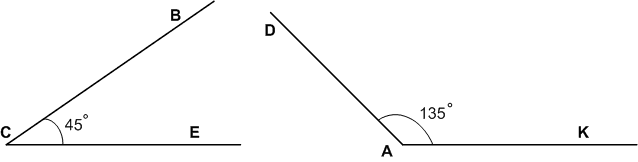
Начертите острый угол ВСЕ и тупой угол DAK и определите их градусные меры. Начертите прямой угол Р и развёрнутый угол М. Какова градусная мера прямого угла? развёрнутого угла? Какую часть развёрнутого угла составляет угол в 1°?

Решение

∠ВСЕ = 45° < 90° − острый угол, 90° < ∠DAK = 135° < 180° − тупой угол,
∠P = 90° − прямой угол, ∠M = 180° − развернутый угол.
Угол в 1° составляет 1/180 часть развернутого угла.

Задание 996

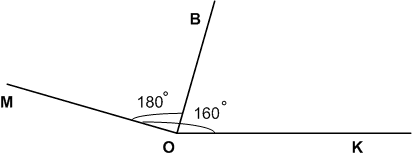
Начертите угол МОК в 160°. Проведите луч ОВ так, чтобы он разделил угол МОК пополам. Как называется такой луч?

Решение

Луч ОB называется биссектрисой угла МОК.

Задание 997

Начертите четырёхугольник ABCD, у которого ∠A = 40°, ∠B = 140°, ∠C = 50°. Измерьте величину угла D.

Решение

Величина угла ∠D = 130°.

Задание 998

Угол АОВ на рисунке 103 разделён на 5 равных углов. Назовите углы, которые составляют 3/5 угла АОВ. Найдите величину угла СОР, если угол АОВ равен 100°.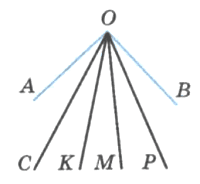

Решение

∠ AOM =∠ COP =∠ KOB = 3/5 ∠ AOB;
∠ COP = 100 * 3/5 = 60 °.

Задание 999

На рисунке 104 угол АОС равен углу DOB. Докажите, что угол АО В равен углу COD.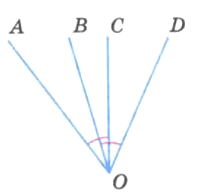

Решение

∠AOB + ∠DOB = ∠AOD;
∠COD + ∠AOC = ∠AOD;
∠AOB = ∠AOD − ∠DOB;
∠COD = ∠AOD − ∠AOC.
Так как ∠DOB = ∠AOC => ∠AOB = ∠COD.

Задание 1000

Прямые АВ и CD (рис. 105) пересекаются в точке О. Докажите, что углы АОС и BOD равны.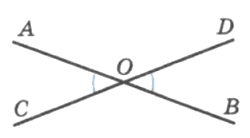

Решение

∠AOB = ∠COD = 180°;
∠COD = ∠AOC + ∠AOD;
∠AOB = ∠AOD + ∠BOD;
∠AOD + ∠AOC = ∠AOD+ ∠BOD;
∠AOC = ∠BOD + ∠AOD − ∠AOD;
∠AOC = ∠BOD.

Задание 1001

Не пользуясь транспортиром, определите угол между стрелками часов на рисунке 106.

Решение

а) 30° * 2 = 60°

б) 5 * 30° = 150°

в) 1,5 * 30° = 45°

г) 3,5 * 3° = 10,5°

д) 4,5 * 30° = 135°