Ответы к странице 30
Задание № 141
Какая часть четырёхугольника ABCD (рис. 33) закрашена? Какая часть осталась незакрашенной?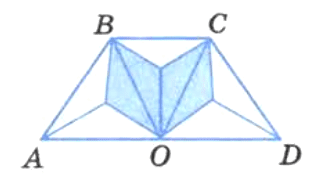
Решение
Закрашено 4/9 четырехугольника ABCD, осталось не закрашено 5/9 четырехугольника.
Задание № 142
Выразите в граммах:
а) 3 кг 400 г;
б) 2 кг 30 г;
в) 15 кг.
Решение
a) 3 кг 400 г = 3400 г
б) 2 кг 30 г = 2030 г
в) 15 кг = 15000 г
Задание № 143
Расположите в порядке возрастания дроби:4/11;2/11;10/11;9/11;8/11;7/11.
Расположите эти же дроби в порядке убывания.
Решение
В порядке возрастания: $\frac2{11}<\frac4{11}<\frac7{11}<\frac8{11}<\frac9{11}<\frac{10}{11}$
В порядке убывания: $1\frac{10}{11}>\frac9{11}>\frac8{11}>\frac7{11}>\frac4{11}>\frac2{11}$
Задание № 144
Назовите четыре дроби, которые меньше, чем 1/1000000.
Решение
$\frac1{1100000}<\frac1{1010000}<\frac1{1001000}<\frac1{1000100}<\frac1{1000000}$
Задание № 145
Назовите 5 дробей, которые больше, чем 1/9.
Решение
$\frac69>\frac59>\frac49>\frac39>\frac29>\frac19$
Задание № 146
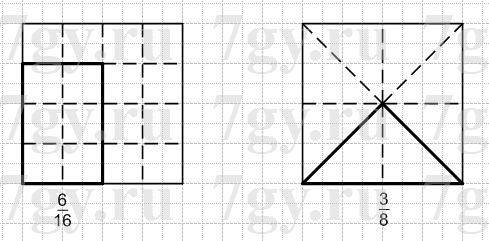
Начертите квадрат со стороной 4 см. Покажите на чертеже: 6/16 квадрата, 3/8 квадрата. Найдите площади этих частей квадрата и объясните полученный результат.
Решение
$S_{квадрата}=4\ast4=16\;(см^2)$
$16\ast6:16=6\;(см^2)$ - площадь 6/16 квадрата;
$16\ast3:8=6\;(см^2)$ - площадь 3/8 квадрата.
Задание № 147
В первый день бригада собрала 5 т 400 кг картофеля, а во второй − на 1 т 200 кг меньше, чем в первый. В третий день бригада собрала в 2 раза больше картофеля, чем во второй. Сколько картофеля собрано бригадой за эти три дня?
Решение
1) 5 т 400 кг − 1 т 200 кг = 5400 кг − 1200 кг = 4200 кг картофеля собрала бригада во второй день
2) 2 * 4200 = 8400 (кг) - картофеля собрала бригада в третий день
3) 5400 + 4200 + 8400 = 18000 (кг) = 18 (т) - картофеля собрала бригади за 3 дня
Ответ: 18 т картофеля.
Задание № 148
Составьте задачу по уравнению:
а) (у + 6) − 2 = 15;
б) 2(a − 5) = 24;
в) 3(25 + b) + 15 = 135.
Решение
а) У Вити было на 6 рублей больше чем у Пети. Сколько рублей было у Пети, если у Вити, истратившего 2 рубля осталось 15 рублей.
Пусть у Пети было y рублей, тогда у Пети было у + 6 рублей.
Составим уравнение:
(у + 6) − 2 = 15
у + 4 = 15
y = 15 − 4 = 11 (р.) - было у Пети
б) Скорость первого велосипедиста на 5 км/ч меньше скорости второго велосипедиста. Найдите скорость второго велосипедиста, если первый велосипедист за 2 часа проехал 24 км.
Пусть скорость второго велосипедиста равна а км/ч, тогда скорость первого велосипедиста равна (а − 5) км/ч.
Составим уравнение:
2(a − 5) = 24
2a − 10 = 24
2a = 24 + 10 = 34
a = 34 : 2 = 17 (км/ч) - скорость второго велосипедиста
в) Расстояние между селом и городом равно 135 км. Найдите скорость мотоцикла, если известно, что автомобиль, выехавший из села со скоростью на 25 км/ч больше скорости мотоцикла, через три часа не доехал до города 15 км.
Пусть скорость мотоцикла равна b км/ч, тогда скорость автомобиля равна (25 + b) км/ч.
Составим уравнение:
3(25 + b) + 15 = 135
75 + b + 15 = 135
b = 135 − 75 − 15 = 45 (км/ч) - скорость мотоцикла
Задание № 149
В первом вагоне ехали а человек, а во втором − b человек. На остановке из первого вагона вышли с человек, а из второго − d человек. Какой смысл имеют следующие выражения:
a + b; с + d; (a + b) − (с + d);
a − с; b − d; (a − с) + (b − d)?
Объясните, почему
(a + b) − (c + d) = (a − c) + (b − d) при а > с, b > d.
Проверьте это равенство при а = 45, b = 39, с = 14, d = 12.
Используя полученное равенство, вычислите значение выражения:
а) (548 + 897) − (148 + 227);
б) (391 + 199) − (181 + 79).
Решение
a + b − количество пассажиров в первом и втором вагонах,
с + d − общее количество вышедших пассажиров,
(a + b) − (с + d) − количество оставшихся пассажиров в первом и втором вагонах,
a − с − количество пассажиров, оставшихся в первом вагоне,
b − d − количество пассажиров, оставшихся во втором вагоне;
(a − с) + (b − d) = a − c + b − d = (a + b) − (с + d).
Если a = 45, b = 39, с = 14, d = 12,
(a + b) − (с + d) = (45 + 39) − (14 + 12) = 84 − 26 = 58;
(a − c) + (b − d) = (45 − 14) + (39 − 12) = 31 + 27 = 58.
а) (548 + 897) − (148 + 227) = (548 − 148) + (897 − 227) = 400 + 670 = 1070
б) (391 + 199) − (181 + + 79) = (391 − 181) + (199 − 79) = 210 + 120 = 330