Ответы к странице 150
Задание 815
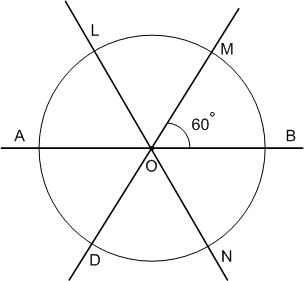
Начертите круг радиусом 3 см. Обозначьте его центр буквой О. Проведите через точку О прямую АВ. С помощью транспортира разделите развёрнутые углы AОВ с обеих сторон прямой на 3 равных угла. На сколько равных частей разделился круг?
Решение
Круг разделен на 6 равных частей.
Задание 816
Угол АОВ развёрнутый, а ОС − луч. Найдите градусные меры углов АОС и СОВ, если:
а) градусная мера угла АОС втрое больше, чем градусная мера угла СОВ;
б) градусная мера угла АОС на 60° больше градусной меры угла СОВ;
в) градусная мера угла АОС в 4 раза меньше, чем градусная мера угла СОВ.
Решение
а) Пусть ∠COB = x°, тогда ∠AOC = 3x°.
Сумма ∠COB + ∠AOC = ∠AOB = (x + 3х)°.
Составим уравнение:
х + 3х = 180
х = 180 : 4
х = 45°
∠COB = 45°, ∠AОС = 3 * 45 = 135°.
б) Пусть ∠COB = х°, тогда ∠AOC = (x + 60)°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + x + 60)°.
Составим уравнение:
x + х + 30 = 180
x = (180 − 60) : 2
х = 60°
∠COB = 60°, ∠AOC = 60 + 60 = 120°.
в) Пусть ∠AOC = х°, тогда ∠COB = 4х°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + 4x)°.
Составим уравнение:
х + 4х = 180
x = 180 : 5°
x = 36°
∠AOC = 36°, ∠COB = 4 * 36 = 144°.
Задание 817
Внутри прямого угла АОВ проведён луч ОС. Найдите градусные меры углов АОС и СОВ, если:
а) угол АОС в 5 раз больше угла СОВ;
б) разность градусных мер углов СОВ и АОС равна 46°;
в) угол АОС в 4 раза меньше угла СОВ.
Решение
а) Пусть ∠COB = x°, тогда ∠AOC = 5х°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + 5х) градусов.
Составим уравнение:
х + 5x = 90
х = 90 : 6
х = 15°
∠COB = 15°, LAOC = 5 * 15 = 75°.
б) Пусть ∠COB = x°, тогда ∠AOC = (90 − x)°.
Сумма ∠COB + ∠AOC = ∠AОВ = (x − (90 − x)°.
Составим уравнение:
х − (90 − х) = 46
х + х − 90 = 46
х = (46 + 90) : 2
х = 68°
∠COB = 68°, ∠AOC = 90 − 68 = 22°.
в) Пусть ∠AOC = х°, тогда ∠СОВ = 4х°.
Сумма ∠COB + ∠AOC = ∠AOB = (x + 4x)°.
Составим уравнение:
x + 4х = 90
x − 90 : 5
х = 18°
∠AOC = 18°, ∠COB = 4 * 18° = 72°.
Задание 818
Чему равна градусная мера каждого угла прямоугольника? Чему равна сумма этих градусных мер? Чему равна сумма градусных мер углов каждого из треугольников ABC и CDA (рис. 88)?
Решение
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
∠AВС + ∠BCD + ∠CDA + ∠DAB = 90° + 90° + 90° + 90° = 360°
∠ABC + ∠ВСА + ∠CAB = 180°
∠ACD + ∠CDA + ∠DAC = 180°
Задание 819
Измерьте каждый угол треугольника ACD, изображённого на рисунке 89, Найдите сумму градусных мер этих углов.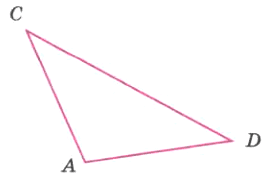
Решение
∠CAD = 110°, ∠ADC = 35°, ∠ACD = 35°
∠CAD + ∠ADC + ∠ACD = 110° + 35° + 35° = 180°
Задание 820
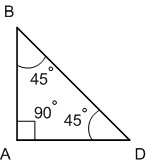
Начертите какой−нибудь треугольник и измерьте каждый его угол.
Проверьте, что сумма градусных мер углов треугольника равна 180°.
Запомните это свойство углов треугольника.
Решение
∠BAD + ∠ABD + ∠BDA = 90° + 45° + 45° = 180°
Задание 821
В треугольнике один из углов равен 75°, а другой − 80°. Чему равен третий угол этого треугольника?
Решение
180° − (75° + 80°) = 180° − 155° = 25°
Задание 822
В треугольнике ABC градусная мера угла ABC равна 40°, а градусная мера угла CAB в 3 раза больше. Найдите градусную меру угла АСВ.
Решение
∠АСВ = 180° − (∠ABC + ∠CAB) = 180° − (40° + 3 * 40°) = 180° − 160 = 20°