Ответы к странице 65

Задание 313

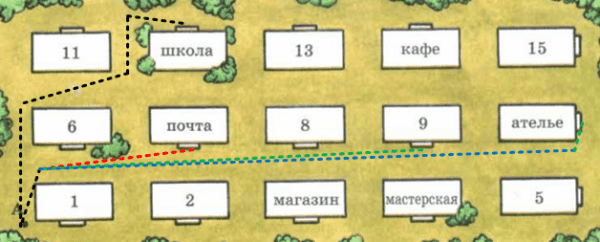
На рисунке 48 показан план квартала города. Ширина каждого дома 25 м, длина 50 м, ширина дорог 25 м. Расскажите, как ближайшим путём пройти от точки А до входа в школу; на почту; в ателье; в дом № 9. Как бы вы объяснили дорогу от дома № 5 до дома № 11; до дома № 6?

Решение

Чтобы пройти от дома № 5 до дома № 11, нужно при выходе из дома № 5 повернуть налево и идти все время прямо. После дома № 15 необходимо повернуть налево и снова идти прямо до дома № 11.

Чтобы пройти от дома № 5 до дома № 9, нужно при выходе из дома № 5 повернуть налево и еще раз налево, тем самым обогнув угол дома № 5, и идти прямо мимо ателье до дома № 9.

Задание 314

Длина прямоугольного параллелепипеда 14 см, ширина 8 см и высота 7 см. Найдите высоту другого прямоугольного параллелепипеда, если его длина 28 см, ширина 7 см, а объём равен объёму первого параллелепипеда.

Решение

1) 14 * 8 * 7 = 112 * 7 = 784 (см³) - объем первого параллелепипеда
2) 784 : (28 − 7) = 784 : 196 = 4 (см) - высота параллелепипеда, объём которого равен объёму первого
Ответ: 4 см.

Задание 315

Решите задачу:
1) Масса арбуза и трёх одинаковых дынь 10 кг. Дыня в 2 раза легче арбуза. Какова масса арбуза?
2) Масса тыквы и трёх одинаковых кабачков 20 кг. Тыква в 2 раза тяжелее кабачка. Какова масса тыквы?
3) За три прыжка кенгуру преодолел расстояние 20 м 70 см. Первые два прыжка оказались одинаковыми, а третий − на 1 м 20 см длиннее. Какова длина второго прыжка кенгуру?
4) Расстояние до норы в 6 м заяц преодолел в четыре прыжка. Первые три прыжка оказались одинаковыми, а последний на 40 см короче остальных. Найдите длину второго прыжка зайца.

Решение

1) Пусть х − масса дыни, тогда масса арбуза 2х кг.
Масса арбуза и трёх одинаковых дынь равна (3х + 2х) кг.
Составим уравнение:
3х + 2х = 10
5х = 10
х = 10 : 5
х = 2
Значит, масса дыни равна 2 кг, а масса арбуза
2х = 2 * 2 = 4 (кг)
Ответ: 4 кг.

2) Пусть у − масса кабачка, тогда масса тыквы 2у кг.
Масса тыквы и трёх одинаковых кабачков равна (3у + 2у) кг.
Составим уравнение:
3y + 2у = 20
5y = 20
у = 20 : 5
у = 4
Значит, масса кабачка 4 кг, а масса тыквы
2у = 2 * 4 = 8 (кг)
Ответ: 8 кг.

3) 20 м 70 см = 2070 см
1 м 20 см = 120 см
Пусть длина первого прыжка равна z см, длина второго z, а длина третьего прыжка (z + 120) см.
Сумма длин всех прыжков кенгуру равна (2z + z + 120) см.
Составим уравнение:
z + z + (z + 120) = 2070
3z = 1950
z = 1950 : 3
z = 650
Значит, длина второго прыжка 650 см.
Ответ: 650 см.

4) Пусть длина каждого из первых трех прыжков равна х см, тогда длина четвёртого прыжка будет (x − 40) см.
Сумма длин четырёх прыжков (3x + x − 40) см.
Составим уравнение:
3х + х − 40 = 600
4х = 600 + 40
4х = 640
х = 640 : 4
х = 160 
Значит, длина второго прыжка 160 см.
Ответ: 160 см.

Задание 316

Решите уравнение:
1) х : 16 = 4759 + 1441;
2) у : 27 = 2467 − 1867;
3) 13 600 : z = 3876 − 3851;
4) (2865 + k) * 125 = 542875.

Решение

1) x : 16 = 4759 + 1441
x : 16 = 6200
x = 6200 * 16
х = 99200

2) у : 27 = 2467 − 1867
у : 27 = 600
у = 600 * 27
у = 16200

3) 13600 : z = 3876 − 3851
13600 : z = 25
z = 13600 : 25
z = 544

4) (2865 + k) − 125 = 542875
2865 + k = 542875 : 125
2865 + k = 4343
k = 4343 − 2865
k = 1478