Ответы к странице 137
Задание 737
Решите задачу:
1) Расстояние между посёлком и городом 144 км. Сколько времени затратил человек на дорогу туда и обратно, если в город он ехал на автобусе со скоростью 36 км/ч, а возвращался на автомобиле со скоростью 72 км/ч?
2) Расстояние между пристанями 378 км. Сколько времени потребуется теплоходу, чтобы проплыть туда и обратно, если его скорость по течению реки 27 км/ч, а против течения 21 км/ч?
Решение
1) 144 : 36 + 144 : 72 = 4 + 2 = 6 (ч)
Ответ: 6 ч потребуется на весь путь.
2) 378 : 27 + 378 : 21 = 14 + 18 = 32 ч.
Ответ: 32 ч потребуется теплоходу.
Задание 738
Выполните действия:
1) (6656 : 512 + 28) * (1524 : 127 − 7) − 150;
2) (4992 : 384 − 8) * (8496 : 236 + 15) + 145.
Решение
1) (6656 : 512 + 28) * (1524 : 127 − 7) − 150 = (13 + 28) * (12 − 7) − 150 = 41 * 5 − 150 = 205 − 150 = 55
2) (4992 : 384 − 8) * (8496 : 236 + 15) + 145 = (13 − 8) * (36 + 15) + 145 = 5 * 51 + 145 = 255 + 145 = 400
Задание 739
Длина прямоугольника 65 см, а его ширина в 5 раз меньше. Чему равна площадь прямоугольника?
Решение
S = ab = 65 * (65 : 5) = 65 * 13 = 845 (см2)
Задание 740
Площадь прямоугольника 136 см2. Чему равна его длина, если его ширина 8 см?
Решение
S = ab
136 = 8а
а = 136 : 8
а = 17 (см)
Ответ: длина прямоугольника 17 см.
Задание 741
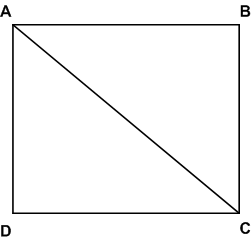
Начертите прямоугольник ABCD, соедините отрезком вершины А и С. Найдите площади треугольников ABC и ACD, если АВ = 6 см и ВС = 5 см.
Решение
S ABCD = AВ * ВС = 6 * 5 = 30 (см2)
S ABC = S ACD = 1/2 SABCD : 2 = 30 : 2 = 15 (см2 )
Задание 742
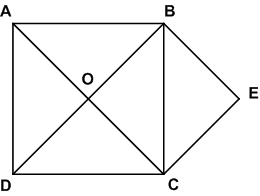
Постройте квадрат ABCD со стороной 4 см и проведите в нём отрезки АС и BD. Чему равна площадь каждого из четырёх получившихся треугольников? Сложите из двух таких треугольников новый квадрат. Чему равна его площадь?
Решение
S ABO = S BOC = S COD − S AOD = S ABCD : 4 = ( 4 * 4 ) : 4 = 16 : 4 = 4 (см2)
S OBEC = 2 * S BOC = 2 * 4 = 8 (см2 )
Задание 743
Используя формулу пути s = vt, найдите:
а) путь, который пролетит муха за 3 с, если её скорость 5 м/с;
б) время, за которое ласточка пролетит 162 км, если её скорость 54 км/ч;
в) скорость собаки, которая за 5 с пробежала 25 м.
Решение
а) s = vt
при t = 3 с, v = 5 м/с
s = 5 * 3
s = 15
Ответ: 15 м.
б) s = vt
если s = 162 км, v = 54 км/ч;
162 = 54t
t = 162 : 54
t = 3
Ответ: 3 ч.
в) s = vt
если t = 5 с, s = 25 м
25 = 5v
v = 25 : 5
v= 5
Ответ: 5 м/с.
Задание 744
Используя формулу периметра прямоугольника Р = 2(а + b), найдите:
а) периметр Р, если а = 3 м 5 дм, b = 1 м 2 дм;
б) сторону а, если Р = 3 дм, b = 6 см.
Решение
а) при a = 3 м 5 дм, b = 1 м 2 дм
Р = 2(а + b) = 2 * (35 + 12) = 2 * 47 = 94 (дм) = 9 м 4 дм
б) при Р = 3 дм, b = 6 см, Р = 2(а + b)
a = P : 2 − b = 30 : 2 − 6 = 15 − 6 = 9 (см)
Задание 745
Выразите:
а) в метрах: 5 км; 5 км 30 м; 200 дм; 30 000 см;
б) в дециметрах: 3 м; 7 м 9 дм; 500 см; 7000 м.
Решение
a) 5 км = 5000 м, 5 км 300 м = 5030 м, 200 дм = 20 м, 30000 см = 300 м.
б) 3 м = 30 дм, 7 м 9 дм = 79 дм, 500 см = 50 дм, 7000 м = 70000 дм.
!Задание 746
Выполните действия:
(38 * 216 : 57 + 3780 : 108 − 10) : 13= (8208 : 57 + 35 − 10) = (144 + 25) : 13 = 169 : 13 = 13