Ответы к странице 150

Задание 816

Найдите площадь поверхности и сумму длин рёбер куба, ребро которого 11 см.

Решение

S = 6а² = 6*11² = 6*121 = 726 (см².) - площадь поверхности куба.
L = 12а = 12 * 11 = 132 (см) - сумма длин ребер.

Задание 817

Сколько понадобится краски, чтобы покрасить поверхность бруса, изображённого на рисунке 82, если для покраски 1дм² поверхности нужно 2 г краски?

Решение

S = 2(4*3+3*2+2*4) = 2*26 = 52 (дм²) - площадь поверхности бруса.
52 * 2 = 104 (г) - краски нужно для покраски.
Ответ: 104 г краски понадобится.

Задание 818

Прямоугольный участок земли имеет длину 95 м, а ширину 67 м. Найдите площадь и периметр участка.

Решение

1) 95 * 67 = 6365 (м²) - площадь участка.
2)  (95 + 67) * 2 = 162 * 2 = 324 (м) - периметр участка.
Ответ: 6365 м², 324 м.

Задание 819

Незнайка стал догонять Шпунтика, когда расстояние между ними было равно 1 км 80 м. Незнайка бежал со скоростью 170 м/мин, а Шпунтик шёл со скоростью 80 м/мин. Через сколько минут Незнайка догонит Шпунтика?

Решение

1) 170 − 80 = 90 (м/мин) - скорость сближения.
2) 1080 : 90 = 12 (мин) - время, через которое они встретятся.
Ответ: через 12 минут Незнайка догонит Шпунтика.

!Задание 820

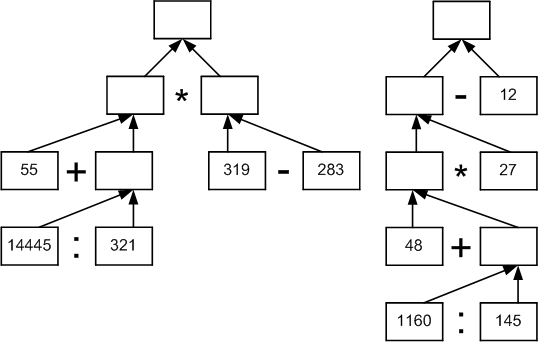
Найдите значение выражения, предварительно составив схему вычислений:
а) (55 + 14 445 : 321) * (319 − 283);
б) (48 + 1160 : 145) * 27 − 12.

Решение

а) (55 + 14445 : 321) * (319 − 283) = (55 + 45) * 36 = 100 − 36 = 3600

б) (48 + 1160 : 145) * 27 − 12 = (48 + 8) * 27 − 12 = 56 * 27 − 12 = 1512 − 12 = 1500

Задание 821

Подумайте, по какому правилу составлен ряд чисел, и найдите три следующих числа:
а) 20, 22, 24, ... ;
б) 2, 4, 8, 16, ... ;
в) 1, 3, 9, ... ;
г) 1, 4, 9, 16, ... ;
д) 2, 5, 4, 8, 6, 11, ... ;
е) 1, 8, 27, ... .

Решение

a) 20, 22, 24, 26, 28, 30, ... − каждый последующий член ряда на 2 больше предыдущего

б) 2, 4, 8, 16, 32, 64, 128, ... − каждый последующий член ряда в 2 раза больше предыдущего

в) 1, 3, 9, 27, 81, 243, ... − каждый последующий член ряда в 3 раза больше предыдущего

г) 1, 4, 9, 16, 25, 36, 49, ... − числа ряда − квадраты последовательности натуральных чисел

д) 2, 5, 4, 8, б, 11, 8, 14, 10, ... − каждый последующий член ряда с чётным номером на 2 больше предыдущего члена с чётным номером, а каждый последующий член ряда с нечётным номером на 3 больше предыдущего члена с нечётным номером

е) 1,8, 27, 64, 125, 216, ... − числа ряда − кубы последовательности натуральных чисел