Задание №1390
На рисунке 213 изображены навесная и настильная траектории полёта
снаряда. Равны ли для этих движений пройденные снарядом пути; перемещения?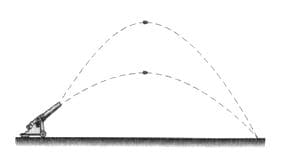 рис. 213
рис. 213
Ответ
Пути различны, перемещения одинаковы.
Задание №1391
Белка бежит внутри колеса, находясь на одной и той же высоте относительно пола. Сравните путь и перемещение при таком движении.
Ответ
Перемещение равно нулю, путь больше нуля.
Задание №1392
Спортсмену предстоит пробежать один круг (400 м). Чему равно его перемещение, если он пробежал 200 м пути; если он финишировал? Дорожку стадиона считать окружностью.
Ответ
Дано:
L = 400 м;
$l_{1} = 200$ м;
$l_{2} = 400$ м.
Найти:
$\overset{→}{s_{1}}$ − ?
$\overset{→}{s_{2}}$ − ?
Решение:
Так как длина круга равна 400 м, это значит что пробежав 200 метров спортсмен окажется ровно на противоположной стороне круга. В таком случае модуль перемещения будет равен расстоянию между стартом и местом где находится спортсмен после пробега 200 метров, т.е. перемещение будет равно диаметру руга или двум радиусам:
$\overset{→}{s_{1}}$ = d = 2r.
Длина окружности равна:
L = 2πr = πd;
$d = \frac{L}{π}$;
$d = \frac{400}{3,14} = 127,4$ м.
$\overset{→}{s_{1}}$ = 127,4 м.
Когда спортсмен финиширует, он окажется в той же точке с которой стартовал, значит модуль перемещения равен нулю.
$\overset{→}{s_{2}}$ = 0.
Ответ: 127,4 м; 0.
Задание №1393
Тело, брошенное вертикально вверх из точки А, упало в шахту (рис. 214). Чему равны пройденный телом путь и модуль перемещения, если АВ = 15 м, ВС = 18 м?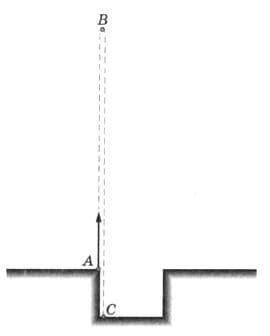 рис. 214
рис. 214
Ответ
Дано:
АВ = 15 м;
ВС = 18 м.
Найти:
s − ?
|$\overset{→}{s}$| − ?
Решение:
Пройденный путь равен:
s = AB + BC;
s = 15 + 18 = 33 м;
Модуль перемещения равен:
|$\overset{→}{s}$| = BC − AB;
|$\overset{→}{s}$| = 18 − 15 = 3 м.
Ответ: 33 м; 3 м.
Задание №1394
На рисунке 215 показана траектория движения пешехода, который пришёл из пункта А в пункт D. Определите координаты пешехода в начале и конце движения, пройденный путь, модуль перемещения.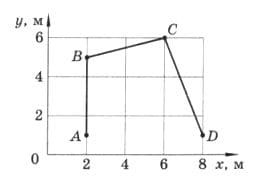 рис. 215
рис. 215
Ответ
Координаты пешехода в начале движения в точке A (2;1), в конце движения − в точке D (8;1).
Перемещение тела (материальной точки) − вектор, соединяющий начальное положение тела с его последующим положением. Чтобы найти модуль перемещения тела нужно определить кратчайшие расстояние между точками A и D. Модуль перемещения равен:
|$\overset{→}{s}$| = 8 − 2 = 6 м.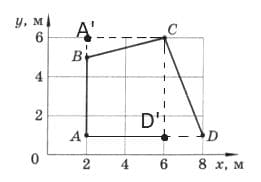 Пройденный путь равен сумме отрезков:
Пройденный путь равен сумме отрезков:
s = AB + BC + CD.
AB = 5 − 1 = 4 м;
Найдем длину отрезка BC по теореме Пифагора:
ВС = $\sqrt{A'B^{2} + CA'^{2}} = \sqrt{(6-5)^{2} + (6-2)^{2}} = 4,1$ м;
Найдем длину отрезка CD по теореме Пифагора:
CD = $\sqrt{CD'^{2} + DD'^{2}} = \sqrt{(6-1)^{2} + (8-6)^{2}} = 5,4$ м;
s = 4 + 4,12 + 5,39 = 13,5 м.
Ответ: A (2;1); D (8;1); 6 м; 13,5 м.
Задание №1395
Тело переместилось из точки с координатами $х_{1} = -2$ м, $у_{1} = 3$ м в точку с координатами $х_{2} = 2$ м, $у_{2} = 6$ м. Сделайте чертёж, найдите модуль перемещения и его проекции на оси координат.
Ответ
Дано:
$х_{1} = -2$ м;
$у_{1} = 3$ м;
$х_{2} = 2$ м;
$у_{2} = 6$ м.
Найти:
|$\overset{→}{s}$| − ?
$s_{х}$ − ?
$s_{y}$ − ?
Решение: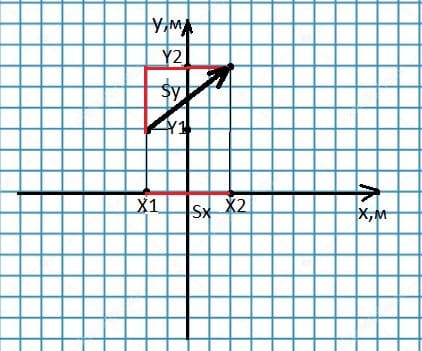 $s_{x} = x_{2} - x_{1}$;
$s_{x} = x_{2} - x_{1}$;
$s_{x} = 2 - (-2) = 4$ м;
$s_{y} = y_{2} - y_{1}$;
$s_{y} = 6 - 3 = 3$ м;
Найдем модуль перемещения по теореме Пифагора:
|$\overset{→}{s}| = \sqrt{s_{x}^{2} + s_{y}^{2}}$;
|$\overset{→}{s}| = \sqrt{4^{2} + 3^{2}} = 5$ м.
Ответ: $s_{x} = 4$ м; $s_{y} = 3$ м; |$\overset{→}{s}| = 5$ м.
Задание №1396
Начало вектора перемещения находится в точке О с координатами $х_{1} = -1$ м, $у_{1} = 2$ м. Проекция вектора перемещения на ось х равна З м, а на ось у − 4 м. Найдите графически вектор перемещения и его модуль.
Ответ
Дано:
$х_{1} = -1$ м;
$у_{1} = 2$ м;
$s_{х} = 3$ м;
$s_{y} = -4$ м.
Найти:
|$\overset{→}{s}$| − ?
Решение: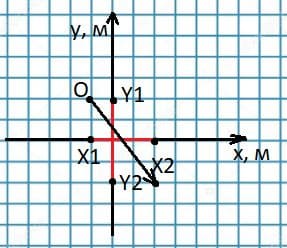 $x_{2} = x_{1} + s_{x}$;
$x_{2} = x_{1} + s_{x}$;
$x_{2} = -1 + 3 = 2$ м;
$y_{2} = y_{1} + s_{y}$;
$y_{2} = 2 + (-4) = -2$ м;
Найдем модуль перемещения по теореме Пифагора:
|$\overset{→}{s}| = \sqrt{s_{x}^{2} + s_{y}^{2}}$;
|$\overset{→}{s}| = \sqrt{3^{2} + (-4)^{2}} = 5$ м.
Ответ: |$\overset{→}{s}| = 5$ м.

