Задание №1440
Тело, двигаясь равноускоренно из состояния покоя, за третью секунду после начала движения прошло 5 м. Найдите ускорение движения и скорость тела в конце третьей секунды.
Решение
Дано:
$t_{2}$ = 2 c;
$t_{3}$ = 3 c;
$S_{t =3} = 5$ м.
Найти:
a − ?
$v_{t =3}$ − ?
Решение:
Уравнение движения:
$S = v_{0}t + \frac {at^{2}}{2}$;
Тело начинает движение, поэтому $v_{0} = 0$.
$S = \frac {at^{2}}{2}$;
За третью секунду тело прошло путь $S = S_{3} - S_{2}$, где $S_{2}$ − путь, пройденный телом за 2 секунды, $S_{3}$ − путь, пройденный телом за 3 секунды.
$S = \frac {at_{3}^{2}}{2} - \frac {at_{2}^{2}}{2} = \frac{a}{2} * (t_{3}^{2} - t_{2}^{2})$;
$a = \frac{2S}{t_{3}^{2} - t_{2}^{2}}$;
$a = \frac{2 * 5}{3^{2} - 2^{2}} = 2м/с^{2}$;
$v = v_{0} + at$;
Т.к. $v_{0} = 0$, то v = at;
v = 2 * 3 = 6 м/с.
Ответ: 2 $м/с^{2}$; 6 м/с.
Задание №1441
При равноускоренном движении с начальной скоростью 5 м/с тело за 3 с прошло 20 м. С каким ускорением двигалось тело? Чему равна его скорость в конце третьей секунды? Какой путь тело прошло за вторую секунду?
Решение
Дано:
$v_{0} = 5$ м/с;
$t_{3} = 3$ c;
S = 20 м.
Найти:
a − ?
$v_{3}$ − ?
$S_{2с}$ − ?
Решение:
Уравнение движения:
$S = v_{0}t + \frac {at^{2}}{2}$;
$S = \frac{2v_{0}t +at^{2}}{2}$;
$2S = 2v_{0}t +at^{2}$;
$at^{2} = 2S - 2v_{0}t$;
$a = \frac{2S - 2v_{0}t}{t^{2}}$;
$a = \frac{2 * 20 - 2 * 5 * 3}{3^{2}} = 1,1 м/с^{2}$;
Уравнение скорости:
$v = v_{0} + at$;
$v_{3} = 5 + 1,1 * 3 = 8,3$ м/с;
За вторую секунду тело прошло путь $S_{2c} = S_{2} - S_{1}$, где $S_{2}$ − путь, пройденный телом за 2 секунды, $S_{1}$ − путь, пройденный телом за 1 секунду.
$S_{2} = v_{0}t_{2} + \frac {at_{2}^{2}}{2} = 5 * 2 + \frac {1,1 * 2^{2}}{2} = 12,2$ м;
$S_{1} = v_{0}t_{1} + \frac {at_{1}^{2}}{2} = 5 * 1 + \frac {1,1 * 1^{2}}{2} = 5,5$ м;
$S_{2c} = 12,2 - 5,5 = 6,7$ м.
Ответ: 1,1 $м/с^{2}$; 8,3 м/с; 6,7 м.
Задание №1442
По графику скорости (рис. 231) определите:
а) начальную скорость тела;
б) скорость тела через 5 с;
в) ускорение тела;
г) путь, пройденный телом за 5 с.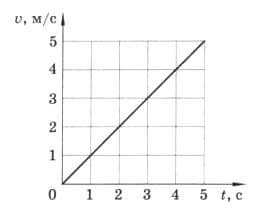 рис. 231
рис. 231
Решение
а) $v_{0} = 0$.
б) t = 5 c;
$v_{t=5} = 5$ м/с.
в) $v = v_{0} + at$;
$a= \frac{v – v _{0}}{t}$;
$a= \frac{5-0}{5} = 1 м/с^{2}$.
г) t = 5 c;
$S = v_{0}t + \frac {at^{2}}{2}$;
$S = 0 + \frac {1 * 5^{2}}{2} = 12,5$ м.
Задание №1443
По графику скорости (рис. 232) определите:
а) начальную скорость тела;
б) скорость тела через 5 с;
в) ускорение тела;
г) путь, пройденный телом за 10 с.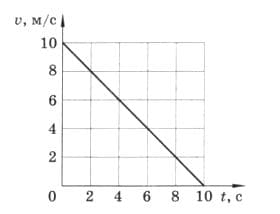 рис. 232
рис. 232
Решение
а) $v_{0} = 10$ м/с.
б) t = 5 c;
$v_{5} = 5$ м/с.
в) Уравнение скорости:
$v = v_{0} + at$;
$a= \frac{v - v _{0}}{t}$;
$a= \frac{5 - 10}{5} = - 1 м/с^{2}$.
Ответ: − 1 $м/с^{2}$.
г) t = 10 c;
$S = \frac {v_{0} + v}{2} * t$;
$S = \frac {10 + 0}{2} * 10 = 50$ м.
Ответ: 50 м.
Задание №1444
По графику скорости, изображённому на рисунке 233, определите:
а) начальную скорость тела;
б) скорость тела через 1 с;
в) ускорение тела на первой секунде пути;
г) путь, пройденный телом за 5 с.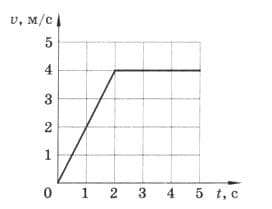 рис. 233
рис. 233
Решение
а) $v_{0} = 0$ м/с.
б) t = 1 c;
v= 2 м/с.
в) Уравнение скорости:
$v = v_{0} + at$;
$a= \frac{v - v_{0}}{t}$;
$a_{1}= \frac{2-0}{1} = 2 м/с^{2}$.
Ответ: 2 $м/с^{2}$.
г) Первые 2 секунды тело двигалось равноускоренно, потом 3 секунды равномерно.
Найдем путь, который прошло тело за 2 секунды равноускоренного движения:
$S = v_{0}t + \frac {at^{2}}{2}$;
$S_{2} = 0 + \frac {2 * 2^{2}}{2} = 4$ м;
Найдем путь, который прошло тело за 3 секунды равномерного движения:
S = vt;
$S_{3} = 4 * 3 = 12$ м;
$S = S_{2} + S_{3} = 4 + 12 = 16$ м.
Ответ: 16 м.
Задание №1445
По графику скорости, изображённому на рисунке 234, определите:
а) начальную скорость тела;
б) скорость тела через 2 с;
в) ускорение тела в первые две секунды пути;
г) ускорение тела между второй и десятой секундами пути;
д) путь, пройденный телом за 10 с.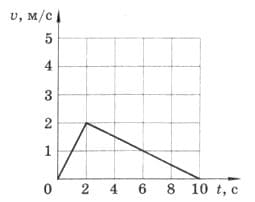 рис. 234
рис. 234
Решение
а) $v_{0} = 0$ м/с.
б) t = 2 c;
v= 2 м/с.
в) Уравнение скорости:
$v = v_{0} + at$;
$a= \frac{ v - v_{0}}{t}$;
$a_{2}= \frac{2-0}{2} = 1 м/с^{2}$.
Ответ: 1 $м/с^{2}$.
г) С 2−й по 10−ю секунду пути равнозамедленное движение.
$v_{0} = 2$ м/с;
v = 0;
t = 8 c.
Уравнение скорости:
$v = v_{0} + at$;
$a= \frac{ v - v_{0}}{t}$;
$a_{2}= \frac{0-2}{8} = -0,25 м/с^{2}$.
Ответ: −0,25 $м/с^{2}$.
д) Уравнение движения:
$S = \frac {v_{0} + v}{2} * t$;
1−й участок пути:
$S_{1} = \frac {0 + 2}{2} * 2 = 2$ м;
2−й участок пути:
$S_{2} = \frac {2 + 0}{2} * 8 = 8$ м;
$S = S_{1} + S_{2} = 2 + 8 = 10$ м.
Ответ: 10 м.

