Задание №1563

Спортсмен на Земле (g = 9,8 $м/с^{2}$) толкнул ядро на 20 м. На какое расстояние полетело бы это ядро при тех же условиях на Марсе (g = 3,7 $м/с^{2}$); на Юпитере (g = 23 $м/с^{2}$)?

Решение 1
Дано:
$g_{1} = 9,8 м/с^{2}$;
$g_{2} = 3,7 м/с^{2}$;
$l_{1} = 20$ м;
g ≈ 10 $м/с^{2}$.
Найти:
$l_{2}$ − ?
Решение: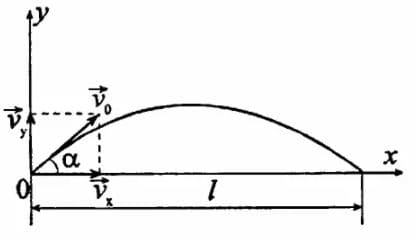
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
Т.к. $v_{0y} = v_{0}sinα$; $g_{y} = -g$; $v_{y} = 0$, то
$0 = v_{0}sinα - gt$;
$v_{0}sinα = gt$;
$t = \frac{v_{0}sinα}{g}$
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}sosα$; x = l, то:
$l = v_{0}sosα * 2t = v_{0}sosα * 2 * \frac{v_{0}sinα}{g} = \frac{2v_{0}^{2}sinsαcosα}{g}$;
Тогда
$l_{1} = \frac{2v_{0}^{2}sinsαcosα}{g_{1}}$;
$l_{2} = \frac{2v_{0}^{2}sinsαcosα}{g_{2}}$;
$\frac{l_{1}}{l_{2}} = \frac{\frac{2v_{0}^{2}sinsαcosα}{g_{1}}}{\frac{2v_{0}^{2}sinsαcosα}{g_{2}}} = \frac{g_{2}}{g_{1}} $;
$l_{2} = \frac{l_{1}g_{1}}{g_{2}}$;
$l_{2} = \frac{20 * 9,8}{3,7} = 53$ м.
Ответ: 53 м.

Решение 2
Дано:
$g_{1} = 9,8 м/с^{2}$;
$g_{2} = 23 м/с^{2}$;
$l_{1} = 20$ м;
g ≈ 10 $м/с^{2}$.
Найти:
$l_{2}$ − ?
Решение: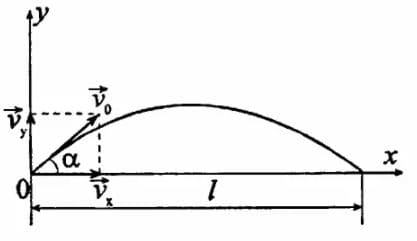
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
Т.к. $v_{0y} = v_{0}sinα$; $g_{y} = -g$; $v_{y} = 0$, то
$0 = v_{0}sinα - gt$;
$v_{0}sinα = gt$;
$t = \frac{v_{0}sinα}{g}$
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}sosα$; x = l, то:
$l = v_{0}sosα * 2t = v_{0}sosα * 2 * \frac{v_{0}sinα}{g} = \frac{2v_{0}^{2}sinsαcosα}{g}$;
Тогда
$l_{1} = \frac{2v_{0}^{2}sinsαcosα}{g_{1}}$;
$l_{2} = \frac{2v_{0}^{2}sinsαcosα}{g_{2}}$;
$\frac{l_{1}}{l_{2}} = \frac{\frac{2v_{0}^{2}sinsαcosα}{g_{1}}}{\frac{2v_{0}^{2}sinsαcosα}{g_{2}}} = \frac{g_{2}}{g_{1}} $;
$l_{2} = \frac{l_{1}g_{1}}{g_{2}}$;
$l_{2} = \frac{20 * 9,8}{23} = 8,5$ м.
Ответ: 8,5 м.

Задание №1564

Мальчик прыгает в длину. Под каким углом к горизонту совершены прыжки, если:
а) дальность полёта L больше максимальной высоты полёта Н в 3 раза;
б) L = Н?

Решение

а) Дано:
L = 3H.
Найти:
α − ?
Решение: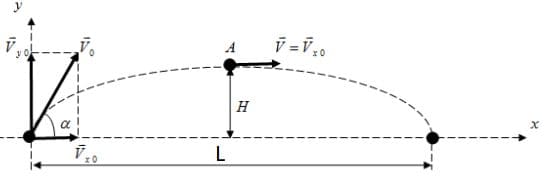
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = v_{0}sinα$; $g_{y} = -g$; y = H; $y_{0} = 0$, $v_{y} = 0$,то
$0 = v_{0}sinα - gt$;
$t = \frac{v_{0}sinα}{g}$;
$H = (v_{0}sinα)t - \frac {gt^{2}}{2} =(v_{0}sinα) * \frac{v_{0}sinα}{g} - \frac {g (\frac{v_{0}sinα}{g})^{2}}{2} = \frac{v_{0}^{2}sin^{2}α}{g} - \frac{v_{0}^{2}sin^{2}α}{2g} = \frac{2v_{0}^{2}sin^{2}α - v_{0}^{2}sin^{2}α}{2g} = \frac{v_{0}^{2}sin^{2}α}{2g}$;
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}cosα$; x = L, то:
$L = (v_{0}cosα) * 2t = (v_{0}cosα) * 2 * \frac{v_{0}sinα}{g} = \frac{2v_{0}^{2}sinαcosα}{g}$;
L = 3H;
$\frac{2v_{0}^{2}sinαcosα}{g} = \frac{3v_{0}^{2}sin^{2}α}{2g}$;
$\frac{\frac{3v_{0}^{2}sin^{2}α}{2g}}{\frac{2v_{0}^{2}sinαcosα}{g}} = 1$;
$\frac{3sinα}{4cosα} = 1$;
$tgα = \frac{4}{3} = 1,33$;
α = arctg(1,33) = 53°.
Ответ: 53°.

б) Дано:
L = H.
Найти:
α − ?
Решение:
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = v_{0}sinα$; $g_{y} = -g$; y = H; $y_{0} = 0$, $v_{y} = 0$,то
$0 = v_{0}sinα - gt$;
$t = \frac{v_{0}sinα}{g}$;
$H = (v_{0}sinα)t - \frac {gt^{2}}{2} =(v_{0}sinα) * \frac{v_{0}sinα}{g} - \frac {g (\frac{v_{0}sinα}{g})^{2}}{2} = \frac{v_{0}^{2}sin^{2}α}{g} - \frac{v_{0}^{2}sin^{2}α}{2g} = \frac{2v_{0}^{2}sin^{2}α - v_{0}^{2}sin^{2}α}{2g} = \frac{v_{0}^{2}sin^{2}α}{2g}$;
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}cosα$; x = L, то:
$L = (v_{0}cosα) * 2t = (v_{0}cosα) * 2 * \frac{v_{0}sinα}{g} = \frac{2v_{0}^{2}sinαcosα}{g}$;
L = H;
$\frac{2v_{0}^{2}sinαcosα}{g} = \frac{v_{0}^{2}sin^{2}α}{2g}$;
$\frac{\frac{v_{0}^{2}sin^{2}α}{2g}}{\frac{2v_{0}^{2}sinαcosα}{g}} = 1$;
$\frac{sinα}{4cosα} = 1$;
$tgα = 4$;
α = arctg(4) = 76°.
Ответ: 76°.

Задание №1565

Гепард − самое быстрое животное. Он развивает скорость до 90 км/ч, совершая при этом прыжки длиной до 25 м. Оцените приблизительно высоту этих прыжков.

Решение

Дано:
$v_{0} = 90$ км/ч;
L = 25 м;
g ≈ 10 $м/с^{2}$.
Найти:
H − ?
СИ:
$v_{0} = 25$ м/с.
Решение: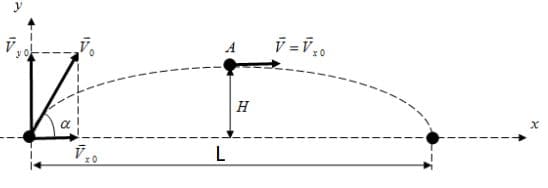
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = v_{0}sinα$; $g_{y} = -g$; y = H; $y_{0} = 0$, $v_{y} = 0$,то
$0 = v_{0}sinα - gt$;
$t = \frac{v_{0}sinα}{g}$;
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}cosα$; x = L, то:
$L = (v_{0}cosα) * 2t = (v_{0}cosα) * 2 * \frac{v_{0}sinα}{g} = \frac{2v_{0}^{2}sinαcosα}{g}$;
Т.к. 2sinαcosα = sin2α, то:
$L = \frac{v_{0}^{2}sin2α}{g}$;
$sin2α = \frac{Lg}{v_{0}^{2}}$;
$2α = arcsin (\frac{Lg}{v_{0}^{2}})$;
$α = \frac{arcsin (\frac{Lg}{v_{0}^{2}})}{2}$;
$α = \frac{arcsin (\frac{25 * 10}{25^{2}})}{2} = \frac{arcsin(0,4)}{2} = \frac{23,6}{2} = 11,8$;
$H = (v_{0}sinα)t - \frac {gt^{2}}{2} =(v_{0}sinα) * \frac{v_{0}sinα}{g} - \frac {g (\frac{v_{0}sinα}{g})^{2}}{2} = \frac{v_{0}^{2}sin^{2}α}{g} - \frac{v_{0}^{2}sin^{2}α}{2g} = \frac{2v_{0}^{2}sin^{2}α - v_{0}^{2}sin^{2}α}{2g} = \frac{v_{0}^{2}sin^{2}α}{2g}$;
$H = \frac{25^{2} * sin^{2} (11,8)}{2 * 10} = 1,3$ м.
Ответ: 1,3 м.

Задание №1566

Докажите, что при отсутствии сопротивления воздуха время $t_{1}$ поднятия тела на высоту h равно времени $t_{2}$ падения его с этой высоты.

Решение

При движении вверх тело двигается с замедлением g, пока его скорость не достигает нуля.
$v_{1} = v_{01} - gt_{1} = 0$;
$v_{01} = gt_{1}$;
Путь, пройденный телом, при движении вверх:
$h_{1} = v_{01}t_{1} - \frac {gt_{1}^{2}}{2} = gt_{1} * t_{1} - \frac {gt_{1}^{2}}{2} = \frac {2gt_{1}^{2} - gt_{1}^{2}}{2} = \frac {gt_{1}^{2}}{2}$;
$t_{1}= \sqrt{\frac{2h_{1}}{g}}$;
Путь, пройденный телом, при движении вниз:
$h_{2} = v_{02}t_{2} + \frac {gt_{2}^{2}}{2}$;
Т.к. $v_{02} = 0$, то:
$h_{2} = \frac{gt_{2}^{2}}{2}$;
$2h_{2} = gt_{2}^{2}$;
$t_{2}^{2} = \frac{2h_{2}}{g}$;
$t_{2}= \sqrt{\frac{2h_{2}}{g}}$;
Т.к. $h_{1} = h_{2}$, то
$t_{1}= \sqrt{\frac{2h}{g}}$;
$t_{2}= \sqrt{\frac{2h}{g}}$;
$t_{1} = t_{2}$.
Таким образом, при отсутствии сопротивления воздуха время $t_{1}$ поднятия тела на высоту h равно времени $t_{2}$ падения его с этой высоты.

Задание №1567

Докажите, что при отсутствии сопротивления воздуха начальная скорость $v_{0}$, тела, брошенного вертикально вверх, равна его скорости v в момент касания земли.

Решение

При движении вверх тело двигается с замедлением g, пока его скорость не достигает нуля.
$v_{1} = v_{01} - gt_{1} = 0$;
$v_{01} = gt_{1}$;
При движении вниз тело двигается с ускорением g без начальной скорости.
$v_{2} = v_{02} + gt_{2}$;
Т.к. $v_{02} = 0$, то $v_{2} = gt_{2}$;
При отсутствии сопротивления воздуха время $t_{1}$ поднятия тела на высоту h равно времени $t_{2}$ падения его с этой высоты.
Т.к. $t_{1} = t_{2} = t$, то
$v_{01} = gt$;
$v_{2} = gt$.
$v_{01} = v$.
При отсутствии сопротивления воздуха начальная скорость $v_{0}$, тела, брошенного вертикально вверх, равна его скорости v в момент касания земли.

Задание №1568

Аристотель утверждал: «Падение куска золота, или свинца, или любого другого тела, наделённого весом, происходит тем быстрее, чем больше его вес...» Ошибочность точки зрения Аристотеля доказал Галилей с помощью мысленного эксперимента, анализируя с позиции Аристотеля падение двух тел разной массы в двух случаях:
а) тела связаны друг с другом;
б) тела падают отдельно друг от друга.
Попытайтесь повторить рассуждения Галилея.

Решение

а) Пусть прав Аристотель.
Если связать тела вместе, то, с одной стороны, они должны падать быстрее более тяжёлого тела, так как масса их больше, а с другой стороны, более лёгкое тело тормозит более тяжёлое, и тела должны падать медленнее, чем одно более тяжёлое тело.
Пришли к противоречию.

б) Пусть прав Аристотель.
Если тела падают отдельно друг от друга, то более тяжёлое тело должно упасть быстрее, чем более легкое тело. Однако, чем тяжелее тело, тем его объем больше при равной плотности, и сопротивление увеличивается, значит тело большего объема будет падать медленнее.
Пришли к противоречию.

Задание №1569

В результате экспериментов Галилей пришёл к выводу о том, «...что пространства, проходимые падающим телом в одинаковые промежутки времени, относятся между собой как последовательные нечётные числа». Что следует из этого вывода учёного?

Решение

Из этого вывода следует, что свободное падение тел − равноускоренное движение.

Задание №1570

Аристотель считал: «Камень под действием собственного веса падает с определённой скоростью. Если положить на него ещё один такой же камень, то лежащий сверху будет подталкивать нижний, в результате чего скорость последнего возрастает». В чём заключается допущенная Аристотелем ошибка?

Решение

Аристотель считал, что роль положенного сверху камня сводится лишь к тому, чтобы подталкивать нижний. На самом деле ему нужно не только (вернее, не столько) приводить в движение нижний камень, сколько самого себя. Таким образом, одновременно с увеличением в 2 раза силы, приводя− щей камни в движение (это сила тяжести), ровно во столько же раз увеличивается приводимая в движение масса, а ускорение остаётся неизменным в соответствии со вторым законом Ньютона: $a = \frac{F}{m}$.

Задание №1571

Два тела, массы которых М и m (М > m), подняты на одинаковую высоту над землёй и одновременно отпущены. Исследуйте, одновременно ли они приземлятся, если сила сопротивления воздуха для обоих тел одинакова и постоянна.

Решение

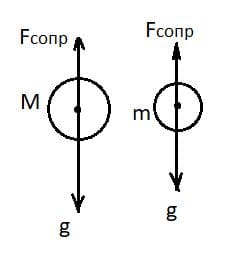Найдем ускорение тел $a_{1}$ и $a_{2}$ из второго закона Ньютона
для первого тела:
$g - F_{сопр} = Ma_{1}$;
$a_{1} = g - \frac{F_{сопр}}{M}$,
для второго тела:
$g - F_{сопр} = Ma_{2}$,
$a_{2} = g - \frac{F_{сопр}}{m}$,
$a_{1} > a_{2}$.
Ответ: Более тяжёлое тело упадёт раньше, т.к. движется с большим ускорением.

Задание №1572

Итальянский учёный Никола Тарталья (1499 − 1557) в одной из своих работ сообщил, что он «после изрядного размышления» доказал «естественными и математическими доводами» , что наибольшая дальность полёта снаряда
достигается при наклоне орудия под углом 45° к горизонту. Подтвердите математически вывод учёного.

Решение

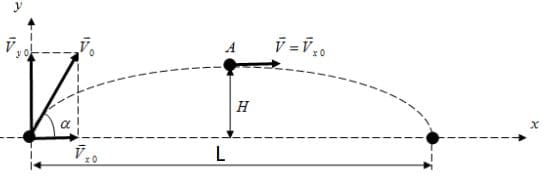Направим ось Ox параллельно горизонтальной составляющей начальной скорости, а ось Oy вверх. За начало отсчета примем точку старта снаряда.
Движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
Т.к. $v_{0y} = v_{0}sinα$; $g_{y} = -g$; $v_{y} = 0$,то
$0 = v_{0}sinα - gt$;
$t = \frac{v_{0}sinα}{g}$;
Время полета снаряда в 2 раза больше времени его подъема.
$t_{п}= 2t$;
Движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t_{п}$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}cosα$; x = L, то:
$L = (v_{0}cosα) * 2t = (v_{0}cosα) * 2 * \frac{v_{0}sinα}{g} = \frac{2v_{0}^{2}sinαcosα}{g}$;
Т.к. 2sinαcosα = sin2α, то:
$L = \frac{v_{0}^{2}sin2α}{g}$;
Дальность полёта тела при одной и тоже начальной скорости зависит от угла, под которым тело брошено к горизонту. Дальность полёта максимальная, когда максимален sin2α.
Максимальное значение синуса равно единице по угле 90°, т.е.
sin2α = 1;
2α = 90°;
α = 45°.
Ответ: 45°.