Задание №225
Измеряя удлинение пружины, ученик подвешивал к ней грузы разной массы. Полученные результаты приведены в таблице. По данным этой таблицы постройте график зависимости удлинения пружины от веса тела. По полученному графику определите, каким будет удлинение, если к пружине подвесить груз массой 600 г.
| Масса груза, кг | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| Удлинение пружины, см | 0,5 | 1 | 1,5 | 2 | 2,5 |
Решение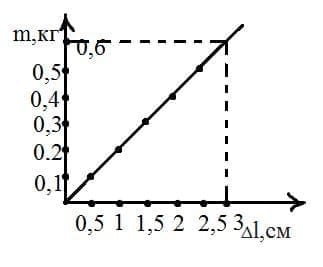 Если к пружине подвесить груз массой 600 г, то удлинение пружины равно 3 см.
Если к пружине подвесить груз массой 600 г, то удлинение пружины равно 3 см.
Задание №226
По графикам зависимости силы упругости, возникающей при растяжении, от удлинения найдите жёсткость пружин I и II (рис. 18).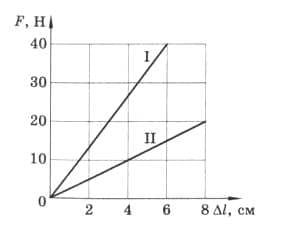 рис. 18
рис. 18
Решение
$F_{упр}=kΔl$;
$k = \frac{F_{упр}}{Δl}$;
Согласно графику сила упругости первой пружины равна 40 Н, удлинение пружины − 0,06 м. Тогда $k = \frac{40}{0,06} = 667$ Н/м.
Сила упругости второй пружины равна 20 Н, удлинение пружины − 0,08 м. Тогда $k = \frac{20}{0,08} = 250$ Н/м.
Задание №227
На рисунке 19 приведены графики зависимости силы упругости от удлинения для двух пружин. К какой из пружин − I или II − надо подвесить груз большей массы, чтобы удлинение пружин было одинаковым?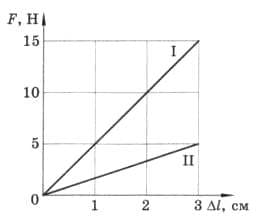
рис. 19
Решение
Чтобы получить удлинение пружины равной 3 см, нужно к пружинам приложить разные силы упругости ($F_{1}>F_{2}$). Первую пружину нужно растягивать с большей силой. Поэтому, чтобы удлинение пружин было одинаковым, груз большей массы нужно подвесить к I пружине.
Задание №228
Какую силу надо приложить к концам проволоки, жёсткость которой 1000 Н/м, чтобы растянуть её на 1 см?
Решение
Дано:
k = 1000 Н/м;
Δl = 1 см;
Найти:
$F_{упр}$ − ?
СИ:
Δl = 0,01 м.
Решение:
$F_{упр}=kΔl$;
$F_{упр} = 1000 * 0,01 = 10$ Н.
Ответ: 10 Н.
Задание №229
Шарик массой 100 г, висящий на резинке, растянул её на 1 см. Найдите жёсткость резинки.
Решение
Дано:
m = 100 г;
Δl = 1 см;
Найти:
k − ?
СИ:
m = 0,1 кг;
Δl = 0,01 м.
Решение:
Шарик воздействовует на резинку только своим весом:
$F_{упр} = F_{тяж}$;
$F_{тяж} = mg$;
g ≈10 Н/кг;
$F_{тяж} = 0,1 * 10 = 1$ Н;
$F_{упр}=kΔl$;
$k = \frac{F_{упр}}{Δl}$;
$k = \frac{1}{0,01} = 100$ Н/м.
Ответ: 100 Н/м.
Задание №230
Рассчитайте жёсткость пружины, которая под действием силы 4 Н удлинилась на 2 см.
Решение
Дано:
$F_{упр} = 4$ Н;
Δl = 2 см;
Найти:
k − ?
СИ:
Δl = 0,02 м.
Решение:
$F_{упр}=kΔl$;
$k = \frac{F_{упр}}{Δl}$;
$k = \frac{4}{0,02} = 200$ Н/м.
Ответ: 200 Н/м.
Задание №231
Под действием силы 160 Н пружина амортизатора сжалась на 4,5 мм. На сколько миллиметров сожмётся пружина при нагрузке 800 Н?
Решение
Дано:
$F_{1} = 160$ Н;
$Δl_{1} = 4,5$ мм;
$F_{2} = 800$ Н;
Найти:
$Δl_{2}$ − ?
СИ:
$Δl_{1} = 0,0045$ м.
Решение:
$F_{упр}=kΔl$;
Так как пружины одна, значит жесткость одинакова. Найдем жесткость пружины:
$k = \frac{F_{1}}{Δl_{1}}$;
$k = \frac{160}{0,0045} = 35556$ Н/м.
Найдем удлинение пружины при нагрузке 800 Н:
$Δl_{2} = \frac{F_{2}}{k}$;
$Δl_{2} = \frac{800}{35556} = 0,0225$ м = 22,5 мм.
Ответ: 22,5 мм.
Задание №232
При открывании двери длина дверной пружины увеличилась на 12 см, сила упругости пружины составила при этом 4 Н. При каком удлинении пружины сила упругости равна 10 Н?
Решение
Дано:
$F_{1} = 4$ Н;
$Δl_{1} = 12$ см;
$F_{2} = 10$ Н;
Найти:
$Δl_{2}$ − ?
СИ:
$Δl_{1} = 0,12$ м.
Решение:
$F_{упр}=kΔl$;
Так как пружины одна, значит жесткость одинакова. Найдем жесткость пружины:
$k = \frac{F_{1}}{Δl_{1}}$;
$k = \frac{4}{0,12} = 33,3$ Н/м.
Найдем удлинение пружины при нагрузке 10 Н:
$Δl_{2} = \frac{F_{2}}{k}$;
$Δl_{2} = \frac{10}{33,3} = 0,3$ м = 30 см.
Ответ: 30 см.

