Задание №1679

Одним из тренажёров, используемых для подготовки космонавтов к предстоящим полётам, является специальная центрифуга. Какую перегрузку испытывает космонавт, если центрифуга радиусом R = 6 м вращается с частотой n = 20 об/мин?

Решение

Дано:
R = 6 м;
n = 20 об/мин;
g = 9,8 $м/с^{2}$.
Найти:
k − ?
СИ:
n = 0,33 об/с.
Решение:
Перегрузка − величина, равная отношению центростремительного ускорения к ускорению свободного падения на поверхности Земли.
Найдем скорость движения центрифуги:
v = 2πRν;
Найдем центростремительное ускорение
$a_{ц} = \frac{v^{2}}{R} = \frac{4π^{2}R^{2}ν^{2}}{R} = 4π^{2}Rν^{2}$;
$a_{ц} = 4 * 3,14^{2} * 6 * 0,33^{2}= 25,77 м/с^{2}$;
$k = \frac{a_{ц}}{g} =\frac{25,77}{9,8} = 2,6$.
Ответ: 2,6.

Задание №1680

Метатель молота перед броском быстро вращается. При этом молот описывает окружность радиусом 1,4 м со скоростью 10 м/с. Масса молота 7,3 кг. С какой силой надо удерживать молот, чтобы он не вырвался из рук?

Решение

Дано:
R = 1,4 м;
v = 10 м/с;
m = 7,3 кг.
Найти:
$F_{ц}$ − ?
Решение:
Движение молота по дуге окружности является движением с центростремительным ускорением:
$a_{ц}= \frac{ν^{2}}{R}$;
При равномерном вращательном движении на вращающееся тело действует центробежная сила:
$F_{ц} = ma_{ц} = \frac{mν^{2}}{R}$;
$F_{ц} = \frac{7,3 * 10^{2}}{1,4} = 521$ Н.
Ответ: 521 Н.

Задание №1681

Два связанных нитью бруска массами $m_{1} = 150$ г и $m_{2}= 200$ г лежат на горизонтальной плоскости (рис. 258). К бруску массой $m_{1}$ приложена параллельно плоскости сила F = 7 Н. Коэффициент трения μ = 0,1. Найдите ускорение системы.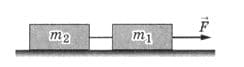

Решение
Дано:
$m_{1} = 150$ г;
$m_{2}= 200$ г;
F = 7 Н;
μ = 0,1;
g = 9,8 Н/кг.
Найти:
a − ?
СИ:
$m_{1} = 0,15$ кг;
$m_{2}= 0,2$ кг.
Решение:
Изобразим все силы, действующие на бруски: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, сила тяги $\overset{→}{F}$, сила натяжения нити $\overset{→}{T}$.
Запишем второй закон Ньютона в векторной форме для каждого бруска:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{N_{1}} + \overset{→}{F_{тр1}} + \overset{→}{F} + \overset{→}{T}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{N_{2}} + \overset{→}{F_{тр2}} + \overset{→}{T} $;
Выберем Ось X параллельно и ось Y перпендикулярно горизонтальной плоскости. Рассмотрим первое и второе уравнение в проекции на вертикальную ось:
Ось Y:
$0 = N_{1} - m_{1}g$;
$0 = N_{2} - m_{2}g$;
$N_{1} = m_{1}g$;
$N_{2} = m_{2}g$;
Рассмотрим первое и второе уравнение в проекции на горизонтальную ось:
Ось X:
$m_{1}а = F - F_{тр1} - T$;
$m_{2}а = T - F_{тр2}$;
Сложим полученные уравнения:
$m_{1}а + m_{2}а = F - F_{тр1} - F_{тр2}$;
$F_{тр1} = μN$;
$a * (m_{1} + m_{2}) = F - μN_{1} - μN_{2} = F - μm_{1}g - μm_{2}g = F - μg * (m_{1} + m_{2})$;
$a = \frac{ F - μg * (m_{1} + m_{2})}{m_{1} + m_{2}} = \frac{ F}{m_{1} + m_{2}} - μg$;
$a = \frac{7}{0,15 + 0,2} - 0,1 * 9,8 = 19 м/с^{2}$.
Ответ: 19 $м/с^{2}$.

Задание №1682

Два груза массами $m_{1} = 200$ г и $m_{2} = 300$ г связаны нитью и лежат на горизонтальной поверхности стола. С каким ускорением будет двигаться система, если к грузам приложить силы $F_{1} = 1,5$ Н и $F_{2} = 1$ Н (рис. 259)? Коэффициент трения μ = 0,05.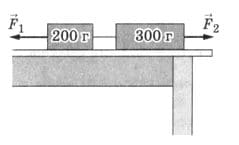
рис. 259

Решение

Дано:
$m_{1} = 200$ г;
$m_{2}= 300$ г;
$F_{1} = 1,5$ Н;
$F_{2} = 1$ Н
μ = 0,05;
g ≈ 10 Н/кг.
Найти:
a − ?
СИ:
$m_{1} = 0,2$ кг;
$m_{2}= 0,3$ кг.
Решение: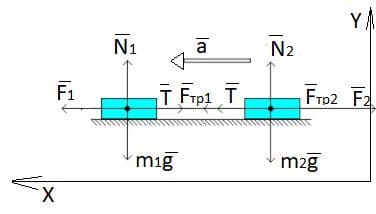
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, сила тяги $\overset{→}{F}$, сила натяжения нити $\overset{→}{T}$.
Запишем второй закон Ньютона в векторной форме для каждого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{N_{1}} + \overset{→}{F_{тр1}} + \overset{→}{F_{1}} + \overset{→}{T}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{N_{2}} + \overset{→}{F_{тр2}} + \overset{→}{F_{2}} + \overset{→}{T} $;
Выберем Ось X параллельно и ось Y перпендикулярно горизонтальной плоскости. Рассмотрим первое и второе уравнение в проекции на вертикальную ось:
Ось Y:
$0 = N_{1} - m_{1}g$;
$0 = N_{2} - m_{2}g$;
$N_{1} = m_{1}g$;
$N_{2} = m_{2}g$;
Рассмотрим первое и второе уравнение в проекции на горизонтальную ось:
Ось X:
$m_{1}а = F_{1} - F_{тр1} - T$;
$m_{2}а = T - F_{2} - F_{тр2}$;
Сложим полученные уравнения:
$m_{1}а + m_{2}а = F_{1} - F_{2} - F_{тр1} - F_{тр2}$;
$F_{тр1} = μN$;
$a * (m_{1} + m_{2}) = F_{1} - F_{2} - μN_{1} - μN_{2}$;
$a * (m_{1} + m_{2}) = F_{1} - F_{2} - μm_{1}g - μm_{2}g$;
$a * (m_{1} + m_{2}) = F_{1} - F_{2} - μg * (m_{1} + m_{2})$;
$a = \frac{F_{1} - F_{2} - μg * (m_{1} + m_{2})}{(m_{1} + m_{2})} = \frac{F_{1} - F_{2}}{m_{1} + m_{2}} - μg$;
$a = \frac{1,5 - 1}{0,2 + 0,3} - 0,05 * 10 = 0,5 м/с^{2}$.
Ответ: 0,5 $м/с^{2}$.

Задание №1683

На горизонтальной плоскости лежат два связанных нитью груза массой m каждый (рис. 260). На нити, прикреплённой к этим грузам и перекинутой через неподвижный блок, подвешен груз такой же массы. С каким ускорением движется эта система и чему равна сила натяжения нити между грузами? Трение не учитывать.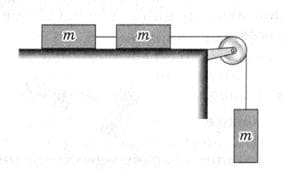
рис. 260

Решение

Дано:
$m_{1} = m_{2} = m_{3} = m$;
g ≈ 10 Н/кг.
Найти:
a − ?
$T_{1}$ − ?
$T_{2}$ − ?
Решение: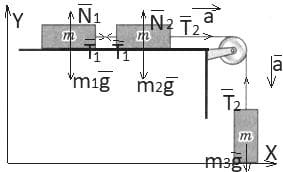
Если считать нить нерастяжимой, то тела будут двигаться как единое целое с некоторым ускорением a.
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила натяжения нити $\overset{→}{T}$.
Запишем второй закон Ньютона в векторной форме для каждого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{N_{1}} + \overset{→}{T_{1}}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{N_{2}} + \overset{→}{T_{1}} + \overset{→}{T_{2}} $;
$\overset{→}{m_{3}а} = \overset{→}{m_{3}g} + \overset{→}{T_{2}}$;
Выберем Ось X параллельно и ось Y перпендикулярно горизонтальной плоскости. Рассмотрим уравнения в проекции на вертикальную ось:
Ось Y:
$0 = N_{1} - m_{1}g$;
$0 = N_{2} - m_{2}g$;
Рассмотрим уравнения в проекции на горизонтальную ось:
Ось X:
$m_{1}а = T_{1}$;
$m_{2}а = T_{2} - T_{1}$;
$-m_{3}а = T_{2} - m_{3}g$;
Т.к. $m_{1} = m_{2} = m_{3} = m$, то
$T_{1} = mа$;
$T_{2} = mа + T_{1} = mа + mа = 2mа$;
$-mа = T_{2} - mg = 2mа - mg$;
$3mа = mg$;
$a = \frac{mg}{3m} = \frac{g}{3}$;
$a = \frac{10}{3} = 3,3 м/с^{2}$;
$T_{1} = \frac{mg}{3}$;
$T_{2} = \frac{2mg}{3}$;
Ответ: 3,3 $м/с^{2}$; $\frac{mg}{3}$; $\frac{2mg}{3}$.

Задание №1684

Два бруска, связанные между собой нитью, подвешены, как показано на рисунке 261. Какую силу $\overset{→}{F}$ нужно приложить к верхней нити, чтобы:
а) оба бруска покоились;
б) бруски двигались вверх с ускорением 1,2 $м/с^{2}$;
в) бруски двигались вниз с ускорением 1,2 $м/с^{2}$?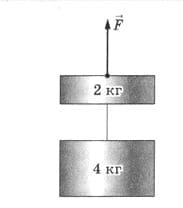
рис. 261

Решение

а) Дано:
$m_{1} = 2$ кг;
$m_{2} = 4$ кг;
g = 9,8 Н/кг.
Найти:
F − ?
Решение: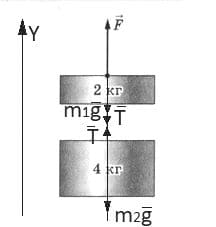
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{T}$, сила тяги $\overset{→}{F}$.
Запишем второй закон Ньютона в векторной форме для каждого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{T} + \overset{→}{F}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{T}$;
Выберем ось Y перпендикулярно горизонтальной плоскости. Рассмотрим уравнения в проекции на вертикальную ось:
Ось Y:
$0 = F - m_{1}g - T$;
$0 = T - m_{2}g$;
Сложим два уравнения:
$0 = F - m_{1}g - m_{2}g = F - g * (m_{1} + m_{2})$;
$F = g * (m_{1} + m_{2})$;
F = 9,8 * (2 + 4) = 58,8 Н.
Ответ: 58,8 Н.

б) Дано:
$m_{1} = 2$ кг;
$m_{2} = 4$ кг;
a = 1,2 $м/с^{2}$;
g = 9,8 Н/кг.
Найти:
F − ?
Решение: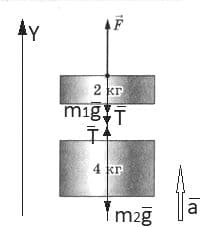
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{T}$, сила тяги $\overset{→}{F}$.
Запишем второй закон Ньютона в векторной форме для каждого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{T} + \overset{→}{F}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{T}$;
Выберем ось Y перпендикулярно горизонтальной плоскости. Рассмотрим уравнения в проекции на вертикальную ось:
Ось Y:
$m_{1}a = F - m_{1}g - T$;
$m_{2}a = T - m_{2}g$;
Сложим два уравнения:
$m_{1}a + m_{2}a = F - m_{1}g - m_{2}g$;
$F = a * (m_{1} + m_{2}) + g * (m_{1} + m_{2})$;
$F = (a + g) * (m_{1} + m_{2})$;
F = (1,2 + 9,8) * (2 + 4) = 66 Н.
Ответ: 66 Н.

в) Дано:
$m_{1} = 2$ кг;
$m_{2} = 4$ кг;
a = 1,2 $м/с^{2}$;
g = 9,8 Н/кг.
Найти:
F − ?
Решение: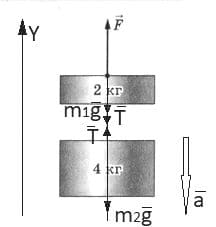
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{T}$, сила тяги $\overset{→}{F}$.
Запишем второй закон Ньютона в векторной форме для каждого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{T} + \overset{→}{F}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{T}$;
Выберем ось Y перпендикулярно горизонтальной плоскости. Рассмотрим уравнения в проекции на вертикальную ось:
Ось Y:
$-m_{1}a = F - m_{1}g - T$;
$-m_{2}a = T - m_{2}g$;
Сложим два уравнения:
$-m_{1}a - m_{2}a = F - m_{1}g - m_{2}g$;
$F = g * (m_{1} + m_{2}) - a * (m_{1} + m_{2})$;
$F = (g - a) * (m_{1} + m_{2})$;
F = (9,2 − 1,8) * (2 + 4) = 51,6 Н.
Ответ: 51,6 Н.