Задание №1420

Самолёт летит из города А в город Б и обратно со скоростью 600 км/ч относительно воздуха. Расстояние между городами 2400 км. Сколько времени займёт этот полёт:
а) в безветренный день;
б) при ветре, дующем со скоростью 36 км/ч от А к Б; от Б к А;
в) при боковом ветре (скорость его та же), перпендикулярном направлению полёта?

Решение

а) Дано:
S = 2400 км;
v = 600 км/ч.
Найти:
t − ?
Решение:
Путь самолета в прямом и обратном направлении равен:
2S = vt;
$t = \frac{2S}{v}$;
$t = \frac{2 * 2400}{600} = 8$ ч.
Ответ: 8 ч.

б) Дано:
S = 2400 км;
$v_{с} = 600$ км/ч;
$v_{в} = 36$ км/ч.
Найти:
$t_{AB}$ − ?
$t_{BA}$ − ?
Решение:
Скорость движения самолета по ветру:
$v_{1} = v_{с} + v_{в}$;
Время движение самолета по ветру:
$t_{1} = \frac{S}{v_{1}} = \frac{S}{v_{с} + v_{в}}$;
$t_{1} = \frac{2400}{600 + 36} = 3,77$ ч;
Скорость движения самолета против ветра:
$v_{2} = v_{с} - v_{в}$;
Время движения самолета против ветра:
$t_{2}= \frac{S}{v_{2}} = \frac{S}{v_{с} - v_{в}}$;
$t_{2} = \frac{2400}{600 - 36} = 4,26$ ч;
Общее время движения самолета:
$t_{AB} = 3,77 + 4,26 = 8,03$ ч.
Время движения самолета при ветре, дующем от А к Б, равно времени движения самолета при ветре, дующем от Б к А, т.к. в обоих случах одну часть пути самолет летит по ветру, другую часть − против ветра.
$t_{AB} = t_{BA} = 8,03$ ч.
Ответ: 8,03 ч.; 8,03 ч.

в) Дано:
S = 2400 км;
$v_{с} = 600$ км/ч;
$v_{в} = 36$ км/ч.
Найти:
t − ?
Решение: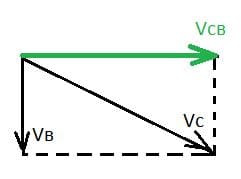
Скорость самолета при боковом ветре равна:
$v_{с}^{2} = v_{св}^{2} + v_{в}^{2}$;
$v_{св} = \sqrt{v_{с}^{2} - v_{в}^{2}}$;
$v_{св} = \sqrt{600^{2} - 36^{2}} = 598,9$ км/ч;
Путь самолета в прямом и обратном направлении равен:
$2S = v_{св}t$;
$t = \frac{2S}{v_{св}}$;
$t = \frac{2 * 2400}{598,9} = 8,01$ ч.
Ответ: 8,01 ч.

Задание №1421

Известно, что как−то знаменитому американскому математику Нейману задали каверзную задачку: «Из пунктов А и Б, отстоящих на 100 км, одновременно выходят навстречу друг другу два поезда со скоростью 50 км/ч. Как только они трогаются, пчела, устроившаяся на головной фаре поезда в пункте А, испуганно взлетает и устремляется вперёд вдоль железнодорожного полотна со скоростью 90 км/ч. Наткнувшись на поезд, идущий из пункта Б, она круто поворачивает и летит обратно с той же скоростью. Так и металась между двумя поездами, пока они не встретились. Какой путь пролетела пчела? »

Решение

Дано:
S = 100 км;
$v_{1} = v_{2} = 50$ км/ч;
$v_{пч} = 90$ км/ч.
Найти:
$S_{пч}$ − ?
Решение:
Найдём время движения поездов до встречи.
Составим уравнения движения.
$x_{1} = v_{1}t = 50t$;
$x_{2} = S - v_{2}t = 100 - 50t$.
В момент встречи, тела имеют равную координату, значит правые части уравнений можно приравнять:
50t = 100 − 50t;
100t = 100;
t = 1 ч.
Найдем путь, который пролетела пчела за время движения поездов до встречи:
$S_{пч} = v_{пч}t$;
S = 90 * 1 = 90 км.
Ответ: 90 км.

Задание №1422

Определите, сколько времени потребуется, чтобы на катере пройти расстояние 1,5 км туда и обратно по реке, скорость течения которой 2 км/ч, и по озеру (в стоячей воде), если скорость катера относительно воды в обоих случаях равна 8 км/ч.

Решение

Дано:
S = 1,5 км;
$v_{р} = 2$ км/ч;
$v_{оз} = 0$ км/ч;
$v_{к} = 8$ км/ч.
Найти:
t − ?
Решение:
Скорость движения катера по течению реки:
$v_{1} = v_{к} + v_{р}$;
Время движение катера по течению реки:
$t_{1} = \frac{S}{v_{1}} = \frac{S}{v_{к} + v_{р}}$;
$t_{1} = \frac{1,5}{8 + 2} = 0,15$ ч;
Скорость движения катера против течения реки:
$v_{2} = v_{к} - v_{р}$;
Время движение катера против течения реки:
$t_{2}= \frac{S}{v_{2}} = \frac{S}{v_{к} - v_{р}}$;
$t_{2} = \frac{1,5}{8 - 2} = 0,25$ ч;
Общее время движения катера:
t = 0,15 + 0,25 = 0,4 ч = 24 мин.
Скорость движения катера в стоячей воде озера:
$v_{3} = v_{к}$;
Время движение катера по озеру туда и обратно:
$t = \frac{2S}{v_{к}}$;
$t = \frac{2 * 1,5}{8}$ = 0,375 ч = 22,5 мин;
Ответ: 24 мин.; 22,5 мин.