Задание №1408
За 20 с до финиша положение лыжников было таким, как показано на рисунке 220. С какой скоростью двигался второй лыжник, если они пересекли линию финиша одновременно? Считать движение лыжников равномерным. Задачу решите координатным методом.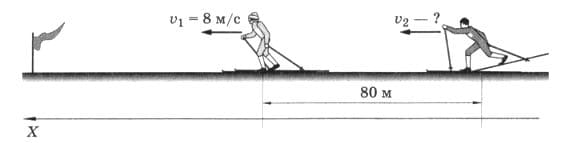 рис. 220
рис. 220
Решение
Дано:
t = 20 c;
Δs = 80 м;
$v_{1} = 8$ м/с.
Найти:
$v_{2}$ − ?
Решение:
При прямолинейном равномерном движении координата тела х(t) зависит от времени формулой: $x(t) = x_{o} + v_{x}t$, где $x_{0}$ − начальная координата тела, $v_{x}$ − скорость движения. Телом отсчета выберем первого лыжника.
Составим уравнения движения:
$x_{1} = 8t$;
$x_{2} = -80 +v_{2}t$;
Через 20 с. (на финише) тела имеют равную координату:
$х_{1 (t = 20)}= х_{2 (t = 20)}$;
Значит правые части уравнений можно приравнять:
$8t = -80 +v_{2}t$;
$8 * 20 = -80 +v_{2} * 20$;
$20v_{2} = 240$;
$v_{2} = \frac{240}{20} = 12$ м/с.
Ответ: 12 м/с.
Задание №1409
Постройте график зависимости координаты от времени, если движение тела описывается уравнением х = 2 + 5t (м). Используя полученный график, определите, какой путь прошло тело за 2 с, чему равен модуль перемещения
тела за 2 с.
Решение
Построим график зависимости координаты от времени: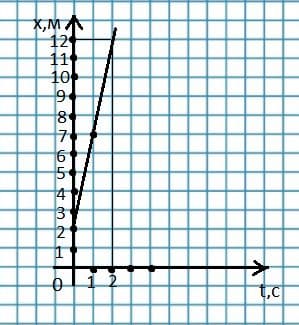 Согласно графику за 2 с тело прошло:
Согласно графику за 2 с тело прошло:
S = 10 м;
|$\overset{→}{S}$| = 10 м.
Задание №1410
Какой график зависимости пути от времени (рис. 221) соответствует равномерному движению тела? Проанализируйте каждый из приведённых графиков. Постройте графики зависимости координаты и скорости тела от времени, если тело перемещается равномерно и прямолинейно, а его движение описывается уравнением х = 3t (м).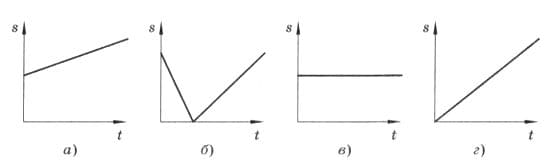 рис. 221
рис. 221
Решение
На графике г) изображено равномерное движение тела.
График а) не может изображать зависимость пути от времени, т.к. графиком, выражающим зависимость пути от времени, является прямая, выходящая из начала координат.
График б) не может изображать зависимость пути от времени, т.к. путь есть величина положительная, которая может только возрастать со временем.
На графике в) тело не движется.
х = 3t
График зависимости координаты тела от времени.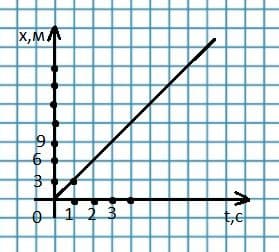 Графики зависимости скорости тела от времени.
Графики зависимости скорости тела от времени.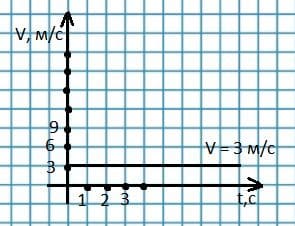
Задание №1411
На рисунке 222 изображены графики движения двух тел. Какие пути прошли эти тела за 2 с; 6 с? Напишите уравнения зависимости пути от времени.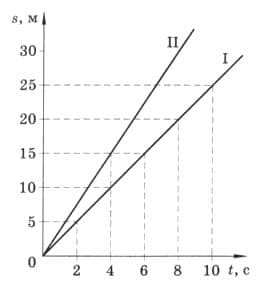 рис. 222
рис. 222
Решение
Найдем скорость движения двух тел:
S = vt;
$ v = \frac{S}{t}$;
$v_{I}= \frac{15}{6} = 2,5$ м/с;
$v_{II}= \frac{15}{4} = 3,75 м/с$.
Запишем уравнения зависимости пути от времени:
$S_{I} = v_{1}t = 2,5t$;
$S_{II} = v_{2}t = 3,75t$.
За 2 с тела прошли:
$S_{I} = 2,5 * 2 = 5$ м;
$S_{II} = 3,75 * 2 = 7,5$ м.
За 6 с тела прошли:
$S_{I} = 2,5 * 6 = 15$ м;
$S_{II} = 3,75 * 6 = 22,5$ м.
Ответ: $S_{I} = 2,5t$; $S_{II} = 3,75t$; 5 м; 7,5 м; 15 м; 22,5 м.
Задание №1412
На рисунке 223 изображены графики движения автомобиля I и трактора II, движущихся в одном направлении. Автомобиль или трактор раньше начал своё движение? Чему равны скорости автомобиля и трактора? Через какое время от начала своего движения автомобиль обгонит трактор?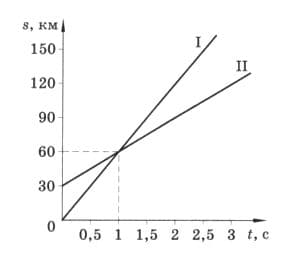 рис. 223
рис. 223
Решение
Согласно графику трактор начал движение раньше, т.к. на момент начала движения автомобиля он уже проехал 30 км.
Найдем скорость движения двух тел:
S = vt;
$v = \frac{S}{t}$;
$v_{I}= \frac{60}{1} = 60$ км/ч;
$v_{II}= \frac{30}{1} = 30$ км/ч.
Согласно графику автомобиль обгонит трактор через час от начала своего движения.
Ответ: Трактор начал движение раньше; 60 км/ч; 30 км/ч; автомобиль обгонит трактор через час от начала своего движения.
PS. На графике единица времени обозначена не корректно.

