Задание №1762

Тело брошено под углом к горизонту со скоростью $v_{0}$. Пользуясь законом сохранения механической энергии, докажите, что скорость тела на высоте Н над горизонтом определяется по формуле $v = \sqrt{v_{0}^{2} - 2 gH}$.

Решение

В момент начала движения $h_{0} = 0$, значит $E_{п} = 0$.
По закону сохранения механической энергии:
$E_{к0} = E_{п} + E_{к}$;
$\frac{mv_{0}^{2}}{2} = mgH + \frac{mv^{2}}{2}$;
$\frac{mv^{2}}{2} = \frac{mv_{0}^{2}}{2} - mgH = m * (\frac{v_{0}^{2}}{2} - gH)$;
$v^{2} = v_{0}^{2} - 2gH$;
$v = \sqrt{v_{0}^{2} - 2 gH}$.

Задание №1763

Велосипедист едет по дороге и видит, что на его пути находится препятствие − стена. Что надо сделать велосипедисту, чтобы избежать аварии − затормозить или повернуть (т.е. в каком случае он пройдёт меньшее расстояние по направлению к стене)? Учесть, что одновременно тормозить и поворачивать велосипедист не может.

Решение

Изобразим все силы, действующие на велосипедиста при повороте: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила, которая может обеспечить движение велосипедиста по окружности − сила трения $\overset{→}{F_{тр}}$.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{F_{тр}} + \overset{→}{N}$;
Спроецируем уравнение на координатные оси:
ось X: $ma = F_{тр} = μN$;
ось Y: 0 = N − mg;
N = mg;
ma = μmg;
a = μg;
Т.к. велосипедист движется по закругленной траектории, то центростремительное ускорение:
$a = \frac{v^{2}}{R} = μg$;
Радиус поворота равен:
$R = \frac{v^{2}}{μg}$;
В случае торможения, определим тормозной путь велосипедиста:
$S = \frac{v^{2}}{2a}$;
При движении по горизонтальной поверхности:
$F_{тр} = μN = μmg$;
Согласно второму закону Ньютона:
$F_{тр} = ma = μmg$;
a = μg;
$S = \frac{v^{2}}{2μg} = \frac{1}{2}R$.
Таким образом, тормозной путь будет в 2 раза меньше радиуса поворота. Велосипед лучше затормозить, а не повернуть его вдоль стены.

Задание №1764

Французский физик Мариотт провёл такой эксперимент: подвесив несколько шаров из слоновой кости на нитях равной длины так, чтобы шары соприкасались, он отклонял крайний шар и отпускал его. Этот шар наносил прямой центральный удар. Затем он отводил два шара и отпускал их. Что наблюдал при этом Мариотт? Как объяснить результат опыта? (Сделайте два рисунка: отклонён один шар, отклонены два шара. Для наглядности рассмотрите систему из четырёх шаров.)

Решение

Наблюдение:
В первом случае ударявший шар останавливался, а расположенный с противоположной стороны крайний шар отклонялся на такую же высоту.
Во втором случае останавливались два ударявших шара, а два оставшихся поднимались на такую же высоту.
Объяснение: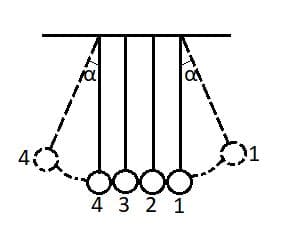
Удар шаров можно рассматривать как абсолютно упругий удар. Если при абсолютно упругом центральном ударе двух одинаковых шаров один до удара покоится, то, как известно, после удара покоившийся шар начинает двигаться со скоростью, равной той, которую имел первый шар до удара, а ранее двигавшийся шар останавливается, В нашей модели происходит ряд последовательных абсолютно упругих центральных ударов, одного шара о другой с теми же результатами. Но промежуточные шары передают свою скорость следующему и останавливаются. Так же и последний шар отходит со скоростью, которой обладал первый шар в момент удара; но поскольку он уже не встречает на пути других шаров, то поднимается на такую высоту, как и та, с которой упал правый шар (потерями энергии мы пренебрегаем).
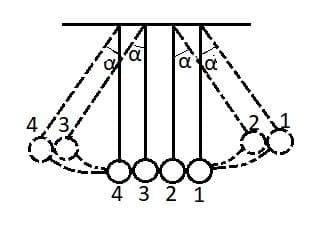Если же отвести вправо не один, а два шара и отпустить их, то они будут падать независимо один от другого. При достижении ряда шаров (3 − 4) произойдет не один удар, а последовательно два удара один за другим, т. е. сначала ударится второй о третий, а затем первый о второй. Первый из этих ударов приведет к тому, что последний свободный шар (4−й) отойдет от третьего и начнет подниматься кверху. После этого 3−й шар окажется свободным и в результате следующего удара (1−го шара) начнет подниматься кверху. Ясно, что оба эти шара (3−й и 4−й) отойдут на столько же, на сколько первоначально мы отвели 2−й и 1−й.

Задание №1765

Мальчик качается на качелях сидя. Изменится ли период колебания, если:
а) он будет качаться стоя;
б) подсядет ещё один мальчик?

Решение

а) Период колебания уменьшится, т.к. центр тяжести мальчика поднимется, и, соответственно, уменьшится длина маятника ($T = 2π\sqrt{\frac{l}{g}}$).

б) Период колебания не изменится, т.к. он не зависит от массы.

Задание №1766

Будут отставать или идти вперёд часы с секундным маятником, если их перевезти из Москвы в Архангельск; с экватора на полюс?

Решение

В обоих случаях часы будут идти вперёд.
Ускорение свободного падения в Архангельске больше, чем в Москве. Соответственно, период колебания секундного маятника в Архангельске меньше, т.к. $T = 2π\sqrt{\frac{l}{g}}$. Часы в Архангельске будут идти вперед.
Ускорение свободного падения на полюсе больше, чем на экваторе. Соответственно, период колебания секундного маятника будет меньше, т.к. $T = 2π\sqrt{\frac{l}{g}}$. Часы на полюсе будут идти вперед.

Задание №1767

Тело совершает колебания на пружине. Чему равно максимальное значение потенциальной энергии сжатой пружины, если максимальное значение кинетической энергии колеблющегося тела равно 180 Дж?

Решение

Согласно закону сохранения энергии, максимальные значения энергии равны. Максимальное значение потенциальной энергии равно 180 Дж.

Задание №1768

Самостоятельно проследите превращение энергии при колебаниях математического маятника и заполните таблицу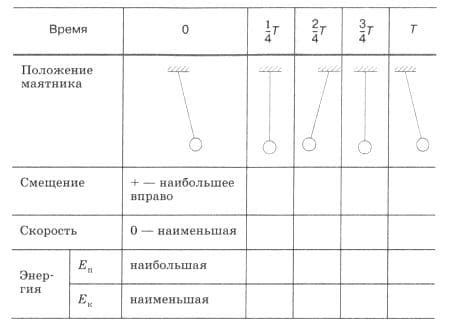

Решение
Время 0 $\frac{1}{4}T$ $\frac{2}{4}T$ $\frac{3}{4}T$ T
Смещение + − наибольшее вправо нет − наибольшее влево нет + − наибольшее вправо
Скорость 0 − наименьшая наибольшая 0 − наименьшая наибольшая 0 − наименьшая
$E_{п}$ наибольшая наименьшая наибольшая наименьшая наибольшая
$E_{к}$ наименьшая наибольшая наименьшая наибольшая наименьшая