Задание №1544
Тело брошено вертикально вверх со скоростью 20 м/с. Начертите график скорости движения данного тела. Через какое время оно упадёт на землю? Какой путь пройдёт тело при этом?
Решение
Дано:
$v_{0} = 20$ м/с;
g ≈ 10 $м/с^{2}$.
Найти:
t − ?
s − ?
Решение:
При движении вверх тело двигалось с замедлением g, пока его скорость не достигла нуля.
$v = v_{0} - gt_{1} = 0$;
$v_{0} = gt_{1}$;
$t_{1} = \frac{v_{0}}{g}$;
$t_{1} = \frac{20}{10} = 2$ с;
Путь, пройденный телом, при движении вверх:
$h_{1} = v_{0}t_{1} - \frac {gt_{1}^{2}}{2}$;
$h_{1} = 20 * 2 - \frac {10 * 2^{2}}{2} = 20$ м;
При движении вниз тело прошло такой же путь:
$h_{1} = h_{2} = 20$ м;
Таким образом, $h= 2h_{1} = 2 * 20 = 40$ м.
Найдем время падения тела:
$h_{2} = \frac{gt_{2}^{2}}{2}$;
$2h_{2} = gt_{2}^{2}$;
$t_{2}^{2} = \frac{2h_{2}}{g}$;
$t_{2}= \sqrt{\frac{2h_{2}}{g}}$;
$t_{2} = \sqrt{\frac{2 * 20}{10}} = 2$ с.
Таким образом, тело двигалось вверх и падало одинаковое время, значит:
$t = 2t_{1} = 2 * 2 = 4$ c.
Ответ: 4 с.; 40 м.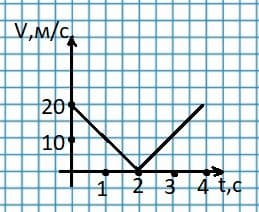
Задание №1545
Маленькая южноамериканская антилопа отталкивается от земли со скоростью 12 м/с. На какую высоту прыгает антилопа? Сколько времени длится прыжок?
Решение
Дано:
$v_{0} = 12$ м/с;
g ≈ 10 $м/с^{2}$.
Найти:
t − ?
h − ?
Решение:
При движении вверх антилопа двигалась с замедлением g, пока ее скорость не достигла нуля.
$v = v_{0} - gt_{1} = 0$;
$v_{0} = gt_{1}$;
$t_{1} = \frac{v_{0}}{g}$;
$t_{1} = \frac{12}{10} = 1,2$ с;
Высота, на которую прыгнула антилопа равна:
$h_{1} = \frac {v_{0} + v}{2} * t_{1}$;
$h_{1} = \frac {12 + 0}{2} * 1,2 = 7,2$ м;
При движении вниз антилопа прошла такой же путь. Найдем время движения антилопы вниз.
$h_{2} = \frac{gt_{2}^{2}}{2}$;
$2h_{2} = gt_{2}^{2}$;
$t_{2}^{2} = \frac{2h_{2}}{g}$;
$t_{2}= \sqrt{\frac{2h_{2}}{g}}$;
$t_{2} = \sqrt{\frac{2 * 7,2}{10}} = 1,2$ с.
Таким образом, антилопа двигалась вверх и падала одинаковое время, значит:
$t = 2t_{1} = 2 * 1,2 = 2,4$.
Ответ: 2,4 с.; 7,2 м.
Задание №1546
Тело, брошенное вертикально вверх с поверхности земли, поднимается на высоту 25 м, а затем падает на дно шахты глубиной 100 м. Через какое время от момента бросания тело достигнет дна шахты?
Решение
Дано:
$h_{1} = 25$ м;
$h_{2} = 100$ м;
g ≈ 10 $м/с^{2}$.
Найти:
t − ?
Решение:
При движении вверх тело двигалось с замедлением g, пока его скорость не достигла нуля.
$v = v_{0} - gt_{1} = 0$;
$v_{0} = gt_{1}$;
Путь, пройденный телом, при движении вверх:
$h_{1} = v_{0}t_{1} - \frac {gt_{1}^{2}}{2} = gt_{1}^{2} - \frac {gt_{1}^{2}}{2} = \frac{gt_{1}^{2}}{2}$;
$2h_{1} = gt_{1}^{2}$;
$t_{1}^{2} = \frac{2h_{1}}{g}$;
$t_{1}= \sqrt{\frac{2h_{1}}{g}}$;
$t_{1} = \sqrt{\frac{2 * 25}{10}} = 2,2$ с.
Путь, пройденный телом, при движении вниз:
$h = h_{1} + h_{2}$;
Найдем время падения тела:
$h_{1} + h_{2} = \frac{gt_{2}^{2}}{2}$;
$2 * (h_{1} + h_{2}) = gt_{2}^{2}$;
$t_{2}^{2} = \frac{2 * (h_{1} + h_{2})}{g}$;
$t_{2}= \sqrt{\frac{2 * (h_{1} + h_{2})}{g}}$;
$t_{2}= \sqrt{\frac{2 * (25 + 100)}{10}} = 5$ c;
$t = t_{1} + t_{2} = 2,2 + 5 = 7,2$ с.
Ответ: 7,2 с.
Задание №1547
На высоте 30 км двигатели метеорологической ракеты прекратили работу, сообщив ей вертикальную скорость 1 км/с. Какой наибольшей высоты достигнет ракета? На какой высоте окажется ракета через 10 с после прекращения работы двигателей?
Решение
Дано:
$h_{0} = 30$ км;
$v_{0} = 1$ км/с;
g = 10 $м/с^{2}$;
$t_{1} = 10$ c.
Найти:
h − ?
$h_{t_{1}}$ − ?
СИ:
$h_{0} = 30 000$ м.
$v_{0} = 1000$ м/с.
Решение:
При движении вверх тело двигалось с замедлением g, пока его скорость не достигла нуля.
$v = v_{0} - gt= 0$;
$v_{0} = gt$;
$t = \frac{v_{0}}{g}$;
$t = \frac{1000}{10} = 100$ с;
Путь, пройденный телом, при движении вверх:
$h = h_{0} + v_{0}t - \frac {gt^{2}}{2}$;
$h = 30000 + 1000 * 100 - \frac {10 * 100^{2}}{2} = 80 000$ м = 80 км;
$h_{t_{1}} = 30000 + 1000 * 10 - \frac {10 * 10^{2}}{2} = 39500$ м = 39,5 км.
Ответ: 80 км; 39,5 км.
Задание №1548
Каково отношение путей, пройденных телом при свободном падении:
а) за четвёртую и шестую секунды от начала движения;
б) за четыре и шесть секунд от начала движения?
Решение
а) Пути, пройденные телом за последовательно равные промежутки времени, относятся как последовательный ряд нечетных чисел 1:3:5:7:9:11 и т.д.
Таким образом, отношение путей, пройденных телом при свободном падении, за четвёртую и шестую секунды от начала движения, равно 7:11.
Или решим с помощью вычислений.
Дано:
$t_{1} = 4$ c;
$t_{2} = 6$ c;
g = 9,8 $м/с^{2}$.
Найти:
$\frac{S_{t_{1} = 4}}{S_{t_{2} = 6}}$ − ?
Решение:
$S = v_{0}t + \frac {gt^{2}}{2}$.
При падении тела без начальной скорости $v_{0} = 0$.
$S = \frac {gt^{2}}{2}$;
За четвертую секунду тело прошло путь $S_{t_{1} = 4} = S_{4} - S_{3 }$, где $S_{4}$ − путь, пройденный телом за 4 секунды, $S_{3}$ − путь, пройденный телом за 3 секунды.
$S_{t_{1} = 4} = \frac {gt_{4c}^{2}}{2} - \frac {gt_{3c}^{2}}{2} = \frac{g}{2} * (t_{4c}^{2} - t_{3c}^{2}) = \frac{9,8}{2} * (4^{2} - 3^{2}) = 34,3$ м;
За шестую секунду тело прошло путь $S_{t_{2} = 6} = S_{6} - S_{5}$, где $S_{6}$ − путь, пройденный телом за 6 секунды, $S_{5}$ − путь, пройденный телом за 5 секунды.
$S_{t_{2} = 6} = \frac {gt_{6c}^{2}}{2} - \frac {gt_{5c}^{2}}{2} = \frac{g}{2} * (t_{6c}^{2} - t_{5c}^{2}) = \frac{9,8}{2} * (6^{2} - 5^{2}) = 53,9$ м;
$\frac{S_{t_{1} = 4}}{S_{t_{2} = 6}} = \frac{34,3}{53,9} = \frac{7}{11}$.
Ответ: Отношение путей, пройденных телом при свободном падении, за четвёртую и шестую секунды от начала движения, равно 7:11.
б) Дано:
$t_{1} = 4$ c;
$t_{2} = 6$ c.
Найти:
$\frac{S_{4}}{S_{6}}$ − ?
Решение:
$S = v_{0}t + \frac {gt^{2}}{2}$.
При падении без начальной скорости $v_{0} = 0$.
$S = \frac {gt^{2}}{2}$;
За $t_{1}$, тело пройдет путь $S_{4} = \frac {g * t_{1}^{2}}{2}$;
За $t_{2}$, тело пройдет путь $S_{6} = \frac {g * t_{2}^{2}}{2}$;
$\frac{S_{4}}{S_{6}} = \frac{\frac {g * t_{1}^{2}}{2}}{\frac {g * t_{2}^{2}}{2}}=\frac{ t_{1}^{2}}{ t_{2}^{2}}$;
$\frac{S_{4}}{S_{6}} = \frac{\frac {g * 4^{2}}{2}}{\frac {g * 6^{2}}{2}} = \frac{16}{36} = \frac{4}{9}$.
Ответ: Отношение путей, пройденных телом при свободном падении, за четыре и шесть секунд от начала движения, равно 4:9.
Задание №1549
С вертолёта, находящегося на высоте 300 м, сбросили груз. Через какое время груз упадёт на землю, если:
а) вертолёт неподвижен;
б) вертолёт равномерно поднимается со скоростью 5 м/с;
в) вертолёт равномерно опускается со скоростью 5 м/с?
Сопротивлением воздуха пренебречь.
Решение
а) Дано:
h = 300 м;
g ≈ 10 $м/с^{2}$.
Найти:
t − ?
Решение:
Уравнение движения:
$h = v_{0}t + \frac {gt^{2}}{2}$;
Так как груз падает без начальной скорости, то $v_{0} = 0$;
$h = \frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
$t = \sqrt{\frac{2 * 300}{10}} = 7,7$ с.
Ответ: 7,7 с.
б) Дано:
h = 300 м;
$v_{0} = -5$ м/с;
g ≈ 10 $м/с^{2}$.
Найти:
t − ?
Решение:
Уравнение движения:
$h = v_{0}t + \frac {gt^{2}}{2}$;
$300 = -5t + 5t^{2}$;
$5t^{2} - 5t - 300 = 0$ |разделим на 5;
$t^{2} - t - 60 = 0$;
Формула дискриминанта:
a = 1; b = −1; с = −60;
$D = b^{2} - 4ac = (-1)^{2} - 4 * 1 * (-60) = 241$.
Корни уравнения:
$t_{1} = \frac{-b + \sqrt{b^{2} - 4ac}}{2a}$;
$t_{1} = \frac{-(-1) + \sqrt{241}}{2 * 1} = 8,3$ с (подходит);
$t_{2} = \frac{-b - \sqrt{b^{2} - 4ac}}{2a}$;
$t_{1} = \frac{-(-1) - \sqrt{241}}{2 * 1} = -7,3$ с (не подходит).
Ответ: 8,3 с.
в) Дано:
h = 300 м;
$v_{0} = 5$ м/с;
g ≈ 10 $м/с^{2}$.
Найти:
t − ?
Решение:
Уравнение движения:
$h = v_{0}t + \frac {gt^{2}}{2}$;
$300 = 5t + 5t^{2}$;
$5t^{2} + 5t - 300 = 0$ |разделим на 5;
$t^{2} + t - 60 = 0$;
Формула дискриминанта:
a = 1; b = 1; с = −60;
$D = b^{2} - 4ac = (1)^{2} - 4 * 1 * (-60) = 241$.
Корни уравнения:
$t_{1} = \frac{-b + \sqrt{b^{2} - 4ac}}{2a}$;
$t_{1} = \frac{-1 + \sqrt{241}}{2 * 1} = 7,3$ с (подходит);
$t_{2} = \frac{-b - \sqrt{b^{2} - 4ac}}{2a}$;
$t_{1} = \frac{-1 - \sqrt{241}}{2 * 1} = -8,3$ с (не подходит).
Ответ: 7,3 с.
Задание №1550
На каком расстоянии от цели вертолёт должен сбросить груз, если вертолёт летит на высоте 80 м с горизонтальной скоростью 108 м/с?
Решение
Дано:
h = 80 м;
v = 108 м/с;
g ≈ 10 $м/с^{2}$.
Найти:
l − ?
Решение: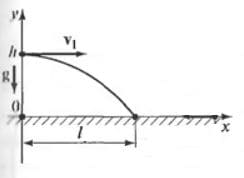 Ось Оx направлена в сторону начальной скорости груза, которая равна скорости вертолета, ось Оy направлена вертикально вверх и проходит через точку, из которой сброшен груз.
Ось Оx направлена в сторону начальной скорости груза, которая равна скорости вертолета, ось Оy направлена вертикально вверх и проходит через точку, из которой сброшен груз.
Уравнение движения груза:
$s = v_{0}t + \frac {gt^{2}}{2}$;
Проекция на координатные оси:
$x - x_{0} = v_{0x}t + \frac {g_{x}t^{2}}{2}$;
$y - y_{0} = v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0x} = v$; $v_{0y} = 0$; $g_{x} = 0$; $g_{y} = -g$; $x_{0} = 0$; $y_{0} = h$, то
x = vt;
$y = h - \frac {gt^{2}}{2}$;
В момент падения груза y = 0;
$0 = h - \frac {gt^{2}}{2}$;
$h = \frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
За это время груз проходит в горизонтальном направлении расстояние:
$l = v * \sqrt{\frac{2h}{g}}$;
$l = 108 * \sqrt{\frac{2 * 80}{10}} = 432$ м.
Ответ: 432 м.
Задание №1551
С обрыва высотой 45 м горизонтально брошено тело. Определите скорость бросания, если дальность полёта равна высоте бросания; больше высоты бросания в 2 раза. Изменится ли время полёта тела при увеличении скорости бросания?
Решение
Дано:
h = l = 45 м;
g ≈ 10 $м/с^{2}$.
Найти:
$v_{0}$ − ?
Решение: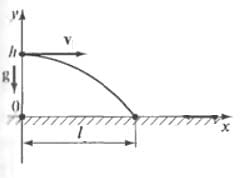 Ось Оx направлена в сторону начальной скорости тела, ось Оy направлена вертикально вверх и проходит через точку, из которой сброшено тело.
Ось Оx направлена в сторону начальной скорости тела, ось Оy направлена вертикально вверх и проходит через точку, из которой сброшено тело.
Уравнение движения тела:
$s = v_{0}t + \frac {gt^{2}}{2}$;
Проекция на координатные оси:
$x - x_{0} = v_{0x}t + \frac {g_{x}t^{2}}{2}$;
$y - y_{0} = v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0x} = v_{0}$; $v_{0y} = 0$; $g_{x} = 0$; $g_{y} = -g$; $x_{0} = 0$; $y_{0} = h$, то
$x = v_{0}t$;
$y = h - \frac {gt^{2}}{2}$;
В момент падения тела y = 0;
$0 = h - \frac {gt^{2}}{2}$;
$h = \frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
$t = \sqrt{\frac{2 * 45}{10}} = 3$ c;
За это время тело проходит в горизонтальном направлении расстояние:
$l = v_{0}t$;
$v_{0} = \frac{l}{t}$;
$v_{0} = \frac{45}{3} = 15$ с.
Ответ: 15 м/с.
Дано:
h = 45 м;
l = 2h;
g ≈ 10 $м/с^{2}$.
Найти:
$v_{0}$ − ?
Решение:
Ось Оx направлена в сторону начальной скорости тела, ось Оy направлена вертикально вверх и проходит через точку, из которой сброшено тело.
Уравнение движения тела:
$s = v_{0}t + \frac {gt^{2}}{2}$;
Проекция на координатные оси:
$x - x_{0} = v_{0x}t + \frac {g_{x}t^{2}}{2}$;
$y - y_{0} = v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0x} = v_{0}$; $v_{0y} = 0$; $g_{x} = 0$; $g_{y} = -g$; $x_{0} = 0$; $y_{0} = h$, то
$x = v_{0}t$;
$y = h - \frac {gt^{2}}{2}$;
В момент падения тела y = 0;
$0 = h - \frac {gt^{2}}{2}$;
$h = \frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
$t = \sqrt{\frac{2 * 45}{10}} = 3$ c;
За это время тело проходит в горизонтальном направлении расстояние:
$l = v_{0}t$;
$v_{0} = \frac{l}{t} = \frac{2h}{t}$;
$v_{0} = \frac{2 * 45}{3} = 30$ с.
Ответ: 30 м/с.
Из формулы $t = \sqrt{\frac{2h}{g}}$ видно, что время полёта тела не зависит от начальной скорости. Таким образом, при увеличении скорости бросания время полёта не изменится.
Задание №1552
Для определения скорости пули при выходе из ствола винтовку устанавливают горизонтально (рис. 248) и измеряют смещение пули d. Какой получен результат, если l = 35 м, d = 2,5 см.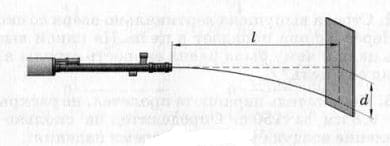 рис. 248
рис. 248
Решение
Дано:
l = 35 м;
g ≈ 10 $м/с^{2}$;
d = 2,5 см.
Найти:
$v_{0}$ − ?
СИ:
d = 0,025 м.
Решение: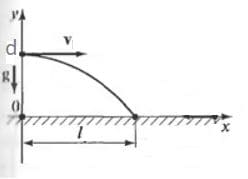 Ось Оx направлена в сторону начальной скорости тела, ось Оy направлена вертикально вверх и проходит через точку, из которой вылетает пуля из ствола.
Ось Оx направлена в сторону начальной скорости тела, ось Оy направлена вертикально вверх и проходит через точку, из которой вылетает пуля из ствола.
Уравнение движения тела:
$s = v_{0}t + \frac {gt^{2}}{2}$;
Проекция на координатные оси:
$x - x_{0} = v_{0x}t + \frac {g_{x}t^{2}}{2}$;
$y - y_{0} = v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0x} = v_{0}$; $v_{0y} = 0$; $g_{x} = 0$; $g_{y} = -g$; $x_{0} = 0$; $y_{0} = d$, то
$x = v_{0}t$;
$y = d - \frac {gt^{2}}{2}$;
В момент падения пули y = 0;
$0 = d - \frac {gt^{2}}{2}$;
$d = \frac {gt^{2}}{2}$;
$2d = gt^{2}$;
$t^{2} = \frac{2d}{g}$;
$t = \sqrt{\frac{2d}{g}}$;
За это время тело проходит в горизонтальном направлении расстояние:
$l = v_{0}t$;
$v_{0} = \frac{l}{t} = \frac{l}{\sqrt{\frac{2d}{g}}} = {l}{\sqrt{\frac{g}{2d}}}$;
$v_{0} = {35}{\sqrt{\frac{10}{2 * 0,025}}} = 495$ м/с;
Ответ: 495 м/с.

