Задание №1672
Вниз по наклонной плоскости скользит брусок: его устанавливают в положении А, а затем в положении В (рис. 257). Одинаковая ли сила трения действует на брусок в обоих случаях?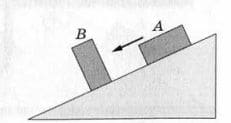 рис. 257
рис. 257
Решение
Сила трения, которая действует на бруски, одинакова в обоих случаях, т.к. сила трения не зависит от площади соприкасающихся поверхностей.
Задание №1673
Какие сани скатятся с наклонной плоскости быстрее − с грузом или без груза? Почему?
Решение
 Обозначим угол наклона плоскости через α.
Обозначим угол наклона плоскости через α.
Изобразим все силы, действующие на сани: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
$F_{тр} = μN$;
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}}$;
Выберем Ось X параллельно и ось Y перпендикулярно наклонной плоскости. Спроецируем уравнение на координатные оси:
ось Y: 0 = N − mgcosα;
$N = mgcosα$;
ось X:$ ma = mgsinα - F_{тр} = mgsinα - μN = mgsinα - μ * mgcosα = mg * (sinα - μcosα)$;
Решая систему этих уравнений получаем, что ускорение саней равно:
$a = g * (sinα - μcosα)$ и не зависит от массы, а значит, оно не изменится при увеличении массы груза.
Если не изменяется ускорение, с которым сани скатываются с наклонной плоскости, значит не изменится и время спуска.
Ответ: Сани скатятся с наклонной плоскости за одинаковое время, т.к. ускорение саней не зависит от массы груза.
Задание №1674
Почему конькобежец во время соревнований наклоняется в сторону поворота? Кто больше наклоняется − спринтеры, бегущие дистанцию 500 м, или стайеры на дистанции 10 000 м? Почему?
Решение
На конькобежца действуют силы: сила тяжести, сила реакции опоры, сила трения. Их равнодействующая при повороте конькобежца должна быть направлена к центру окружности, по которой движется спортсмен. Это возможно, если его корпус наклонен в сторону поворота.
Спринтеры, бегущие дистанцию 500 м, наклоняются больше для того, чтобы возникла сила, увеличивающая ускорения при повороте, тогда можно будет повернуть на большей скорости.
Задание №1675
На гладкой наклонной плоскости длиной 2 м и высотой 1 м лежит груз массой 100 кг. С какой силой груз давит на наклонную плоскость? Какую силу необходимо приложить к грузу, чтобы удержать его на наклонной плоскости? Как изменится модуль этой силы, если поверхность шероховатая и коэффициент трения равен 0,1?
Решение
Дано:
l = 2 м;
h = 1 м;
m = 100 кг;
g ≈ 10 Н/кг;
μ = 0,1.
Найти:
P − ?
$F_{1}$ − ?
$F_{2}$ − ?
Решение: Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Запишем второй закон Ньютона в векторной форме (для случая, когда поверхность гладкая, $\overset{→}{F_{тр}}$ = 0):
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N}$;
Выберем Ось X параллельно и ось Y перпендикулярно наклонной плоскости. Спроецируем уравнение на координатные оси:
ось X: ma = mgsinα;
ось Y: 0 = N − mgcosα;
Найдем угол наклона поверхности:
$sinα = \frac{h}{l} = \frac{1}{2} = 0,5$;
$cosα = \frac{\sqrt{l^{2} - h_{2}}}{l} = \frac{\sqrt{3}}{2} = 0,87$;
Найдем силу реакции опоры N и соответственно вес тела P:
N = P = mgcosα;
P = 100 * 10 * 0,87 = 870 Н.
Найдем силу, которую необходимо приложить к грузу, чтобы удержать его на наклонной плоскости:
$F_{1} = ma = 100 * 10 * 0,5 = 500$ Н.
Запишем второй закон Ньютона в векторной форме, если на тело действует сила трения:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}}$;
ось X:$ ma = mgsinα - F_{тр} = mgsinα - μN = mgsinα - μ * mgcosα = mg * (sinα - μcosα)$;
$F_{2} = 100 * 10 * (0,5 - 0,1 * 0,87) = 413$ Н.
Ответ: 870 Н; 500 Н; 413 Н.
Задание №1676
С каким ускорением скользит тело по наклонной плоскости с углом наклона α = 30° при коэффициенте трения μ = 0,2?
Решение
Дано:
α = 30°;
g ≈ 10 Н/кг;
μ = 0,2.
Найти:
a − ?
Решение: Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}}$;
Выберем Ось X параллельно и ось Y перпендикулярно наклонной плоскости. Спроецируем уравнение на координатные оси:
ось X: $ma = mgsinα - F_{тр}$;
ось Y: 0 = N − mgcosα;
Найдем силу реакции опоры N;
N = mgcosα;
Найдем ускорение тела:
$ma = mgsinα - F_{тр} = mgsinα - μN = mgsinα - μ * mgcosα = mg * (sinα - μcosα)$;
$a = \frac{mg * (sinα - μcosα)}{m} = g * (sinα - μcosα)$;
$a = 10 * (sin30 - 0,2 * cos30) = 3,3 м/с^{2}$.
Ответ: 3,3 $м/с^{2}$.
Задание №1677
Длина наклонной плоскости 4 м, угол наклона к горизонту 60°. За какое время соскользнёт с этой плоскости тело, если коэффициент трения равен 0,2?
Решение
Дано:
l = 4 м;
α = 60°;
g ≈ 10 Н/кг;
μ = 0,2.
Найти:
t − ?
Решение: Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}}$;
Выберем Ось X параллельно и ось Y перпендикулярно наклонной плоскости. Спроецируем уравнение на координатные оси:
ось X: $ma = mgsinα - F_{тр}$;
ось Y: 0 = N − mgcosα;
Найдем силу реакции опоры N;
N = mgcosα;
Найдем ускорение тела:
$ma = mgsinα - F_{тр} = mgsinα - μN = mgsinα - μ * mgcosα = mg * (sinα - μcosα)$;
$a = \frac{mg * (sinα - μcosα)}{m} = g * (sinα - μcosα)$;
Уравнение равноускоренного движения:
$l = v_{0}t + \frac {at^{2}}{2}$;
Т.к. тело начинает движение, то $v_{0} = 0$:
$l = \frac {at^{2}}{2}$;
$2l = at^{2}$;
$t^{2} = \frac{2l}{a}$;
$t = \sqrt{\frac{2l}{a}} = \sqrt{\frac{2l}{g * (sinα - μcosα)}}$;
$t = \sqrt{\frac{2 * 4}{10 * (sin60 - 0,2 * cos60)}} = 1$ с.
Ответ: 1 с.
Задание №1678
Тело массой 1 т поднимают по настилу с углом наклона 30° силой 7 кН. Коэффициент трения равен 0,1. Определите ускорение движения тела.
Решение
Дано:
m = 1 т;
α = 30°;
F = 7 кН;
g ≈ 10 Н/кг;
μ = 0,1.
Найти:
a − ?
СИ:
m = 1000 кг;
F = 7 000 Н.
Решение: Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, сила тяги $\overset{→}{F}$.
Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, сила тяги $\overset{→}{F}$.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}} + \overset{→}{F}$;
Выберем Ось X параллельно и ось Y перпендикулярно наклонной плоскости. Спроецируем уравнение на координатные оси:
ось X: $ma = F - F_{тр} + mgsinα $;
ось Y: 0 = N − mgcosα;
Найдем силу реакции опоры N;
N = mgcosα;
Найдем ускорение тела:
$ma = F - F_{тр} + mgsinα = F - μN + mgsinα= F- μ * mgcosα + mgsinα = F - mg * (μcosα + sinα)$;
$a = \frac{F - mg * (μcosα + sinα)}{m}$;
$a = \frac{7000 - 1000 * 10 (0,1 * cos30 + sin30)}{1000} = 1,1м/с^{2}$.
Ответ: 1,1 $м/с^{2}$.

