Задание №459
Динамометр показывает при взвешивании тела в воздухе 4,3 Н, а в воде − 1,6 Н. Определите объём тела.
Решение
Дано:
$P_{1} = 4,3$ Н;
$P_{2} = 1,6$ Н;
$ρ_{в} = 1000 кг/м^{3}$;
Найти:
V − ?
СИ:
m = 14 000 кг.
Решение:
$F_{A} = P_{1} - P_{2} = 4,3 - 1,6 = 2,7$ Н;
$F_{A} = gρ_{в}V$;
$V = \frac{F_{A}}{gρ_{в}}$;
g = 9,8 Н/кг;
$V = \frac{2,7}{9,8 * 1000} = 0,00028м^{3} = 280 см^{3}$.
Ответ: 280 $см^{3}$.
Задание №460
Бетонная плита массой 4,4 т имеет объём 2 $м^{3}$. Какая необходима сила, чтобы удержать эту плиту в воде?
Решение
Дано:
m = 4,4 т;
V = 2 $м^{3}$;
$ρ_{в} = 1000 кг/м^{3}$;
Найти:
F − ?
СИ:
m = 4400 кг.
Решение:
На бетонную плиту в воде действуют сила Архимеда (вверх), сила тяжести (вниз) и поднимающая сила (вверх).
Чтобы поднять плиту в воде должно выполняться неравенство:
$F + F_{A} > F_{тяж}$;
$F > F_{тяж} - F_{A}$;
$F_{A} = gρ_{в}V$;
$F_{тяж} = mg$;
$F = mg - gρ_{в}V$;
g = 9,8 Н/кг;
F = 4400 * 9,8 − 9,8 * 1000 * 2 = 23520 Н = 23,5 кН.
Ответ: 23,5 кН.
Задание №461
Пробковый пояс весом 20 Н имеет объём 10 $дм^{3}$. Какая требуется сила, чтобы удержать этот пояс полностью погружённым в воду? Как направлена эта сила?
Решение
Дано:
P = 20 Н;
V = 10 $дм^{3}$;
$ρ_{в} = 1000 кг/м^{3}$;
Найти:
F − ?
СИ:
V = 0,01 $м^{3}$.
Решение:
На пояс в воде действуют сила Архимеда (вверх), сила тяжести (вниз) и удерживающая сила (вниз).
Чтобы удержать пояс в воде должно выполняться условие:
$F_{A} = F_{тяж} + F$;
$F = F_{А} - F_{тяж}$;
$F_{A} = gρ_{в}V$;
$F_{тяж} = P$;
$F = gρ_{в}V - P$;
g = 9,8 Н/кг;
F = 9,8 * 1000 * 0,01 − 20 = 78 Н.
Ответ: 78 Н.
Задание №462
На сколько легче человек в воздухе, чем в безвоздушном пространстве? Объём человека принять равным 60 $дм^{3}$.
Решение
Дано:
V = 60 $дм^{3}$;
$ρ_{в} = 1,29 кг/м^{3}$;
Найти:
ΔP − ?
СИ:
V = 0,06 $м^{3}$.
Решение:
В воздухе на человека действует выталкивающая сила, направленная вверх, поэтому его вес уменьшится на величину этой силы.
$ΔP = F_{A} = gρ_{в}V$;
g = 9,8 Н/кг;
ΔP = 9,8 * 1,29 * 0,06 = 0,76 Н.
Ответ: 0,76 Н.
Задание №463
На тело объёмом 1 $дм^{3}$ действует при погружении в жидкость выталкивающая сила 6,96 Н. Какая это жидкость?
Решение
Дано:
V = 1 $дм^{3}$;
$F_{A} = 6,96$ Н.
Найти:
$ρ_{ж}$ − ?
СИ:
V = 0,001 $м^{3}$.
Решение:
$F_{A} = gρ_{ж}V$;
$ρ_{ж} = \frac{F_{A}}{gV}$
g = 9,8 Н/кг;
$ρ_{ж} = \frac{6,96}{9,8 * 0,001} = 710 кг/м^{3}$ − бензин.
Ответ: Бензин.
Задание №464
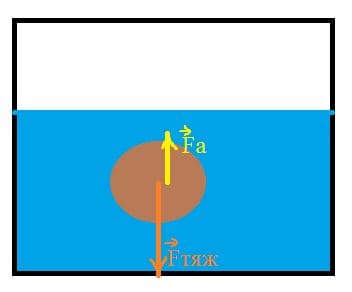
Вес тела 6 Н, его объём 400 $см^{3}$. Потонет ли тело в воде? Почему? Изобразите действующие на тело силы.
Решение
Дано:
P = 6 Н;
V = 400 $см^{3}$;
$ρ_{в} = 1000 кг/м^{3}$.
Найти:
$ρ_{т} > ρ_{в}$ − ?
СИ:
V = 0,0004 $м^{3}$.
Решение:
P = mg;
$m = ρ_{т}V$;
$P = ρ_{т}Vg$;
$ρ_{т} = \frac{P}{Vg}$;
g = 9,8 Н/кг;
$ρ_{т} = \frac{6}{0,0004 * 9,8} = 1530 кг/м^{3}$.
$ρ_{т} > ρ_{в}$, значит тело утонет.
Ответ: Тело утонет.
Задание №465
Тело объёмом 2,5 $дм^{3}$ весит в воздухе 24 Н. Потонет ли тело в воде; керосине? Ответы обоснуйте.
Решение
Дано:
P = 24 Н;
V = 2,5 $дм^{3}$;
$ρ_{в} = 1000 кг/м^{3}$;
$ρ_{к} = 800 кг/м^{3}$;
Найти:
$ρ_{т} > ρ_{в}$ − ?
$ρ_{к} > ρ_{в}$ − ?
СИ:
V = 0,0025 $м^{3}$.
Решение:
P = mg;
$m = ρ_{т}V$;
$P = ρ_{т}Vg$;
$ρ_{т} = \frac{P}{Vg}$;
g = 9,8 Н/кг;
$ρ_{т} = \frac{24}{0,0025 * 9,8} = 980 кг/м^{3}$.
$ρ_{т} ≈ ρ_{в}$, значит тело плавает.
$ρ_{т} > ρ_{к}$, значит тело потонет.
Ответ: В воде будет плавать, в керосине потонет.
Задание №466
Какого веса груз может удержать на поверхности воды пробковый пояс объёмом 8,4 $дм^{3}$, если пояс будет погружён в воду полностью; наполовину?
Решение
Дано:
$V_{1}$= 8,4 $дм^{3}$;
$V_{2} = \frac{V_{1}}{2}$;
$ρ_{в} = 1000 кг/м^{3}$;
$ρ_{пр} = 200 кг/м^{3}$.
Найти:
$P_{гр1}$ − ?
$P_{гр2}$ − ?
СИ:
V = 0,0084 $м^{3}$.
Решение:
Если тело плавает, то:
$F_{А} = P_{гр} + P_{пр}$;
$P_{гр} = F_{А} - P_{пр}$;
$F_{А} = gρ_{в}V$;
$P_{пр} = mg = gρ_{пр}V$;
Если пояс будет погружён в воду полностью, то:
$P_{гр1} = gρ_{в}V_{1} - gρ_{пр}V_{1} = gV_{1} * (ρ_{в} -ρ_{пр})$;
g = 9,8 Н/кг
$P_{гр1} = 0,0084 * 9,8 * (1000 - 200) = 66$ Н;
Если пояс будет погружён в воду наполовину, то:
$P_{гр2} = gρ_{в} * \frac{V_{1}}{2} - gρ_{пр}V_{1} = gV_{1} * (\frac{ρ_{в}}{2} - ρ_{пр})$;
$P_{гр2} = 0,0084 * 9,8 * (\frac{1000}{2} - 200) = 25$ Н.
Ответ: 66 Н; 25 Н.
Задание №467
Какая требуется сила, чтобы удержать в воде мраморную плиту массой 1000 кг?
Решение
Дано:
m = 1000 кг;
$ρ_{в} = 1000 кг/м^{3}$;
$ρ_{мр} = 2700 кг/м^{3}$;
Найти:
F − ?
СИ:
m = 4400 кг.
Решение:
На бетонную плиту в воде действуют сила Архимеда (вверх), сила тяжести (вниз) и поднимающая сила (вверх).
Чтобы поднять плиту в воде должно выполняться неравенство:
$F + F_{A} > F_{тяж}$;
$F > F_{тяж} - F_{A}$;
$m = ρ_{мр}V$;
$V = \frac{m}{ρ_{мр}}$;
$F_{A} = gρ_{в}V = \frac{mgρ_{в}}{ρ_{мр}}$;
$F_{тяж} = mg$;
$F = F_{тяж} - F_{A} = mg - \frac{mgρ_{в}}{ρ_{мр}} = mg * (1 - \frac{ρ_{в}}{ρ_{мр}})$;
g = 9,8 Н/кг;
$F = 1000 * 9,8 * (1 - \frac{1000}{2700}) = 6174$ Н ≈ 6,2 кН.
Ответ: 6,2 кН.
Задание №468
Железный якорь при погружении в воду становится легче на 120 Н. Определите объём якоря и его вес в воде.
Решение
Дано:
ΔP = 120 Н;
$ρ_{в} = 1000 кг/м^{3}$;
$ρ_{ж} = 7800 кг/м^{3}$;
Найти:
V − ?
$P_{в}$ − ?
Решение:
Сила Архимеда, действующая на тело в воде, равна разности весов.
$F_{A} = ΔP$;
$F_{А} = gρ_{в}V$;
$V = \frac{F_{А}}{gρ_{в}} = \frac{ΔP}{gρ_{в}}$;
g = 9,8 Н/кг;
$V = \frac{120}{9,8 * 1000} = 0,012 м^{3}$;
$P_{возд} = mg = ρ_{ж}Vg$;
$P_{возд} = 7800 * 0,012 * 9,8 = 917$ Н;
$P_{в} = P_{возд} - F_{A}= 917 - 120 = 797$ Н.
Ответ: 0,012 $м^{3}$; 797 Н.
Задание №469
Стальной пароходный винт весит в воздухе 8000 Н. Определите вес винта в воде.
Решение
Дано:
$P_{1} = 8000$ Н;
$ρ_{в} = 1000 кг/м^{3}$;
$ρ_{ст} = 7800 кг/м^{3}$;
Найти:
$P_{2}$ − ?
Решение:
$P_{2} = P_{1} - F_{A}$;
Р = mg;
$m = ρ_{ст}V$;
$Р =ρ_{ст}Vg$;
$ V = \frac{P}{ρ_{ст}g}$;
$F_{А} = gρ_{в}V = \frac{Pgρ_{в}}{ρ_{ст}g} = P * \frac{ρ_{в}}{ρ_{ст}}$;
$F_{А} = 8000 * \frac{1000}{7800} = 1026$ Н;
$P_{2} = 8000 - 1026 = 6974$ Н ≈ 7 кН.
Ответ: 7 кН.
Задание №470
Спортсмен способен развить силу до 800 Н. Сможет ли он удержать в воде медное тело, которое весит в воздухе 890 Н?
Решение
Дано:
F = 800 Н;
$P_{возд} = 890$ Н;
$ρ_{в} = 1000 кг/м^{3}$;
$ρ_{м} = 8900 кг/м^{3}$;
Найти:
$F > P_{в}$ − ?
Решение:
$P_{в} = P_{возд} - F_{A}$;
$F_{A} = gρ_{в}V$;
$P_{возд} = mg = gρ_{м}V$;
$V=\frac{P_{возд}}{gρ_{м}}$;
$F_{A} = gρ_{в} * \frac{P_{возд}}{gρ_{м}} = P_{возд} * \frac{ρ_{в}}{ρ_{м}}$;
$F_{A} = 890 * \frac{1000}{8900} = 100$ Н;
$P_{в} = 890 - 100 = 790$ Н;
$F > P_{в}$, следовательно, спортсмен сможет удержать в воде медное тело. Ему поможет выталкивающая сила, равная 100 Н.
Ответ: Сможет.
Задание №471
Трос лебёдки выдерживает нагрузку 25 кН. Можно ли на этом тросе поднять в воде бетонную плиту объёмом 1,5 $м^{3}$?
Решение
Дано:
F = 25 кН;
V = 1,5 $м^{3}$;
$ρ_{в} = 1000 кг/м^{3}$;
$ρ_{б} = 2200 кг/м^{3}$;
Найти:
$F > P_{в}$ − ?
СИ:
F = 25000 Н;
Решение:
$P_{в} = P_{возд} - F_{A}$;
$P_{возд} = mg = gρ_{б}V$;
$F_{A} = gρ_{в}V$;
g = 9,8 Н/кг;
$P_{в} = gρ_{б}V - gρ_{в}V = gV * (ρ_{б} - ρ_{в}) = 9,8 * 1,5 * (2200 - 1000) = 17640$ Н;
25000 Н > 17640 Н, трос лебедки весом 25 000 Н сможет поднять в воде бетонную плиту весом 17640 Н.
Ответ: Сможет.

