Задание №1747

Из ружья массой 4 кг при выстреле вылетает пуля массой 9 г со скоростью 500 м/с. На какое расстояние сместится охотник массой 80 кг при отдаче ружья, если он стоит на льду, а коэффициент трения равен 0,05?

Решение

Дано:
$m_{1} = 9$ г;
$v_{1}^{'} = 500$ м/с;
$m_{2} = 4$ кг;
$m_{3} = 80$ кг;
μ‎ = 0,05.
Найти:
S − ?
СИ:
$m_{2} = 0,009$ кг;
Решение:
По закону сохранения импульса:
$m_{1}v_{1} + m_{2}v_{2} = m_{1}v_{1}^{'} + (m_{2} + m_{3}) * v_{2}^{'} $;
В проекции на ось X:
$0 + 0 = m_{1}v_{1}^{'} - (m_{2} + M) * v_{2}^{'} $;
$m_{1}v_{1}^{'} = (m_{2} + m_{3}) * v_{2}^{'} $;
$v_{2}^{'} = \frac{m_{1}v_{1}^{'}}{m_{2} + m_{3}}$;
Начальная кинетическая энергия стрелка с ружьем составит:
$E_{к}= \frac{(m_{2} + m_{3})v_{2}^{2}}{2} = \frac{(m_{2} + m_{3)}( \frac{m_{1}v_{1}^{'}}{m_{2} + m_{3}})^2}{2} = \frac{(m_{2} + m_{3}) * m_{1}^{2}v_{1}'^{2}}{2 * (m_{2} + m_{3})^{2}} = \frac{m_{1}^{2}v_{1}'^{2}}{2 * (m_{2} + m_{3})}$;
За счет этой энергии будет совершена работа А по преодолению силы трения $F_{тр}$:
$F_{тр} = μN = μ * (m_{2} + m_{3})g$;
$A = F_{тр} * S= μgS(m_{2} + m_{3})$;
Работа равна изменению энергии. Для выполнения работы будет использован весь запас кинетической энергии:
E = A;
$\frac{m_{1}^{2}v_{1}'^{2}}{2 * (m_{2} + m_{3})} = μgS(m_{2} + m_{3})$;
$S = \frac{\frac{m_{1}^{2}v_{1}'^{2}}{2 * (m_{2} + m_{3})} }{ μg(m_{2} + m_{3})} = \frac{m_{1}^{2}v_{1}'^{2}}{2μg(m_{2} + m_{3})^{2}}$;
$S = \frac{0,009^{2} * 500'^{2}}{2 * 0,05 * 10(4 + 80)^{2}} = 2,9$ мм.
Ответ: 2,9 мм.

Задание №1748

Пружина детского пистолета, жёсткость которой 102 Н/м, имеет длину 15 см. На какую высоту поднимется шарик массой 10 г, выпущенный из пистолета вертикально вверх, если пружина пистолета была сжата до 5 см? Сопротивлением воздуха пренебречь.

Решение

Дано:
k = 102 Н/м;
$l_{1} = 15$ см;
$l_{2} = 5$ см;
m = 10 г;
g ≈ 10 Н/кг.
Найти:
h − ?
СИ:
$l_{1} = 0,15$ м;
$l_{2} = 0,05$ м;
m = 0,01 кг.
Решение:
Найдем потенциальную энергию сжатой пружины:
$E_{п}= \frac{kx^{2}}{2} = \frac{k * (l_{1} - l_{2})^{2}}{2}$;
$E_{п}= \frac{102 * (0,15 - 0,5)^{2}}{2} = 0,51$ Дж;
По закону сохранения энергии потенциальная энергия при выстреле сначала перейдет в кинетическую энергию шарика, а потом в потенциальную энергию шарика, то есть:
$E_{п} = mgh$;
$h = \frac{E_{п}}{mg}$;
$h = \frac{0,51}{0,01 * 10} = 5,1$ м.
Ответ: 5,1 м.

Задание №1749

Поезд метро, двигаясь со скоростью 72 км/ч, в точке А отключает двигатель и подходит к точке В со скоростью 54 км/ч. Определите длину участка АВ, если коэффициент сопротивления движению равен 0,01.

Решение

Дано:
$v_{1} = 72$ км/ч;
$v_{2} = 54$ км/ч;
μ = 0,01;
$g ≈ 10 м/с^{2}$.
Найти:
s − ?
СИ:
$v_{1} = 20$ м/с;
$v_{2} = 15$ м/с.
Решение: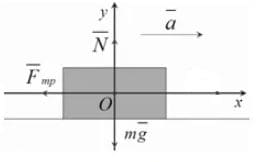
Изобразим все силы, действующие на поезд: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}}$;
Выберем Ось X параллельно и ось Y перпендикулярно горизонтальной плоскости. Спроецируем уравнение на координатные оси:
ось X:$ ma = - F_{тр}$;
ось Y: 0 = N − mg;
N = mg;
$ma = - F_{тр} = -μN = -μmg$;
$a = \frac{-μmg}{m} = -μg$;
Найдем расстояние, которое проехал поезд:
$S = \frac{v_{2}^{2} - v_{1}^{2}}{2a} = \frac{v_{2}^{2} - v_{1}^{2}}{-2μg}$;
$S = \frac{15^{2} - 20^{2}}{-2 * 0,01 * 10} = 875$ м.
Ответ: 875 м.

Задание №1750

Трамвай массой 12 т движется с постоянной скоростью 15 км/ч. На каком расстоянии от остановки необходимо начать торможение? Через какое время трамвай остановится? Силу сопротивления движению принять равной 18 кН.

Решение

Дано:
m = 12 т;
$v_{0} = 15$ км/ч;
$v_{1} = 0$ км/ч;
$F_{сопр} = 18$ кН;
$g ≈ 10 м/с^{2}$.
Найти:
s − ?
t − ?
СИ:
m = 12 000 кг;
$v_{0} = 4,2$ м/с;
$F_{сопр} = 18000$ Н.
Решение:
Изобразим все силы, действующие на трамвай: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, направленную противоположно скорости движения.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}}$;
Выберем Ось X параллельно и ось Y перпендикулярно горизонтальной плоскости. Спроецируем уравнение на ось X:
$ ma = - F_{тр}$;
$a = \frac{- F_{тр}}{m}$;
Найдем расстояние, которое проехал поезд до остановки:
$S = \frac{v_{1}^{2} - v_{0}^{2}}{2a} = \frac{v_{1}^{2} - v_{0}^{2}}{2 * \frac{- F_{тр}}{m}} = \frac{m * (v_{1}^{2} - v_{0}^{2})}{- 2F_{тр}}$;
$S = \frac{12000 * (4,2^{2} - 0^{2})}{ - 2 * 180000} =5,9$ м.
Найдем время до остановки:
$S = \frac {v_{0} + v_{1}}{2} * t$;
$t = \frac{S}{\frac {v_{0} + v_{1}}{2}} = \frac{2S}{v_{0} + v_{1}}$;
$t = \frac{2 * 5,9}{0 + 4,2} = 2,8$ с.
Ответ: 2,8 с.

Задание №1751

Масса ребёнка вместе с санками 20 кг. Коэффициент трения санок о снег 0,1.
а) Какую работу должна совершить сила, направленная вдоль наклонной плоскости, чтобы втащить санки на горку длиной 100 м и углом наклона 30°?
б) Чему будет равна скорость санок у основания наклонной плоскости, если дать им свободно скатываться вниз?

Решение

а) Дано:
m = 20 кг;
μ = 0,1;
l = 100 m;
α = 30°;
g ≈ 10 Н/кг.
Найти:
A − ?
Решение:
Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила трения $\overset{→}{F_{тр}}$, сила тяги $\overset{→}{F}$.
Запишем второй закон Ньютона в векторной форме:
$0 = \overset{→}{mg} + \overset{→}{N} + \overset{→}{F_{тр}} + \overset{→}{F}$;
Выберем Ось X параллельно и ось Y перпендикулярно наклонной плоскости. Спроецируем уравнение на координатные оси:
ось Y: 0 = N − mgcosα;
ось X:$ 0 = F - mgsinα - F_{тр} = F - mgsinα - μN= F - mgsinα - μ * mgcosα = F - mg * (sinα + μcosα)$;
F = mg * (sinα + μcosα);
Найдем работу силы тяги:
A = Fl = mgl * (sinα + μcosα);
A = 20 * 10 * 100 * (sin30 + 0,1 * cos30) = 20 000 * (0,5 + 0,087) = 11740 Дж ≈ 11,7 кДж;
Ответ: 11,7 кДж.

б) Дано:
m = 20 кг;
μ = 0,1;
l = 100 m;
α = 30°;
g ≈ 10 Н/кг.
Найти:
v − ?
Решение:
Сила трения равна:
$F_{тр} = μN = μmgcosα$;
Работа силы трения равна:
$A = F_{тр}l = μmglcosα$;
На вершине тело имеет потенциальную энергию:
$E_{п} = mgh$;
По закону сохранения энергии, соскальзывая тело расходует потенциальную энергию и приобретает кинетическую:
$E_{п} = E_{к} + A$;
$E_{к} = E_{п} - A$ = mgh − μmglcosα = mg * (h − μlcosα );
$\frac{mv^{2}}{2} = mg * (h - μlcosα )$;
$mv^{2} = 2mg * (h - μlcosα )$;
$v^{2} = \frac{2mg * (h - μlcosα)}{m} = 2g * (h - μlcosα) $;
$v = \sqrt{2g * (h - μlcosα)}$;
Т.к. h = lsinα, то:
$v = \sqrt{2g * (lsinα - μlcosα)} = \sqrt{2gl * (sinα - μcosα)}$;
$v = \sqrt{2 * 10 * 100 * (sin30 - 0,1 * cos30) = 2 000 * (0,5 - 0,087)} = 28,7$ м/с.
Ответ: 28,7 м/с.

Задание №1752

Прыгун в воду отталкивается от трамплина и приобретает скорость 5 м/с. Определите скорость входа в воду спортсмена, если высота трамплина равна 5 м.

Решение

Дано:
h = 5 м;
$v_{0} = 5$ м/с.
Найти:
v − ?
Решение:
По закону сохранения механической энергии:
$E_{п1} + E_{к1} = E_{к2}$;
$E_{п1} = mhg$;
$E_{к}= \frac{mv^{2}}{2}$;
$mhg + \frac{mv_{0}^{2}}{2} = \frac{mv^{2}}{2}$;
$\frac{mv^{2}}{2} - \frac{mv_{0}^{2}}{2} = mhg$;
$\frac{m}{2} * (v^{2} - v_{0}^{2}) = mhg$;
$v^{2} - v_{0}^{2} = \frac{mhg}{\frac{m}{2}} = 2hg$;
$v^{2} = 2hg + v_{0}^{2}$;
$v = \sqrt{2hg + v_{0}^{2}}$;
$v = \sqrt{2 * 5 * 10 + 5^{2}} = 11,2$ м/с.
Ответ: 11,2 м/с.

Задание №1753

Тело массой m соскальзывает с полусферы радиусом R (рис. 273). Найдите силу давления тела на поверхность полусферы в положении М, соответствующем углу α. На какой высоте h от вершины тело оторвётся от поверхности полусферы? Трение не учитывать.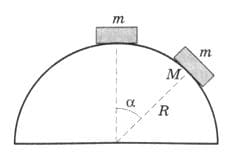
рис. 273

Решение

Дано:
m;
R;
α.
Найти:
$F_{д}$ − ?
h − ?
Решение: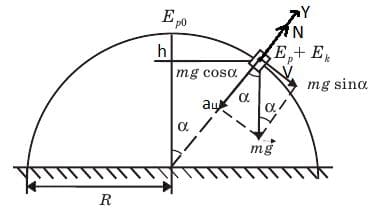
Для нахождения высоты h нам требуется определить линейную скорость тела V. Для этого воспользуемся вторым законом Ньютона. В момент отрыва тела от поверхности полусферы на него действует только сила тяжести , а сила реакции опоры становится равной нулю. Допустим это произойдет в момент, когда прямая, соединяющая тело и центр полусферы, составляет с вертикалью угол α. Запишем второй закон Ньютона в проекции на ось y, которая совпадает с упомянутой прямой.
$−mg * cosα + N = – ma_{ц}$;
$a_{ц} = \frac{v^{2}}{R}$;
Т.к. N = 0, то
$mg * cosα = \frac{mv^{2}}{R}$;
$mv^{2} = Rmgcosα$;
$v^{2} = \frac{ Rmgcosα}{m} = Rgcosα$;
По закону сохранения механической энергии потенциальная энергия тела на вершине полусферы, т.е. на высоте, равной радиусу полусферы R, равна сумме его потенциальной и кинетической энергий в любой другой точке, и значит, и в момент отрыва тела на высоте h:
$E_{п0} = E_{п} + E_{к}$;
$E_{п0} = mgR$;
$E_{п} = mgRcosα$;
$E_{к} = \frac{mv^{2}}{2}$;
$mgR = mgRcosα + \frac{mv^{2}}{2}$;
$\frac{mv^{2}}{2} = mgR - mgRcosα = mgR * (1 - cosα)$;
$mv^{2} = 2mgR * (1 - cosα)$;
$v^{2} = \frac{2mgR * (1 - cosα)}{m} = 2gR * (1 - cosα)$;
Найдем силу давления тела на поверхность полусферы в положении М:
$F_{д} = N = mg * cosα – ma_{ц} = mg * cosα – m * \frac{v^{2}}{R} = mg * cosα – \frac{m}{R} * 2gR * (1 - cosα)= mg * (cosα - 2 * (1 - cosα)) = mg * (cosα - 2 + 2cosα)) = mg * (3cosα - 2)$ ;
Найдем высоту h от вершины, на уровне которой тело оторвётся от поверхности полусферы:
$v^{2} = Rgcosα = 2gR * (1 - cosα)$;
Rgcosα = 2gR − 2gRcosα;
3Rgcosα = 2gR;
$cosα = \frac{2gR}{3gR} = \frac{2}{3}$;
$h = R - Rcosα = R - \frac{2}{3}R = \frac{1}{3}R$.
Ответ: $mg * (3cosα - 2); \frac{1}{3}R$.

Задание №1754

Галилей установил, что при скатывании шара с различных по длине и углу наклона плоскостей, имеющих одну и ту же высоту, шар имел одну и ту же скорость у основания наклонной плоскости. Объясните этот результат опыта.

Решение

По закону сохранения механической энергии:
$E_{п1} + E_{к1} = E_{п2} + E_{к2}$;
Кинетическая энергия в начальной точке и потенциальная энергия в конечной точке равны нулю, т.е. при соскальзывании потенциальная энергия тела вблизи пола полностью переходит в кинетическую энергию. Значит:
$E_{п1} = E_{к2}$;
$mgh = \frac{mv^{2}}{2}$;
$2mgh = mv^{2}$;
$v^{2} = \frac{2mgh}{m} = 2gh$;
$v = \sqrt {2gh}$.
Таким образом, скорость у основания наклонной плоскости зависит от высоты наклонной плоскости. При одинаковой высоте, скорость вблизи пола одинакова.