Ответы к странице 19
64. Какое наименьшее значение и при каких значениях a и b принимает выражение (a − 2)(a + 2) + 4b(b − a)?
Решение:
$(a - 2)(a + 2) + 4b(b - a) = a^2 - 4 + 4b^2 - 4ab = (a^2 - 4ab + 4b^2) - 4 = (a - 2b)^2 - 4$
наименьшее значение при:
a − 2b = 0
a = 2b
тогда:
$(a - 2b)^2 - 4 = (2b - 2b)^2 - 4 = 0 - 4 = -4$
Ответ: наименьшее значение −4 при a = 2b.
65. Расстояние от села Вишневое до железнодорожной станции на 14 км меньше расстояния от села Яблоневое до той же станции. Время, за которое автобус преодолевает расстояние от села Вишневое до станции, составляет 45 мин, а время, за которое легковой автомобиль проезжает от села Яблоневое до станции, на 5 мин больше, причем скорость автомобиля на 12 км/ч больше скорости автобуса. Найдите скорость автобуса и скорость легкового автомобиля.
Решение:
45 мин = $\frac{45}{60} ч = \frac{3}{4} ч$ − время, за которое автобус преодолевает расстояние от села Вишневое до станции;
(45 + 5) мин = 50 мин = $\frac{50}{60} ч = \frac{5}{6} ч$ − время, за которое автомобиль преодолевает расстояние от села Яблоневое до станции.
Пусть x км/ч − скорость автобуса, тогда
v t S
Автобус x км/ч $\frac{3}{4}$ ч $\frac{3}{4}x$ км
Автомобиль x + 12 км/ч $\frac{5}{6}$ ч $\frac{5}{6}(x + 12)$ км
Зная, что расстояние от села Вишневое до железнодорожной станции на 14 км меньше расстояния от села Яблоневое до той же станции, можно составить уравнение:
$\frac{5}{6}(x + 12) - \frac{3}{4}x = 14$
$\frac{5}{6}x + 10 - \frac{3}{4}x = 14$
$\frac{10}{12}x - \frac{9}{12}x = 14 - 10$
$\frac{1}{12}x = 4$
x = 4 * 12
x = 48 (км/ч) − скорость автобуса;
x + 12 = 60 (км/ч) − скорость автомобиля.
Ответ:
48 (км/ч) − скорость автобуса;
60 (км/ч) − скорость автомобиля.
66. Выполните действия:
1) $\frac{7}{18} + \frac{5}{18}$;
2) $\frac{9}{16} + \frac{7}{16}$;
3) $\frac{23}{32} - \frac{15}{32}$;
4) $4 - 1\frac{3}{11}$.
Решение:
1) $\frac{7}{18} + \frac{5}{18} = \frac{12}{18} = \frac{2}{3}$
2) $\frac{9}{16} + \frac{7}{16} = \frac{16}{16} = 1$
3) $\frac{23}{32} - \frac{15}{32} = \frac{8}{32} = \frac{1}{4}$
4) $4 - 1\frac{3}{11} = 3\frac{11}{11} - 1\frac{3}{11} = 2\frac{8}{11}$
67. На сторонах квадрата записаны четыре натуральных числа. В каждой вершине квадрата записано число, равное произведению чисел, записанных на сторонах, для которых эта вершина является общей. Сумма чисел, записанных в вершинах, равна 55. Найдите сумму чисел, записанных на сторонах квадрата.
Решение:
Обозначим 4 натуральных числа буквами a, b, c, d.
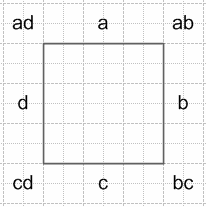
Пусть a, b, c, d - числа, написанные на сторонах квадрата. Тогда аd, ab, bc, cd - произведения этих чисел в углах квадрата, а сумма чисел, записанных в вершинах, равна 55.
Составим уравнение:
ad + ab + bc + cd = 55
(ad + ab) + (bc + cd) = 55
a(d + b) + c(b + d) = 55
(a + c)(b + d) = 55
Так как число 55 равно произведению только двух натуральных чисел (a + c) и (b + d), то этими числами могут быть только 5 и 11.
Значит, (a + c) + (b + d) = 5 + 11 = 16 − сумма чисел, записанных на сторонах квадрата.
Ответ: 16.