Ответы к странице 193

796. Для каждого значения a решите уравнение:
1) $\frac{x^2 - 8x + 7}{x - a} = 0$;
2) $\frac{x - a}{x^2 - 8x + 7} = 0$;
3) $\frac{x^2 - (3a + 2)x + 6a}{x - 6} = 0$;
4) $\frac{a(x - a)}{x + 3} = 0$.

Решение:

1) $\frac{x^2 - 8x + 7}{x - a} = 0$
x − a ≠ 0
x ≠ a
$x^2 - 8x + 7 = 0$
$D = b^2 - 4ac =(-8)^2 - 4 * 1 * 7 = 64 - 28 = 36 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{8 + \sqrt{36}}{2 * 1} = \frac{8 + 6}{2} = \frac{14}{2} = 7$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{8 - \sqrt{36}}{2 * 1} = \frac{8 - 6}{2} = \frac{2}{2} = 1$
$x^2 - 8x + 7 = (x - 7)(x - 1)$
$\frac{(x - 7)(x - 1)}{x - a} = 0$
если a = 1, то:
$\frac{(x - 7)(x - 1)}{x - 1} = 0$
x − 7 = 0
x = 7
если a = 7, то:
$\frac{(x - 7)(x - 1)}{x - 7} = 0$
x − 1 = 0
x = 1
если a ≠ 1 и a ≠ 7, то:
(x − 7)(x − 1) = 0
x − 7 = 0
x = 7
или
x − 1 = 0
x = 1
Ответ:
если a = 1: x = 7;
если a = 7: x = 2;
если a ≠ 1 и a ≠ 7: x = 1 и x = 7.

2) $\frac{x - a}{x^2 - 8x + 7} = 0$
$x^2 - 8x + 7 ≠ 0$
$D = b^2 - 4ac =(-8)^2 - 4 * 1 * 7 = 64 - 28 = 36 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{8 + \sqrt{36}}{2 * 1} = \frac{8 + 6}{2} = \frac{14}{2} ≠ 7$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{8 - \sqrt{36}}{2 * 1} = \frac{8 - 6}{2} = \frac{2}{2} ≠ 1$
$x^2 - 8x + 7 = (x - 7)(x - 1)$
$\frac{x - a}{(x - 7)(x - 1)} = 0$
если a = 1:
$\frac{x - 1}{(x - 7)(x - 1)} = 0$
$\frac{1}{x - 7} = 0$ − нет корней.
если a = 7:
$\frac{x - 7}{(x - 7)(x - 1)} = 0$
$\frac{1}{x - 1} = 0$ − нет корней.
если a ≠ 1 и a ≠ 7, то:
x − a = 0
x = a
Ответ:
если a = 1: нет корней;
если a = 7: нет корней;
если a ≠ 1 и a ≠ 7: x = a.

3) $\frac{x^2 - (3a + 2)x + 6a}{x - 6} = 0$
x − 6 ≠ 0
x ≠ 6
$x^2 - (3a + 2)x + 6a = 0$
$D = b^2 - 4ac =(-(3a + 2))^2 - 4 * 1 * 6a = 9a^2 + 12a + 4 - 24a = 9a^2 - 12a + 4 = (3a - 2)^2 ≥ 0$
а) если 3a − 2 ≠ 0, то:
3a ≠ 2
$a ≠ \frac{2}{3}$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{3a + 2 + \sqrt{(3a - 2)^2}}{2 * 1} = \frac{3a + 2 + 3a - 2}{2} = \frac{6a}{2} = 3a$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{3a + 2 - \sqrt{(3a - 2)^2}}{2 * 1} = \frac{3a + 2 - 3a + 2}{2} = \frac{4}{2} = 2$
$x^2 - (3a + 2)x + 6a = (x - 3a)(x - 2)$
$\frac{(x - 3a)(x - 2)}{x - 6} = 0$
если a = 2:
$\frac{(x - 3 * 2)(x - 2)}{x - 6} = 0$
$\frac{(x - 6)(x - 2)}{x - 6} = 0$
x − 2 = 0
x = 2
если a ≠ 2:
(x − 2)(x − 3a) = 0
x − 2 =0
x = 2
или
x − 3a = 0
x = 3a
б) если 3a − 2 = 0, то:
3a = 2
$a = \frac{2}{3}$, тогда:
$\frac{(x - 3 * \frac{2}{3})(x - 2)}{x - 6} = 0$
(x − 2)(x − 2) = 0
x − 2 = 0
x = 2
Ответ:
если a = 2 и $a = \frac{2}{3}$: x = 2;
если a ≠ 2 и $a ≠ \frac{2}{3}$: x = 3a или x = 2.

4) $\frac{a(x - a)}{x + 3} = 0$
x + 3 ≠ 0
x ≠ −3
еcли a = −3:
$\frac{-3(x - (-3))}{x + 3} = 0$
$\frac{-3(x + 3)}{x + 3} = 0$
−3 = 0 − нет корней.
если a = 0:
$\frac{0(x - 0)}{x + 3} = 0$
$\frac{0}{x + 3} = 0$
0 = 0
x − любое число, кроме 3.
еcли a ≠ −3:
a(x − a) = 0
a = 0
или
x − a = 0
x = a
еcли a ≠ 0 и a ≠ −3:
a(x − a) = 0
a = 0
или
x − a = 0
x = a
Ответ:
если a = −3: корней нет;
если a = 0: x ≠ 3;
если a ≠ 3: x = a;
еcли a ≠ 0 и a ≠ −3: x = a.

797. При каких значениях a уравнение $\frac{x^2 - ax + 5}{x - 1} = 0$ имеет единственный корень?

Решение:

$\frac{x^2 - ax + 5}{x - 1} = 0$
1)
$x^2 - ax + 5 = 0$
$D = b^2 - 4ac = (-a)^2 - 4 * 1 * 5 = a^2 - 20$
уравнение имеет единственный корень при D = 0, тогда:
$a^2 - 20 = 0$
$a^2 = 20$
$a_1 = \sqrt{20} = \sqrt{4 * 5} = 2\sqrt{5}$
$a_2 = -\sqrt{20} = -\sqrt{4 * 5} = -2\sqrt{5}$
2)
единственный корень имеет линейное уравнение, в этом случае один из линейных множителей числителя равен x − 1, тогда $x_1 = 1$:
$1^2 - a * 1 + 5 = 0$
1 − a + 5 = 0
−a = −5 − 1
−a = −6
a = 6
Ответ: при $a = 2\sqrt{5}$, $a = -2\sqrt{5}$ и a = 6 уравнение имеет единственный корень.

798. Верно ли утверждение, что при всех допустимых значениях переменной значение выражения
$(a - 1)^2(\frac{1}{a^2 - 1} + \frac{1}{a^2 - 2a + 1}) + \frac{2}{a + 1}$
является положительным числом?

Решение:

$(a - 1)^2(\frac{1}{a^2 - 1} + \frac{1}{a^2 - 2a + 1}) + \frac{2}{a + 1} = (a - 1)^2(\frac{1}{(a - 1)(a + 1)} + \frac{1}{(a - 1)^2}) + \frac{2}{a + 1} = (a - 1)^2 * \frac{a - 1 + a + 1}{(a - 1)^2(a + 1)} + \frac{2}{a + 1} = \frac{2a}{a + 1} + \frac{2}{a + 1} = \frac{2a + 2}{a + 1} = \frac{2(a + 1)}{a + 1} = 2 > 0$, значит при всех допустимых значениях переменной значение выражения является положительным числом.

799. Каким числом, рациональным или иррациональным, является значение выражения $\frac{\sqrt{6} + 2}{\sqrt{6} - 2} - \frac{\sqrt{6} - 2}{\sqrt{6} + 2}$?

Решение:

$\frac{\sqrt{6} + 2}{\sqrt{6} - 2} - \frac{\sqrt{6} - 2}{\sqrt{6} + 2} = \frac{(\sqrt{6} + 2)^2 - (\sqrt{6} - 2)^2}{(\sqrt{6} - 2)(\sqrt{6} + 2)} = \frac{6 + 4\sqrt{6} + 4 - (6 - 4\sqrt{6} + 4)}{6 - 4} = \frac{6 + 4\sqrt{6} + 4 - 6 + 4\sqrt{6} - 4)}{2} = \frac{8\sqrt{6}}{2} = 4\sqrt{6}$ − иррациональное число.

800. Постройте график функции:
$y = \begin{equation*} \begin{cases} -\frac{8}{x}, если\;x < -2 &\\ x^2, если\;x ≥ -2 & \end{cases} \end{equation*}$

Решение:

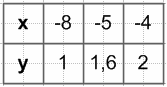
$y = -\frac{8}{x}$, если x < −2.

$y = x^2$, если x ≥ −2.

№801. На экране монитора компьютера записано число 1. Ежесекундно компьютер прибавляет к числу, находящемуся на экране, сумму его цифр. Может ли через некоторое время на экране появиться число 123456789?

Решение:

Обозначим S(n) сумму цифр натурального числа n. Поскольку числа n и S(n) имеют одинаковые остатки при делении на 3, то сумма n + S(n) кратна числу 3 в том и только в том случае, когда число n кратно числу 3. Сказанное означает, что на экране монитора не может появиться число, кратное 3, а число 123 456 789 кратно 3. На самом деле на экране монитора будут чередоваться числа, дающие при делении на 3 остаток 1, и числа, дающие при делении на 3 остаток 2.
Ответ: не может.