Ответы к странице 81
321. Задана функции $y = -\frac{36}{x}$. Найдите:
1) значение функции, если значение аргумента равно: −4; 0,9; 18;
2) значение аргумента, при котором значение функции равно: 6; −0,3; 8.
Решение:
1) $y = -\frac{36}{x}$
при x = −4:
$y = -\frac{36}{-4} = 9$
при x = 0,9:
$y = -\frac{36}{0,9} = -\frac{360}{9}= -40$
при x = 18:
$y = -\frac{36}{18} = -2$
2) $y = -\frac{36}{x}$
$x = -\frac{36}{y}$
при y = 6:
$x = -\frac{36}{6} = -6$
при y = −0,3:
$x = -\frac{36}{-0,3} = \frac{360}{3} = 120$
при y = 8:
$x = -\frac{36}{8} = -\frac{9}{2} = -4,5$
322. Постройте график функции $y = -\frac{8}{x}$. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно: 4; −1;
2) значение аргумента, при котором значение функции равно: 2; −8;
3) значения аргумента, при которых функция принимает положительные значения.
Решение:
1) $y = -\frac{8}{x}$
х -8 -4 -2 -1 1 2 4 8
у 1 2 4 8 -8 -4 -2 -1
при x = 4: y = −2;
при x = −1: y = 8.
2) при y = 2: x = −4;
при y = −8: x = 1.
3) при y > 0: x ∈ (−∞; 0).
323. Постройте график функции $y = \frac{10}{x}$. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно: 2; −10;
2) значение аргумента, при котором значение функции равно: 5; −2;
3) значение аргумента, при которых функция принимает отрицательные значения.
Решение:
1) х -10 -5 -2 -1 1 2 5 10
у -1 -2 -5 -10 10 5 2 1
при x = 2: y = 5;
при x = −10: y = −1.
2) при y = 5: x = 2;
при y = −2: x = −5.
3) при y < 0: x ∈ (−∞; 0).
324. Не выполняя построения графика функции $y = \frac{28}{x}$, определите, проходит ли график через точку:
1) A(−4;−7);
2) B(14;−2);
3) C(0,5;14);
4) D(0,2;140).
Решение:
1) $y = \frac{28}{x}$
A(−4;−7)
$-7 = \frac{28}{-4}$
−7 = −7
Ответ: график функции $y = \frac{28}{x}$ проходит через точку A(−4;−7)
2) $y = \frac{28}{x}$
B(14;−2)
$-2 = \frac{28}{14}$
−2 ≠ 2
Ответ: график функции $y = \frac{28}{x}$ не проходит через точку B(14;−2)
3) $y = \frac{28}{x}$
C(0,5;14)
$14 = \frac{28}{0,5}$
$14 = \frac{280}{5}$
14 ≠ 56
Ответ: график функции $y = \frac{28}{x}$ не проходит через точку C(0,5;14)
4) $y = \frac{28}{x}$
D(0,2;140)
$140 = \frac{28}{0,2}$
$140 = \frac{280}{2}$
140 = 140
Ответ: график функции $y = \frac{28}{x}$ проходит через точку D(0,2;140)
325. Истинным или ложным является высказывание: график функции $y = -\frac{48}{x}$ проходит через точку:
1) A(−6;−8);
2) B(12;−4);
3) C(0,3;−16);
4) D(0,4;−120)?
Решение:
1) $y = -\frac{48}{x}$
A(−6;−8)
$-8 = -\frac{48}{-6}$
−8 ≠ 8
Ответ: график функции $y = -\frac{48}{x}$ не проходит через точку A(−6;−8)
2) $y = -\frac{48}{x}$
B(12;−4)
$-4 = -\frac{48}{12}$
−4 = −4
Ответ: график функции $y = -\frac{48}{x}$ проходит через точку B(12;−4)
3) $y = -\frac{48}{x}$
C(0,3;−16)
$-16 = -\frac{48}{0,3}$
$-16 = -\frac{480}{3}$
−16 ≠ −160
Ответ: график функции $y = -\frac{48}{x}$ не проходит через точку C(0,3;−16)
4) $y = -\frac{48}{x}$
D(0,4;−120)
$-120 = -\frac{48}{0,4}$
$-120 = -\frac{480}{4}$
−120 = −120
Ответ: график функции $y = -\frac{48}{x}$ проходит через точку D(0,4;−120)
326. На рисунке 8 изображен график зависимости времени t движения из пункта A в пункт B от скорости v движения. Пользуясь графиком, определите:
1) за какое время можно добраться из пункта A в пункт B, если двигаться со скоростью 8 км/ч; 24 км/ч;
2) с какой скоростью нужно двигаться, чтобы добраться из пункта A в пункт B за 3 ч; за 4 ч;
3) чему равно расстояние между пунктами A и B.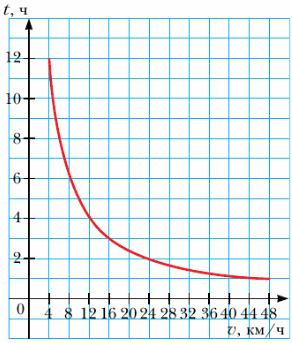
Решение:
1) Если двигаться со скоростью 8 км/ч, то из пункта A в пункт B можно добраться за 6 часов.
Если двигаться со скоростью 24 км/ч, то из пункта A в пункт B можно добраться за 2 часа.
2) Чтобы добраться из пункта A в пункт B за 3 ч, нужно двигаться со скоростью 16 км/ч.
Чтобы добраться из пункта A в пункт B за 4 ч, нужно двигаться со скоростью 12 км/ч.
3) Чтобы добраться из пункта A в пункт B за 4 ч, нужно двигаться со скоростью 12 км/ч, тогда:
4 * 12 = 48 (км) − расстояние между пунктами A и B.