Ответы к странице 92

352. Не выполняя построения, найдите координаты точек пересечения графиков функций $y = x^2$ и y = 4x − 4. Постройте графики данных функций и отметьте найденные точки.

Решение:

$\begin{equation*} \begin{cases} y = x^2 &\\ y = 4x - 4 & \end{cases} \end{equation*}$
$y - y = x^2 - (4x - 4)$
$x^2 - 4x + 4 = 0$
$(x - 2)^2 = 0$
x − 2 = 0
x = 2
y = 4x − 4 = 4 * 2 − 4 = 8 − 4 = 4
Точка пересечения графиков функций $y = x^2$ и y = 4x − 4 имеет координаты (2;4)
$y = x^2$

y = 4x − 4

353. Решите графически уравнение:
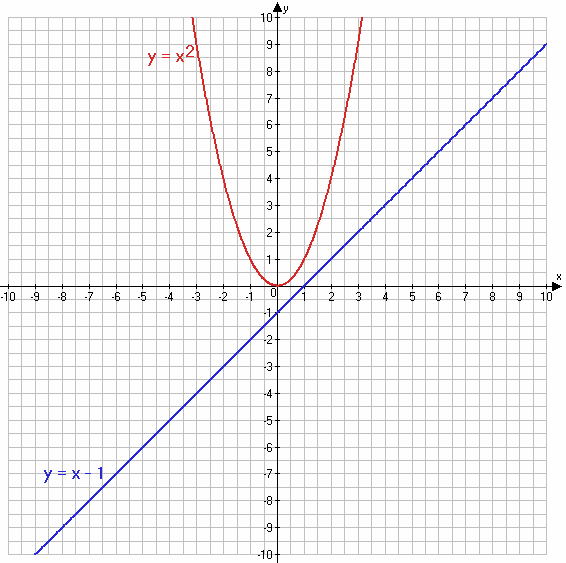
1) $x^2 = x - 1$;
2) $x^2 - 2x - 3 = 0$;
3) $x^2 = \frac{8}{x}$.

Решение:

1) $x^2 = x - 1$
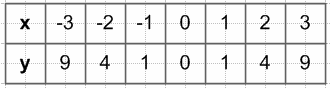
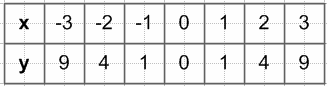
$y = x^2$

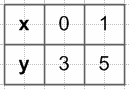
y = x − 1


Ответ: нет корней

2) $x^2 - 2x - 3 = 0$
$x^2 = 2x + 3$

$y = x^2$

y = 2x + 3


Ответ: x = −1 и x = 3

3) $x^2 = \frac{8}{x}$

$y = x^2$

$y = \frac{8}{x}$


Ответ: x = 2

354. Решите графически уравнение:
1) $x^2 = -4x - 3$;
2) $x^2 - 3x + 5 = 0$;
3) $x^2 + \frac{1}{x} = 0$.

Решение:

1) $x^2 = -4x - 3$

$y = x^2$

y = −4x − 3


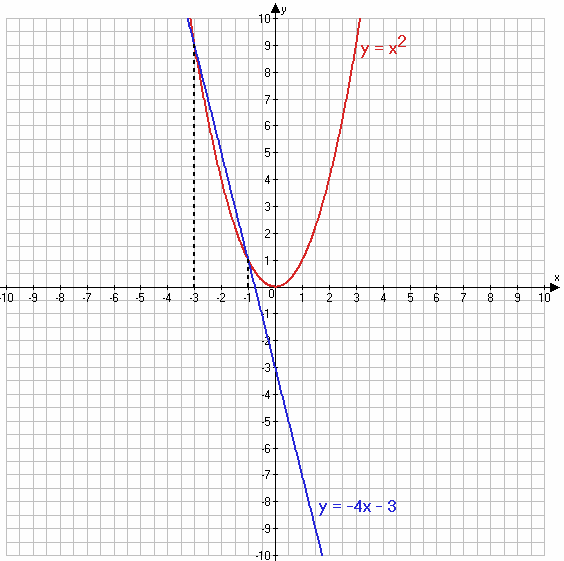
Ответ: x = −3 и x = −1

2) $x^2 - 3x + 5 = 0$
$x^2 = 3x - 5$

$y = x^2$

y = 3x − 5


Ответ: нет корней

3) $x^2 + \frac{1}{x} = 0$
$x^2 = -\frac{1}{x}$

$y = x^2$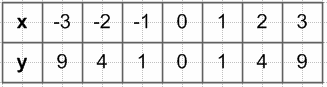

$y = -\frac{1}{x}$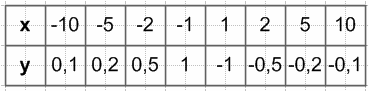


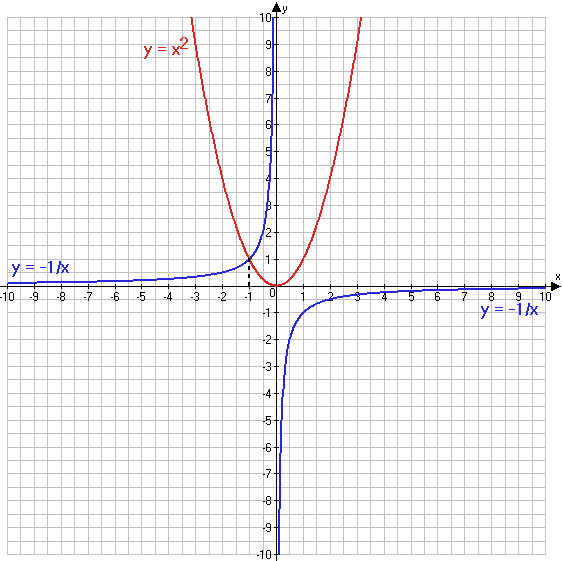
Ответ: x = −1

355. Определите графически количество решений системы уравнений:
1)
$\begin{equation*} \begin{cases} y = x^2 &\\ y = 2 & \end{cases} \end{equation*}$
2)
$\begin{equation*} \begin{cases} y = x^2 &\\ y = -2 & \end{cases} \end{equation*}$
3)
$\begin{equation*} \begin{cases} y - x^2 = 0 &\\ x - y + 6 = 0 & \end{cases} \end{equation*}$
4)
$\begin{equation*} \begin{cases} y - x^2 = 0 &\\ 2x + 5y = 10 & \end{cases} \end{equation*}$

Решение:

1) $\begin{equation*} \begin{cases} y = x^2 &\\ y = 2 & \end{cases} \end{equation*}$

$y = x^2$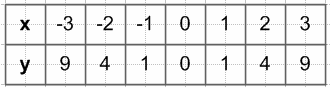


Ответ: система уравнений имеет 2 решения

2) $\begin{equation*} \begin{cases} y = x^2 &\\ y = -2 & \end{cases} \end{equation*}$

$y = x^2$


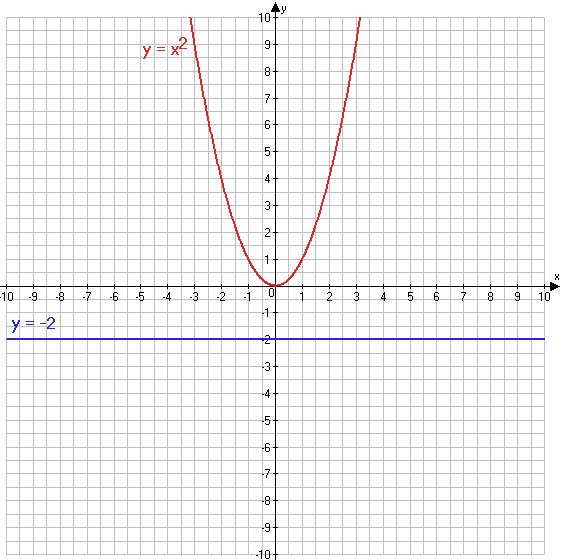
Ответ: система уравнений не имеет решений

3) $\begin{equation*} \begin{cases} y - x^2 = 0 &\\ x - y + 6 = 0 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x^2 &\\ y = x + 6 & \end{cases} \end{equation*}$

$y = x^2$

y = x + 6


Ответ: система уравнений имеет 2 решения

4) $\begin{equation*} \begin{cases} y - x^2 = 0 &\\ 2x + 5y = 10 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x^2 &\\ 5y = 10 - 2x & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x^2 &\\ y = 2 - \frac{2}{5}x & \end{cases} \end{equation*}$

$y = x^2$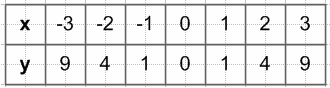

$y = 2 - \frac{2}{5}x$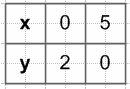


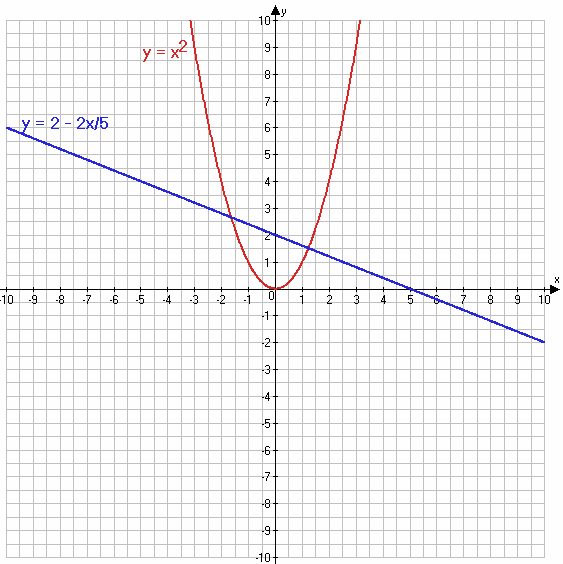
Ответ: система уравнений имеет 2 решения

356. Определите графически количество решений системы уравнений:
1)
$\begin{equation*} \begin{cases} y = x^2 &\\ 3x + 2y = -6 & \end{cases} \end{equation*}$
2)
$\begin{equation*} \begin{cases} y = x^2 &\\ x - 3y = -3 & \end{cases} \end{equation*}$

Решение:

1) $\begin{equation*} \begin{cases} y = x^2 &\\ 3x + 2y = -6 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x^2 &\\ 2y = -6 - 3x & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x^2 &\\ y = -3 - \frac{3}{2}x & \end{cases} \end{equation*}$
$y = x^2$

$y = -3 - \frac{3}{2}x$


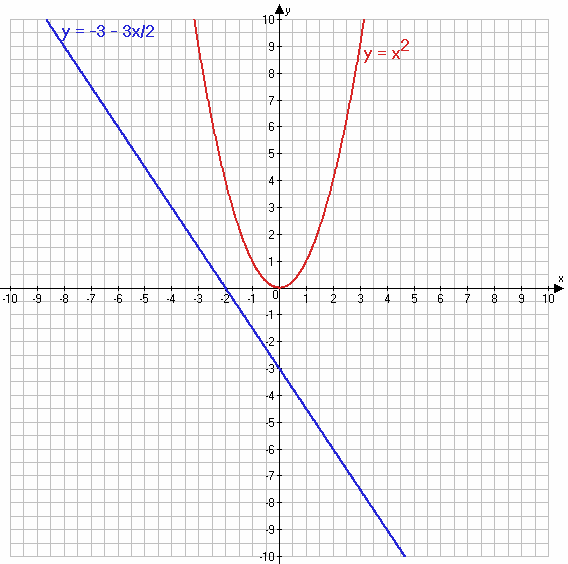
Ответ: система уравнения не имеет решений

2) $\begin{equation*} \begin{cases} y = x^2 &\\ x - 3y = -3 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x^2 &\\ 3y = x + 3 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x^2 &\\ y = \frac{1}{3}x + 1 & \end{cases} \end{equation*}$

$y = x^2$

$y = \frac{1}{3}x + 1$


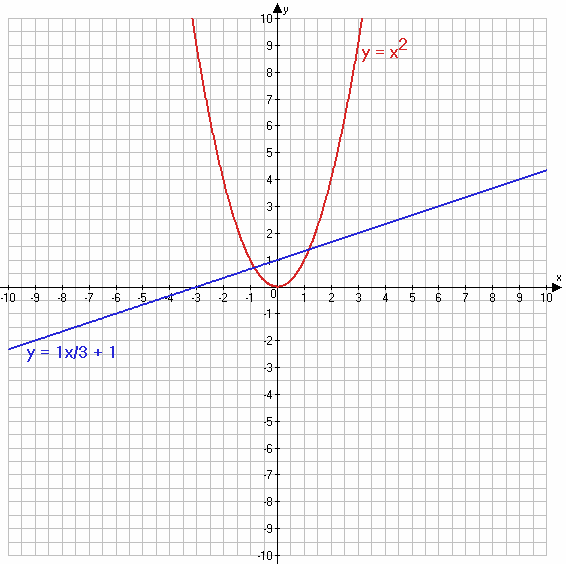
Ответ: система уравнений имеет 2 решения

357. Функция ƒ задана следующим способом:
$f(x) = \begin{equation*} \begin{cases} 4, если\;x ≤ -2&\\ x^2, если\;-2 < x < 1&\\ 2x - 1, если\;x ≥ 1 & \end{cases} \end{equation*}$
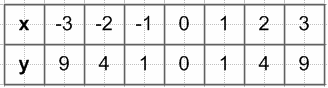
1) Найдите ƒ(−3), ƒ(−2), ƒ(−1), ƒ(1), ƒ(3), ƒ(0,5).
2) Постройте график данной функции.

Решение:

1) ƒ(−3) = 4
ƒ(−2) = 4
$ƒ(-1) = (-1)^2 = 1$
ƒ(1) = 2 * 1 − 1 = 2 − 1 = 1
ƒ(3) = 2 * 3 − 1 = 6 − 1 = 5
$ƒ(0,5) = (0,5)^2 = 0,25$

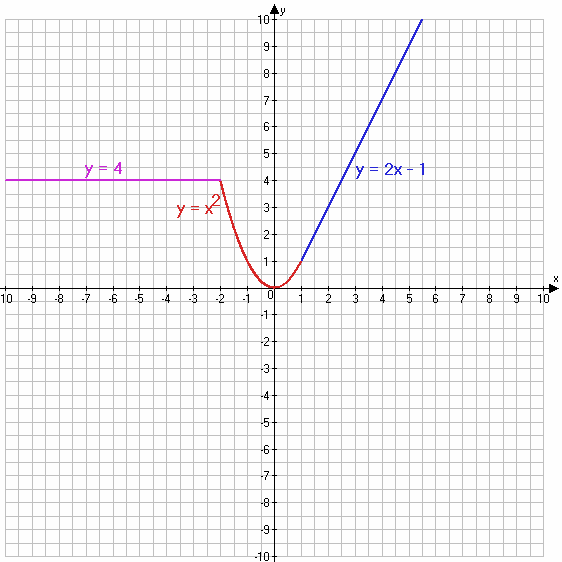
2) y = 4, если x ≤ −2 − прямая

$y = x^2$, если −2 < x < 1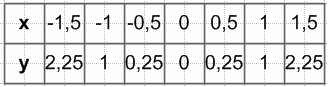

y = 2x − 1, если x ≥ 1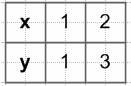

358. Дана функция
$f(x) = \begin{equation*} \begin{cases} 2x + 3, если\;x ≤ -1&\\ x^2, если\;-1 < x < 2&\\ 4, если\;x ≥ 2 & \end{cases} \end{equation*}$
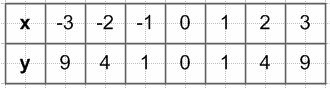
1) Найдите ƒ(−4), ƒ(−0,3), ƒ(1,9), ƒ(3), ƒ(−1), ƒ(2).
2) Постройте график данной функции.

Решение:

1) ƒ(−4) = 2 * (−4) + 3 = −8 + 3 = −5
$ƒ(-0,3) = (-0,3)^2 = 0,09$
$ƒ(1,9) = 1,9^2 = 3,61$
ƒ(3) = 4
ƒ(−1) = 2 * (−1) + 3 = −2 + 3 = 1
ƒ(2) = 4

2) y = 2x + 3, если x ≤ −1

$y = x^2$, если −1 < x < 2

y = 4, если x ≥ 2 − прямая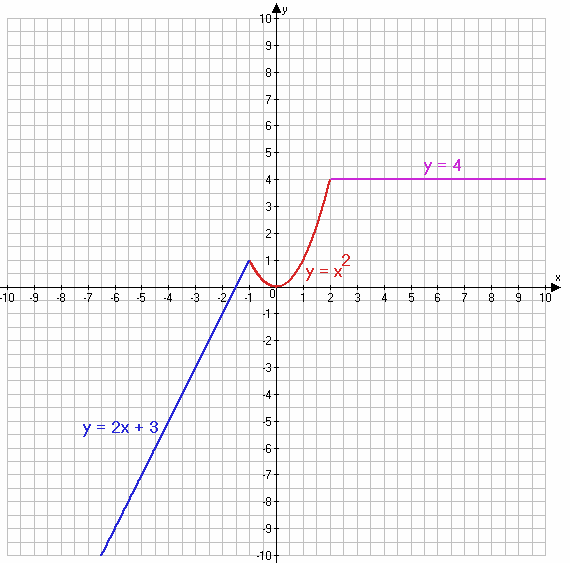

359. Дана функция
$f(x) = \begin{equation*} \begin{cases} x^2, если\;x ≤ 0 &\\ x + 1, если\; x > 0 & \end{cases} \end{equation*}$
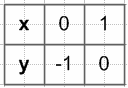
1) Найдите ƒ(−7), ƒ(0), ƒ(2).
2) Постройте график данной функции.

Решение:

1) $ƒ(-7) = (-7)^2 = 49$
$ƒ(0) = 0^2 = 0$
ƒ(2) = 2 + 1 = 3

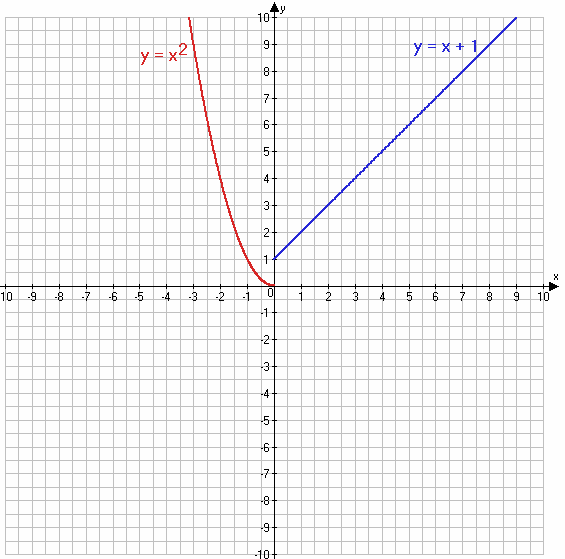
2) $y = x^2$, если x ≤ 0

y = x + 1, если x > 0

360. Дана функция
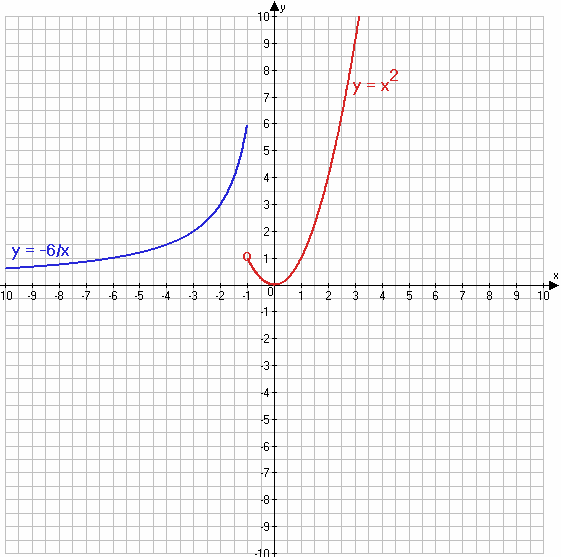
$f(x) = \begin{equation*} \begin{cases} -\frac{6}{x}, если\;x ≤ -1 &\\ x^2, если\; x > -1 & \end{cases} \end{equation*}$
1) Найдите ƒ(−12), ƒ(−1), ƒ(−0,9), ƒ(3), ƒ(0).
2) Постройте график данной функции.

Решение:

1) $ƒ(-12) = -\frac{6}{-12} = \frac{1}{2}$
$ƒ(-1) = -\frac{6}{-1} = 6$
$ƒ(-0,9) = (-0,9)^2 = 0,81$
$ƒ(3) = 3^2 = 9$
$ƒ(0) = 0^2 = 0$

2) $y = -\frac{6}{x}$, если x ≤ −1

$y = x^2$, если x > −1