Ответы к странице 203

833. Найдите значение выражения $a^2 - 2\sqrt{5}a + 2$ при $a = \sqrt{5} - 3$.

Решение:

$a^2 - 2\sqrt{5}a + 2$
при $a = \sqrt{5} - 3$:
$(\sqrt{5} - 3)^2 - 2\sqrt{5} * (\sqrt{5} - 3) + 2 = (\sqrt{5})^2 - 2 * 3\sqrt{5} + 3^2 - 2 * 5 + 6\sqrt{5} + 2 = 5 - 6\sqrt{5} + 9 - 10 + 6\sqrt{5} + 2 = 6$

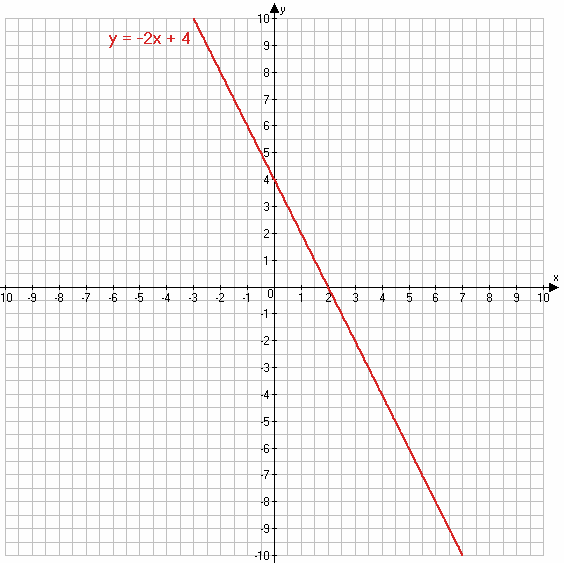
834. Постройте график функции y = −2x + 4.
1) Чему равен нуль данной функции?
2) Укажите значения x, при которых y > 0.
3) Проходит ли график функции через точку M (−36; 68)?

Решение:

y = −2x + 4
х 0 1
у 4 2

1)
−2x + 4 = 0
−2x = −4
x = 2 − нуль функции.
2)
y > 0 при x < 2
3)
M (−36; 68)
68 = −2 * (−36) + 4
68 = 72 + 4
68 ≠ 76
график функции не проходит через точку M (−36; 68)

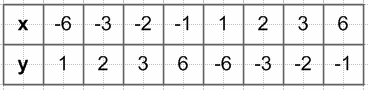
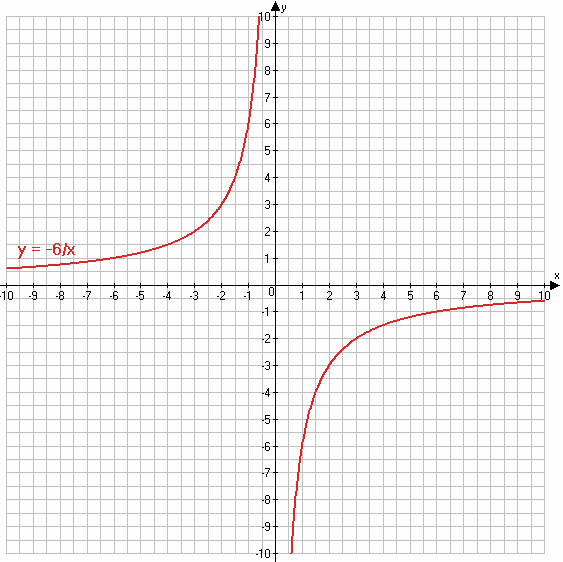
835. При каком значении k график функции $y = \frac{k}{x}$ проходит через точку $A(-\sqrt{12}; \sqrt{3})$? Постройте этот график.

Решение:

$y = \frac{k}{x}$
$A(-\sqrt{12}; \sqrt{3})$
$\sqrt{3} = \frac{k}{-\sqrt{12}}$
$k = \sqrt{3} * (-\sqrt{12})$
$k = -\sqrt{36}$
k = −6
при k = −6 график функции проходит через данную точку.
$y = -\frac{6}{x}$

836. Какое из равенств верно:
$\sqrt{(\sqrt{3} - 2)^2} = \sqrt{3} - 2$ или $\sqrt{(\sqrt{3} - 2)^2} = 2 - \sqrt{3}$?
Ответ обоснуйте.

Решение:

$\sqrt{(\sqrt{3} - 2)^2} = |\sqrt{3} - 2| = -(\sqrt{3} - 2) = 2 - \sqrt{3}$, так как:
$2 = \sqrt{2^2}$
$2 = \sqrt{4}$
$\sqrt{3} < \sqrt{4}$
$\sqrt{3} < 2$
Ответ: $\sqrt{(\sqrt{3} - 2)^2} = 2 - \sqrt{3}$, так как $\sqrt{3} < 2$.

837. Упростите выражение:
1) $(\frac{1}{4}a^{-1}b^{-3})^{-2}$;
2) $(\frac{a^4}{b^{-5}})^{-3}$;
3) $(0,2a^{-1}b^2)^2 * 4a^5b^{-4}$.

Решение:

1) $(\frac{1}{4}a^{-1}b^{-3})^{-2} = (\frac{1}{4})^{-2} * (a^{-1})^{-2} * (b^{-3})^{-2} = 4^2 * a^2 * b^6 = 16a^2b^6$

2) $(\frac{a^4}{b^{-5}})^{-3} = \frac{(a^4)^{-3}}{(b^{-5})^{-3}} = \frac{a^{-12}}{b^{15}} = \frac{1}{a^{12}b^{15}}$

3) $(0,2a^{-1}b^2)^2 * 4a^5b^{-4} = 0,2^2 * (a^{-1})^2 * (b^2)^2 * 4a^5b^{-4} = 0,04a^{-2}b^4 * 4a^5b^{-4} = 0,16a^3b^0 = 0,16a^3$

№838. На тарелке лежит 9 кусочков сыра разной массы. Докажите, что можно один из кусочков сыра разрезать на две части так, что полученные 10 кусочков можно будет разложить на две тарелки и при этом масса сыра на каждой из них будет одинаковой.

Решение:

Упорядочим кусочки по возрастанию массы: m₁ m₂ ... m₉.
На одну тарелку положим кусочки с массами m₁, m₃, m₅, m₇, а на другую − с массами m₂, m₄, m₆, m₈.
Тогда m₁ + m₃ + m₅ + m₇  <  m₂ + m₄ + m₆ + m₈.
Поскольку m₃ + m₅ + m₇ + m₉ > m₂ + m₄ + m₆ + m₈, то тем более
m₁ + m₃ + m₅ + m₇ + m₉  >  m₂ + m₄ + m₆ + m₈.
Тогда понятно, что m₉ = (m₂ + m₄ + m₆ + m₈) − (m₁ + m₃ + m₅ + m₇).
Следовательно, если обозначить d = (m₂ + m₄ + m₆ + m₈) −  (m₁ + m₃ + m₅ + m₇), то кусочек с массой, равной m₉, можно разрезать на две части, удовлетворяющие условию, таким образом: 
m₉ + d  и  m₉-d
    2               2