Ответы к странице 148

586. Сравните числа:
1) $\sqrt{\frac{1}{3}}$ и $\sqrt{\frac{1}{5}}$;
2) 9 и $\sqrt{82}$;
3) $\sqrt{33}$ и 6;
4) $3\sqrt{5}$ и $\sqrt{42}$;
5) $\sqrt{30}$ и $2\sqrt{7}$;
6) $7\sqrt{\frac{1}{7}}$ и $\frac{1}{2}\sqrt{20}$.

Решение:

1) $\frac{1}{3} > \frac{1}{5}$, значит:
$\sqrt{\frac{1}{3}} > \sqrt{\frac{1}{5}}$

2) $9 = \sqrt{81}$
$\sqrt{81} < \sqrt{82}$, значит:
$9 < \sqrt{82}$

3) $6 = \sqrt{36}$
$\sqrt{33} < \sqrt{36}$, значит:
$\sqrt{33} < 6$

4) $3\sqrt{5} = \sqrt{9 * 5} = \sqrt{45}$
$\sqrt{45} > \sqrt{42}$, значит:
$3\sqrt{5} > \sqrt{42}$

5) $2\sqrt{7} = \sqrt{4 * 7} = \sqrt{28}$
$\sqrt{30} > \sqrt{28}$, значит:
$\sqrt{30} > 2\sqrt{7}$

6) $7\sqrt{\frac{1}{7}} = \sqrt{49 * \frac{1}{7}} = \sqrt{7}$
$\sqrt{\frac{1}{4} * 20} = \sqrt{5}$
$\sqrt{7} > \sqrt{5}$, значит:
$7\sqrt{\frac{1}{7}} > \frac{1}{2}\sqrt{20}$

587. Не выполняя построения, найдите координаты точки пересечения графика функции $y = \sqrt{x}$ и прямой:
1) y = 1;
2) y = 0,8;
3) y = −6;
4) y = 500.

Решение:

1) $y = \sqrt{x}$
y = 1
$1 = \sqrt{x}$
$(\sqrt{x})^2 = 1^2$
x = 1
Ответ: точка пересечения графика функции $y = \sqrt{x}$ и прямой имеет координаты (1; 1)

2) $y = \sqrt{x}$
y = 0,8
$0,8 = \sqrt{x}$
$(\sqrt{x})^2 = 0,8^2$
x = 0,64
Ответ: точка пересечения графика функции $y = \sqrt{x}$ и прямой имеет координаты (0,64; 0,8)

3) $y = \sqrt{x}$
y = −6
$-6 = \sqrt{x}$
нет решений
Ответ: график функции $y = \sqrt{x}$ и прямая не имеет точек пересечения

4) $y = \sqrt{x}$
y = 500
$500 = \sqrt{x}$
$(\sqrt{x})^2 = 500^2$
x = 250000
Ответ: точка пересечения графика функции $y = \sqrt{x}$ и прямой имеет координаты (250000; 500)

588. Запишите в порядке убывания числа:
$8; \sqrt{62}; 7,9; \sqrt{65}; 8,2$.

Решение:

$8 = \sqrt{64}$
$7,9 = \sqrt{62,41}$
$8,2 = \sqrt{67,24}$
67,24 > 65 > 64 > 62,41 > 62, значит:
$8,2 > \sqrt{65} > 8 > 7,9 > \sqrt{62}$

589. Запишите в порядке возрастания числа:
$\sqrt{38}; 6,1; 6; \sqrt{35}; 5,9$.

Решение:

$6,1 = \sqrt{6,1^2} = \sqrt{37,21}$
$6 = \sqrt{6^2} = \sqrt{36}$
$5,9 = \sqrt{5,9^2} = \sqrt{34,81}$
34,81 < 35 < 36 < 37,21 < 38, значит:
$5,9 < \sqrt{35} < 6 < 6,1 < \sqrt{38}$

590. Между какими двумя последовательными целыми числами находится на координатной прямой число:
1) $\sqrt{2}$;
2) $\sqrt{3}$;
3) $\sqrt{5}$;
4) $\sqrt{7}$;
5) $\sqrt{13}$;
6) $\sqrt{0,98}$;
7) $\sqrt{59}$;
8) $-\sqrt{115}$;
9) $-\sqrt{76,19}$?

Решение:

1) $\sqrt{1} < \sqrt{2} < \sqrt{4}$
$1 < \sqrt{2} < 2$
Ответ: между числами 1 и 2

2) $\sqrt{1} < \sqrt{3} < \sqrt{4}$
$1 < \sqrt{3} < 2$
Ответ: между числами 1 и 2

3) $\sqrt{4} < \sqrt{5} < \sqrt{9}$
$2 < \sqrt{3} < 3$
Ответ: между числами 2 и 3

4) $\sqrt{4} < \sqrt{7} < \sqrt{9}$
$2 < \sqrt{7} < 3$
Ответ: между числами 2 и 3

5) $\sqrt{9} < \sqrt{13} < \sqrt{16}$
$3 < \sqrt{13} < 4$
Ответ: между числами 3 и 4

6) $\sqrt{0} < \sqrt{0,98} < \sqrt{1}$
$0 < \sqrt{0,98} < 1$
Ответ: между числами 0 и 1

7) $\sqrt{49} < \sqrt{59} < \sqrt{64}$
$7 < \sqrt{59} < 8$
Ответ: между числами 7 и 8

8) $-\sqrt{121} < -\sqrt{115} < -\sqrt{100}$
$-11 < -\sqrt{115} < -10$
Ответ: между числами −11 и −10

9) $-\sqrt{81} < -\sqrt{76,19} < -\sqrt{64}$
$-9 < -\sqrt{76,19} < -8$
Ответ: между числами −9 и −8

591. Между какими двумя последовательными целыми числами находится на координатной прямой число:
1) $\sqrt{6}$;
2) $\sqrt{19}$;
3) $\sqrt{29}$;
4) $\sqrt{160}$;
5) $-\sqrt{86}$;
6) $-\sqrt{30,5}$?

Решение:

1) $\sqrt{4} < \sqrt{6} < \sqrt{9}$
$2 < \sqrt{2} < 3$
Ответ: между числами 2 и 3

2) $\sqrt{16} < \sqrt{19} < \sqrt{25}$
$4 < \sqrt{19} < 5$
Ответ: между числами 4 и 5

3) $\sqrt{25} < \sqrt{29} < \sqrt{36}$
$5 < \sqrt{29} < 6$
Ответ: между числами 5 и 6

4) $\sqrt{160}$
$\sqrt{144} < \sqrt{160} < \sqrt{169}$
$12 < \sqrt{160} < 13$
Ответ: между числами 12 и 13

5) $-\sqrt{100} < -\sqrt{86} < -\sqrt{81}$
$-10 < -\sqrt{86} < -9$
Ответ: между числами −10 и −9

6) $-\sqrt{30,5}$
$-\sqrt{36} < -\sqrt{30,5} < -\sqrt{25}$
$-6 < -\sqrt{30,5} < -5$
Ответ: между числами −6 и −5

592. Укажите все целые числа, расположенные на координатной прямой между числами:
1) 3 и $\sqrt{68}$;
2) $\sqrt{7}$ и $\sqrt{77}$;
3) $-\sqrt{31}$ и −2,3;
4) $-\sqrt{42}$ и 2,8.

Решение:

1) $\sqrt{68} < \sqrt{81}$
$\sqrt{68} < 9$
3 < x < 9
Ответ: 4, 5, 6, 7, 8.

2) $\sqrt{4} < \sqrt{7}$
$2 < \sqrt{7}$
$\sqrt{77} < \sqrt{81}$
$\sqrt{77} < 9$
2 < x < 9
Ответ: 3, 4, 5, 6, 7, 8.

3) $-\sqrt{31}$ и −2,3
$-\sqrt{31} < -\sqrt{36}$
$-\sqrt{31} < -6$
−6 < x < −2,3
Ответ: −5, −4, −3.

4) $-\sqrt{42}$ и 2,8
$-\sqrt{49} < -\sqrt{42}$
$-7 < -\sqrt{42}$
−7 < x < 2,8
Ответ: −6, −5, −4, −3, −2, −1, 0, 1, 2.

593. Укажите все целые числа, расположенные на координатной прямой между числами:
1) $\sqrt{3}$ и $\sqrt{13}$;
2) $\sqrt{10}$ и $\sqrt{90}$;
3) $-\sqrt{145}$ и $-\sqrt{47}$.

Решение:

1) $\sqrt{1} < \sqrt{3}$
$1 < \sqrt{3}$
$\sqrt{13} < \sqrt{16}$
$\sqrt{13} < 4$
1 < x < 4
Ответ: 2, 3.

2) $\sqrt{9} < \sqrt{10}$
$3 < \sqrt{10}$
$\sqrt{90} < \sqrt{100}$
$\sqrt{90} < 10$
3 < x < 10
Ответ: 4, 5, 6, 7, 8, 9.

3) $-\sqrt{169} < -\sqrt{145}$
$-13 < -\sqrt{145}$
$-\sqrt{47} < -\sqrt{36}$
$-\sqrt{47} < -6$
−13 < x < −6
Ответ: −12, −11, −10, −9, −8, −7.

594. При каких значениях x выполняется неравенство:
1) $\sqrt{x} ≥ 2$;
2) $\sqrt{x} < 4$;
3) $6 ≤ \sqrt{x} < 9$?

Решение:

1) $\sqrt{x} ≥ 2$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x ≥ 2^2 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x ≥ 4 & \end{cases} \end{equation*}$
Ответ: неравенство выполняется при x ≥ 4

2) $\sqrt{x} < 4$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x < 4^2 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x < 16 & \end{cases} \end{equation*}$
Ответ: неравенство выполняется при 0 ≤ x < 16

3) $6 ≤ \sqrt{x} < 9$
$\begin{equation*} \begin{cases} x ≥ 6^2 &\\ x < 9^2 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 36 &\\ x < 81 & \end{cases} \end{equation*}$
Ответ: неравенство выполняется при 36 ≤ x < 81

595. При каких значениях x выполняется неравенство:
1) $\sqrt{x} ≤ 8$;
2) $\sqrt{x} > 7$;
3) $10 ≤ \sqrt{x} ≤ 20$?

Решение:

1) $\sqrt{x} ≤ 8$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x ≤ 8^2 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x ≤ 64 & \end{cases} \end{equation*}$
Ответ: неравенство выполняется при 0 ≤ x ≤ 64

2) $\sqrt{x} > 7$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x > 7^2 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x > 49 & \end{cases} \end{equation*}$
Ответ: неравенство выполняется при x > 49

3) $10 ≤ \sqrt{x} ≤ 20$
$\begin{equation*} \begin{cases} x ≥ 10^2 &\\ x ≤ 20^2& \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 100 &\\ x ≤ 400 & \end{cases} \end{equation*}$
Ответ: неравенство выполняется при 100 ≤ x ≤ 400

596. Решите графически уравнение:
1) $\sqrt{x} = x$;
2) $\sqrt{x} = x^2$;
3) $\sqrt{x} = x + 2$;
4) $\sqrt{x} = 0,5x + 0,5$;
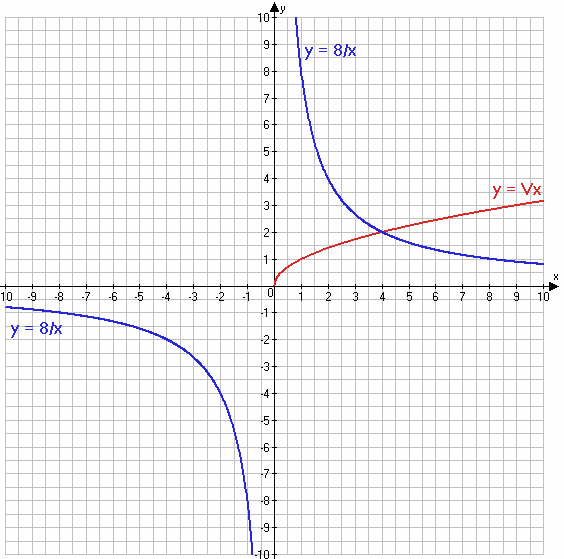
5) $\sqrt{x} = \frac{8}{x}$;
6) $\sqrt{x} = 1,5 - 0,5x$.

Решение:

1) $\sqrt{x} = x$
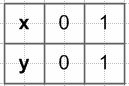
$y = \sqrt{x}$

y = x


Ответ: x = 0 и x = 1

2) $\sqrt{x} = x^2$
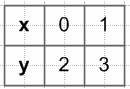
$y = \sqrt{x}$

$y = x^2$


Ответ: x = 0 и x = 1

3) $\sqrt{x} = x + 2$
$\sqrt{x} = x$

$y = x + 2$


Ответ: нет корней

4) $\sqrt{x} = 0,5x + 0,5$
$\sqrt{x} = x$

y = 0,5x + 0,5


Ответ: x = 1

5) $\sqrt{x} = \frac{8}{x}$
$\sqrt{x} = x$

$y = \frac{8}{x}$


Ответ: x = 4

6) $\sqrt{x} = 1,5 - 0,5x$
$\sqrt{x} = x$

y = 1,5 − 0,5x


Ответ: x = 1

597. Решите графически уравнение:
1) $\sqrt{x} = -x - 1$;
2) $\sqrt{x} = 2 - x$;
3) $\sqrt{x} = \frac{1}{x}$.

Решение:

1) $\sqrt{x} = -x - 1$
$y = \sqrt{x}$

y = −x − 1


Ответ: нет корней

2) $\sqrt{x} = 2 - x$
$y = \sqrt{x}$

y = 2 − x


Ответ: x = 1

3) $\sqrt{x} = \frac{1}{x}$
$y = \sqrt{x}$

$y = \frac{1}{x}$


Ответ: x = 1