Ответы к странице 33-34
Задание №1 "Проверьте себя" в тестовой форме
1. Какое из данных выражений является целым?
А) $\frac{m + n}{m}$
Б) $\frac{m + n}{7}$
В) $\frac{m + n}{7m}$
Г) $m + \frac{n}{7m}$
Решение:
Ответ: Б) $\frac{m + n}{7}$ − целое выражение
2. При каком значении переменной не имеет смысла выражение $\frac{3a}{2a - 10}$?
А) 0
Б) 10
В) 5
Г) 0; 5
Решение:
$\frac{3a}{2a - 10}$
2a − 10 ≠ 0
2a ≠ 10
a ≠ 5
Ответ: В) 5
3. При каких значениях аргумента функция $y = \frac{x + 2}{x^2 - 1}$ не определена?
А) −1; 1
Б) 1
В) −2; −1; 1
Г) −2; 1
Решение:
$y = \frac{x + 2}{x^2 - 1}$
$x^2 - 1 ≠ 0$
$x^2 ≠ 1$
x ≠ ±1
Ответ: А) −1; 1.
4. Сократите дробь $\frac{21a^6}{14a^3}$.
А) $\frac{3a^3}{2}$
Б) $\frac{3a^2}{2}$
В) $\frac{3}{2a^3}$
Г) $\frac{3}{2a^2}$
Решение:
$\frac{21a^6}{14a^3} = \frac{7a^3 * 3a^3}{7a^3 * 2} = \frac{3a^3}{2}$
Ответ: А) $\frac{3a^3}{2}$
5. Какой из данных дробей тождественно равна дробь $\frac{5b - 15}{b^2 - 9}$?
А) $\frac{b - 3}{5}$
Б) $\frac{b + 3}{5}$
В) $\frac{5}{b - 3}$
Г) $\frac{5}{b + 3}$
Решение:
$\frac{5b - 15}{b^2 - 9} = \frac{5(b - 3)}{(b - 3)(b + 3)} = \frac{5}{b + 3}$
Ответ: Г) $\frac{5}{b + 3}$
6. Сократите дробь $\frac{12c^2 - 4c}{3c - 1}$.
А) 4c
Б) −4c
В) $\frac{1}{4c}$
Г) $-\frac{1}{4c}$
Решение:
$\frac{12c^2 - 4c}{3c - 1} = \frac{4c(3c - 1)}{3c - 1} = 4c$
Ответ: А) 4c
7. Выполните вычитание:
$\frac{5x}{x - 2} - \frac{10}{x - 2}$.
А) $\frac{x + 2}{x - 2}$
Б) $\frac{5x + 10}{x - 2}$
В) 5
Г) −5
Решение:
$\frac{5x}{x - 2} - \frac{10}{x - 2} = \frac{5x - 10}{x - 2} = \frac{5(x - 2)}{x - 2} = 5$
Ответ: В) 5
8. Выполните сложение:
$\frac{4 - m}{m - 3} + \frac{2m - 5}{3 - m}$.
А) $\frac{m - 1}{m - 3}$
Б) $\frac{1 - 3m}{m - 3}$
В) 3
Г) −3
Решение:
$\frac{4 - m}{m - 3} + \frac{2m - 5}{3 - m} = \frac{4 - m}{m - 3} - \frac{2m - 5}{m - 3} = \frac{4 - m - (2m - 5)}{m - 3} = \frac{4 - m - 2m + 5}{m - 3} = \frac{-3m + 9}{m - 3} = \frac{-3(m - 3)}{m - 3} = -3$
Ответ: Г) −3
9. Представьте в виде дроби выражение $\frac{3n^2}{n - 6} - 3n$.
А) $\frac{3n}{n - 4}$
Б) $\frac{3n}{4 - n}$
В) $\frac{18n}{n - 6}$
Г) $\frac{18}{6 - n}$
Решение:
$\frac{3n^2}{n - 6} - 3n = \frac{3n^2 - 3n(n - 6)}{n - 6} = \frac{3n^2 - 3n^2 - 18n}{n - 6} = \frac{-18n}{n - 6} = \frac{18n}{6 - n}$
Ответ: Г) $\frac{18}{6 - n}$
10. Упростите выражение $\frac{2m + 1}{3m - 2} - \frac{3m^2 + m - 2}{9m^2 - 12m + 4}$.
А) $\frac{1}{(3m - 2)^2}$
Б) $\frac{1}{3m - 2}$
В) $\frac{m}{(3m - 2)^2}$
Г) $\frac{m}{3m - 2}$
Решение:
$\frac{2m + 1}{3m - 2} - \frac{3m^2 + m - 2}{9m^2 - 12m + 4} = \frac{2m + 1}{3m - 2} - \frac{3m^2 + m - 2}{(3m - 2)^2} = \frac{(2m + 1)(3m - 2) - (3m^2 + m - 2)}{(3m - 2)^2} = \frac{6m^2 + 3m - 4m - 2 - 3m^2 - m + 2}{(3m - 2)^2} = \frac{3m^2 - 2m}{(3m - 2)^2} = \frac{m(3m - 2)}{(3m - 2)^2} = \frac{m}{3m - 2}$
Ответ: Г) $\frac{m}{3m - 2}$
11. Упростите выражение $\frac{a - 12}{a^2 + 4a} - \frac{a - 4}{a} + \frac{a}{a + 4}$.
А) $\frac{4}{a}$
Б) $\frac{1}{a}$
В) a
Г) a + 4
Решение:
$\frac{a - 12}{a^2 + 4a} - \frac{a - 4}{a} + \frac{a}{a + 4} = \frac{a - 12}{a(a + 4)} - \frac{a - 4}{a} + \frac{a}{a + 4} = \frac{a - 12 - (a - 4)(a + 4) + a * a}{a(a + 4)} = \frac{a - 12 - (a^2 - 16) + a^2}{a(a + 4)} = \frac{a - 12 - a^2 + 16 + a^2}{a(a + 4)} = \frac{a + 4}{a(a + 4)} = \frac{1}{a}$
Ответ: Б) $\frac{1}{a}$
12. На каком рисунке изображен график функции $y = \frac{x^2 - 4x + 4}{x - 2}$?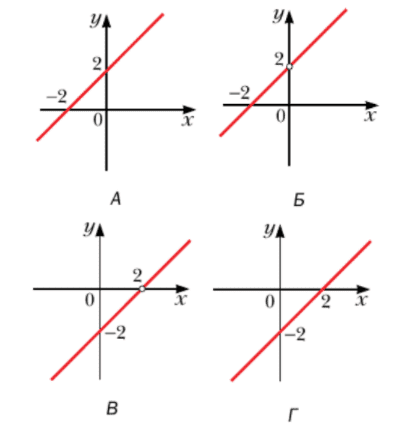
Решение:
$y = \frac{x^2 - 4x + 4}{x - 2} = \frac{(x - 2)^2}{x - 2} = x - 2$
x − 2 ≠ 0
x ≠ 2
Ответ: В

