Ответы к странице 132

513. Упростите выражение:
1) $\sqrt{9a^{16}}$;
2) $\sqrt{0,81d^6}$, если d ≥ 0;
3) $-5\sqrt{4x^2}$, если x ≤ 0;
4) $-0,1\sqrt{100z^{10}}$, если z ≥ 0;
5) $\sqrt{p^6q^8}$, если p ≥ 0;
6) $\sqrt{25m^{34}n^{38}}$, если m ≤ 0, n ≤ 0;
7) $ab^2\sqrt{a^4b^{18}c^{22}}$, если b ≥ 0, c ≤ 0;
8) $-\frac{8m^3p^4}{k^2}\sqrt{\frac{625k^{30}p^{40}}{144m^6}}$, если m <0, k > 0.

Решение:

1) $\sqrt{9a^{16}} = \sqrt{(3a^{8})^2} = |3a^8| = 3a^8$

2) $\sqrt{0,81d^6} = \sqrt{(0,9d^3)^2}= |0,9d^3| = 0,9d^3$, если d ≥ 0

3) $-5\sqrt{4x^2} = -5\sqrt{(2x)^2} = -5 * |2x| = -5 * (-2x) = 10x$, если x ≤ 0

4) $-0,1\sqrt{100z^{10}} = -0,1\sqrt{(10z^{5})^2} = -0,1 * |10z^5| = -0,1 * 10z^5 = -z^5$, если z ≥ 0

5) $\sqrt{p^6q^8} = \sqrt{(p^3q^4)^2} = |p^3q^4| = p^3q^4$, если p ≥ 0

6) $\sqrt{25m^{34}n^{38}} = \sqrt{(5m^{17}n^{19})^2} = |5m^{17}n^{19}| = 5 * (-m^17) * (-n^19) = 5m^{17}n^{19}$, если m ≤ 0, n ≤ 0

7) $ab^2\sqrt{a^4b^{18}c^{22}} = ab^2\sqrt{(a^2b^{9}c^{11})^2} = ab^2 * |a^2b^{9}c^{11}| = ab^2 * a^2b^9 * (-c^{11}) = -a^3b^{11}c^{11}$, если b ≥ 0, c ≤ 0

8) $-\frac{8m^3p^4}{k^2}\sqrt{\frac{625k^{30}p^{40}}{144m^6}} = -\frac{8m^3p^4}{k^2} * \frac{\sqrt{625k^{30}p^{40}}}{\sqrt{144m^6}} = -\frac{8m^3p^4}{k^2} * \frac{\sqrt{(25k^{15}p^{20})^2}}{\sqrt{(12m^3)^2}} = -\frac{8m^3p^4}{k^2} * \frac{|25k^{15}p^{20}|}{|12m^3|} = -\frac{8m^3p^4}{k^2} * \frac{25k^{15}p^{20}}{-12m^3} = \frac{2p^4}{1} * \frac{25k^{13}p^{20}}{3} = \frac{50k^{13}p^{24}}{3}$, если m <0, k > 0

514. Каких из данных равенств выполняются при всех действительных значениях a:
1) $\sqrt{a^2} = a$;
2) $\sqrt{a^4} = a^2$;
3) $\sqrt{a^6} = a^3$;
4) $\sqrt{a^8} = a^4$?

Решение:

1)
$\sqrt{a^2} = a$
$\sqrt{a^2} = |a| = a$
выполняется при a ≥ 0
2)
$\sqrt{a^4} = a^2$
$\sqrt{a^4} = \sqrt{(a^2)^2} = |a^2| = a^2$
выполняется при любых значениях a
3)
$\sqrt{a^6} = a^3$
$\sqrt{a^6} = \sqrt{(a^3)^2} = |a^3| = a^3$
выполняется при a ≥ 0
4)
$\sqrt{a^8} = a^4$
$\sqrt{a^8} = \sqrt{(a^4)^2} = |a^4| = a^4$
выполняется при любых значениях a
Ответ: при любых значениях a выполняются равенства 2 и 4

515. При каких значениях a выполняется равенство:
1) $\sqrt{a^{10}} = a^5$;
2) $\sqrt{a^{10}} = -a^5$;
3) $\sqrt{a^2} = (\sqrt{a})^2$;
4) $\sqrt{a^2} = (\sqrt{-a})^2$?

Решение:

1) $\sqrt{a^{10}} = \sqrt{(a^{5})^2} = |a^5| = a^5$ − выполняется при a ≥ 0

2) $\sqrt{a^{10}} = \sqrt{(a^{5})^2} = |a^5| = -a^5$ − выполняется при a ≤ 0

3) $\sqrt{a^2} = (\sqrt{a})^2$
подкоренное выражение должно быть неотрицательным, тогда:
a ≥ 0, значит равенство выполняется при a ≥ 0

4) $\sqrt{a^2} = (\sqrt{-a})^2$
подкоренное выражение должно быть неотрицательным, тогда:
−a ≥ 0
a ≤ 0, значит равенство выполняется при a ≤ 0

516. Постройте график функции:
1) $y = \sqrt{x^{2}} - x$, если x ≤ 0;
2) $y = 2x + \sqrt{x^{2}}$;
3) $y = \sqrt{x} * \sqrt{x}$;
4) $y = \frac{x^2}{\sqrt{x^2}} + 3$.

Решение:

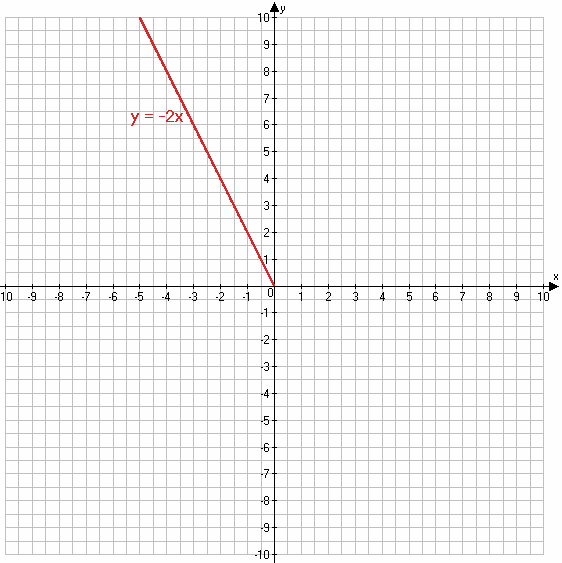
1) $y = \sqrt{x^{2}} - x$, если x ≤ 0
$y = \sqrt{x^{2}} - x = |x| - x = -x - x = -2x$
y = −2x
х -1 0
у 2 0


2) $y = 2x + \sqrt{x^{2}} = 2x + |x|$
если x ≥ 0, то:
y = 2x + x = 3x
х 0 1
у 0 3
если x < 0, то:
y = 2x − x = x
х -2 -1
у -2 -1


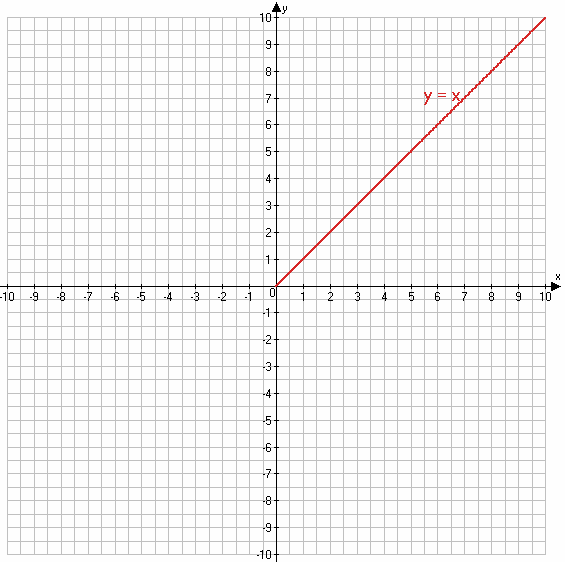
3) $y = \sqrt{x} * \sqrt{x} = (\sqrt{x})^2 = x$ при x ≥ 0
y = x
х 1 2
у 1 2


4) $y = \frac{x^2}{\sqrt{x^2}} + 3 = \frac{x^2}{|x|} + 3$ при x ≠ 0
если x > 0, то:
$y = \frac{x^2}{x} + 3 = x + 3$
х 1 2
у 4 5
если x < 0, то:
$y = \frac{x^2}{-x} + 3 = -x + 3$
х -2 -1
у 5   4

517. Постройте график функции:
1) $y = \sqrt{x^2} - 2x$, если x ≥ 0;
2) $y = \sqrt{-x} - \sqrt{-x}$.

Решение:

1) $y = \sqrt{x^2} - 2x = |x| - 2x$
если x ≥ 0, то:
$y = |x| - 2x = x - 2x = -x$
y = −x
х 0 1
у 0 -1


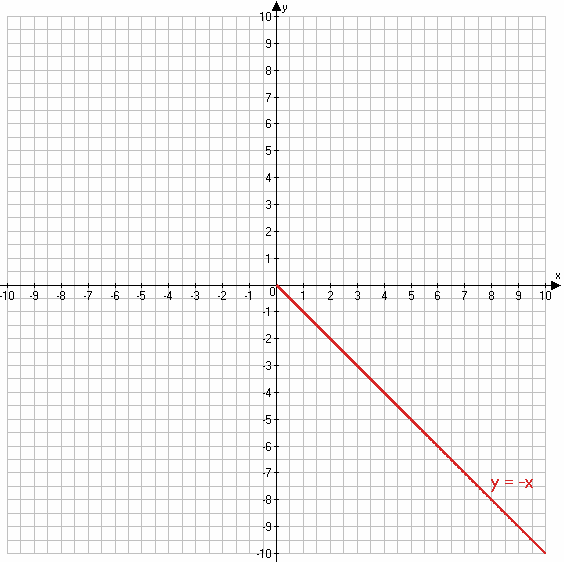
2) $y = \sqrt{-x} - \sqrt{-x} = (\sqrt{-x})^2 = -x$ при x ≤ 0
y = −x
х 0 -1
у 0 1

518. При каком значении x выполняется равенство:
1) $\sqrt{x^2} = x - 4$;
2) $\sqrt{x^2} = 6 - x$;
3) $2\sqrt{x^2} = x + 3$?

Решение:

1) $\sqrt{x^2} = x - 4$
|x| = x − 4
x − 4 ≥ 0
x ≥ 4
при x ≥ 0:
x = x − 4
x − x = −4
0 = −4 − нет корней
при x < 0:
−x = x − 4
−x − x = −4
−2x = −4
x = 2 < 4 − нет корней
Ответ: нет корней

2) $\sqrt{x^2} = 6 - x$
|x| = 6 − x
6 − x ≥ 0
−x ≥ −6
x ≤ 6
при x ≥ 0:
x = 6 − x
x + x = 6
2x = 6
x = 3 ≤ 6
при x < 0:
−x = 6 − x
−x + x = 6
0 = 6 − нет корней
Ответ: при x = 3

3) $2\sqrt{x^2} = x + 3$
2 * |x| = x + 3
|x| = 0,5x + 1,5
0,5x + 1,5 ≥ 0
0,5x ≥ −1,5
x ≥ −3
при x ≥ 0:
2x = x + 3
2x − x = 3
x = 3 ≥ −3
при x < 0:
2 * (−x) = x + 3
−2x = x + 3
−2x − x = 3
−3x = 3
x = −1 ≥ −3
Ответ: при x = −1 и при x = 3

519. Решите уравнение:
1) $\sqrt{x^2} = x + 8$;
2) $\sqrt{x^2} = 6x - 10$.

Решение:

1) $\sqrt{x^2} = x + 8$
|x| = x + 8
x + 8 ≥ 0
x ≥ −8
при x ≥ 0:
x = x + 8
x − x = 8
0 = 8 − нет корней
при x < 0:
−x = x + 8
−x − x = 8
−2x = 8
x = −4 ≥ −8
Ответ: при x = −4

2) $\sqrt{x^2} = 6x - 10$
|x| = 6x − 10
6x − 10 ≥ 0
6x ≥ 10
$x ≥ \frac{10}{6} = \frac{5}{3} = 1\frac{2}{3}$
при x ≥ 0:
x = 6x − 10
x − 6x = −10
−5x = −10
$x = 2 ≥ 1\frac{2}{3}$
при x < 0:
−x = 6x − 10
−x − 6x = −10
−7x = −10
$x = \frac{10}{7} = 1\frac{3}{7} ≤ 1\frac{2}{3}$ − нет корней
Ответ: при x = 2

520. Найдите значение выражения:
$(\frac{a^2 - 5a}{a^2 - 10a + 25} + \frac{25}{a^2 - 25}) : \frac{125 - a^3}{5 + a}$
при a = 4,5.

Решение:

$(\frac{a^2 - 5a}{a^2 - 10a + 25} + \frac{25}{a^2 - 25}) : \frac{125 - a^3}{5 + a} = (\frac{a(a - 5)}{(a - 5)^2} + \frac{25}{(a - 5)(a + 5)}) : \frac{125 - a^3}{a + 5} = (\frac{a}{a - 5} + \frac{25}{(a - 5)(a + 5)}) * \frac{a + 5}{125 - a^3} = \frac{a(a + 5) + 25}{(a - 5)(a + 5)} * \frac{a + 5}{125 - a^3} = \frac{a^2 + 5a + 25}{a - 5} * \frac{1}{(5 - a)(25 + 5a + a^2)} = \frac{1}{a - 5} * \frac{1}{5 - a} = \frac{1}{a - 5} * (-\frac{1}{a - 5}) = -\frac{1}{(a - 5)^2}$
при a = 4,5:
$-\frac{1}{(4,5 - 5)^2} = -\frac{1}{(-0,5)^2} = -\frac{1}{(\frac{1}{2})^2} = -\frac{1}{\frac{1}{4}} = -4$