Ответы к странице 82
327. Проволочный реостат (рис.9) подключен к блоку питания. Сопротивление реостата R зависит от положения ползунка и может изменяться в пределах от 0 до 6 Ом. Пользуясь графиком зависимости силы тока I от сопротивления R (рис.10), при условии, что напряжение на концах реостата остается неизменным, определите:
1) чему равна сила тока, если сопротивление равно 2 Ом;
2) при каком значении сопротивления сила тока равна 3 А;
3) сколько вольт составляет напряжение на концах реостата.
Решение:
1) При сопротивлении 2 Ом, сила тока равна 6 А.
2) При силе тока 3 А, сопротивление равно 4 Ом.
3) При силе тока 3 А, сопротивление равно 4 Ом, тогда:
3 * 4 = 12 (Вольт) − составляет напряжение на концах реостата.
328. Найдите значение k, при котором график функции $y = \frac{k}{x}$ проходит через точку:
1) A(−5; 4);
2) $B(\frac{1}{6}; -2)$;
3) C(1,5; −8).
Решение:
1) $y = \frac{k}{x}$
A(−5; 4)
$4 = \frac{k}{-5}$
k = 4 * (−5)
k = −20
2) $y = \frac{k}{x}$
$B(\frac{1}{6}; -2)$
$-2 = \frac{k}{\frac{1}{6}}$
$k = -2 * \frac{1}{6}$
$k = -\frac{1}{3}$
3) $y = \frac{k}{x}$
C(1,5; −8)
$-8 = \frac{k}{1,5}$
k = 1,5 * (−8)
k = −12
329. График функции $y = \frac{k}{x}$ проходит через точку A(10;1,6). Проходит ли график этой функции через точку:
1) B(−1;−16);
2) C(−2;8)?
Решение:
$y = \frac{k}{x}$
A(10;1,6)
$1,6 = \frac{k}{10}$
k = 10 * 1,6
k = 16, значит функция равна $y = \frac{16}{x}$, тогда:
1)
$y = \frac{16}{x}$
B(−1;−16)
$-16 = \frac{16}{-1}$
−16 = −16, значит график функции $y = \frac{k}{x}$ проходит через точку B(−1;−16).
2)
$y = \frac{16}{x}$
C(−2;8)
$8 = \frac{16}{-2}$
8 ≠ −8, значит график функции $y = \frac{k}{x}$ не проходит через точку C(−2;8).
330. Постройте в одной системе координат график функций $y = \frac{4}{x}$ и y = x и определите координаты точек их пересечения.
Решение:
$y = \frac{4}{x}$
х -4 -2 -1 -0,5 0,5 1 2 4
у -1 -2 -4 -8 8 4 2 1
y = x
х 1 2
у 1 2

Ответ: графики данных функций пересекаются в точках A(2; 2) и B(−2; −2)
331. Решите графически уравнение:
1) $\frac{4}{x} = 4 - x$;
2) $x - 2 = \frac{3}{x}$;
3) $x + 2 = -\frac{5}{x}$.
Решение:
1) $\frac{4}{x} = 4 - x$
$y = \frac{4}{x}$
х -4 -2 -1 -0,5 0,5 1 2 4
у -1 -2 -4 -8 8 4 2 1
y = 4 − x
х 1 2
у 3 2
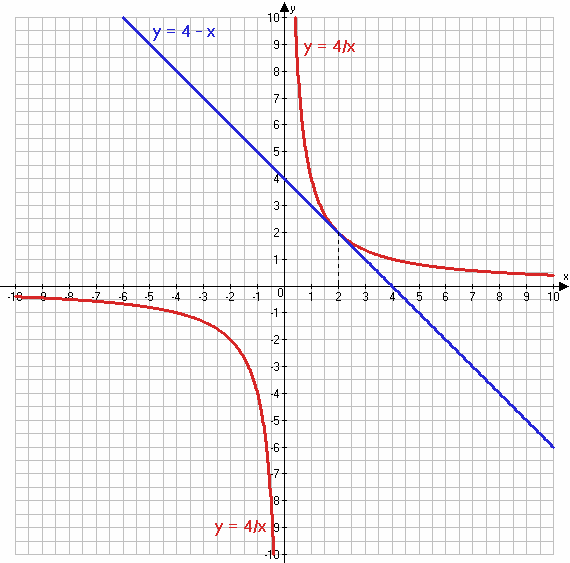
Ответ: x = 2
2) $x - 2 = \frac{3}{x}$
y = x − 2
х 1 2
у -1 2
$y = \frac{3}{x}$
х -3 -2 -1 -0,5 0,5 1 2 3
у -1 -1,5 -3 -6 6 3 1,5 1
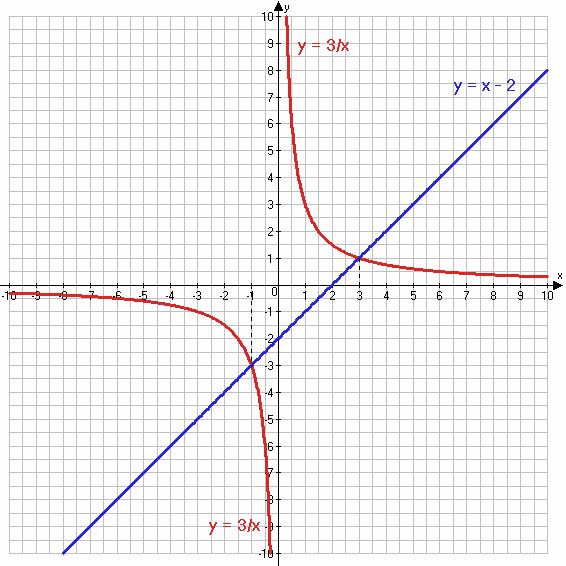
Ответ: x = −1 и x = 3
3) $x + 2 = -\frac{5}{x}$
y = x + 2
х 1 2
у 3 4
$y = -\frac{5}{x}$
х -5 -2 -1 -0,5 0,5 1 2 5
у 1 2,5 5 10 10 -5 -2,5 -1

Ответ: нет корней
332. Решите графически уравнение:
1) $\frac{8}{x} = 6 - x$;
2) $2x = \frac{2}{x}$;
3) $\frac{7}{x} = -x$.
Решение:
1) $\frac{8}{x} = 6 - x$
$y = \frac{8}{x}$
х -8 -4 -2 -1 1 2 4 8
у -1 -2 -4 -8 8 4 2 1
y = 6 − x
х 1 2
у 5 4
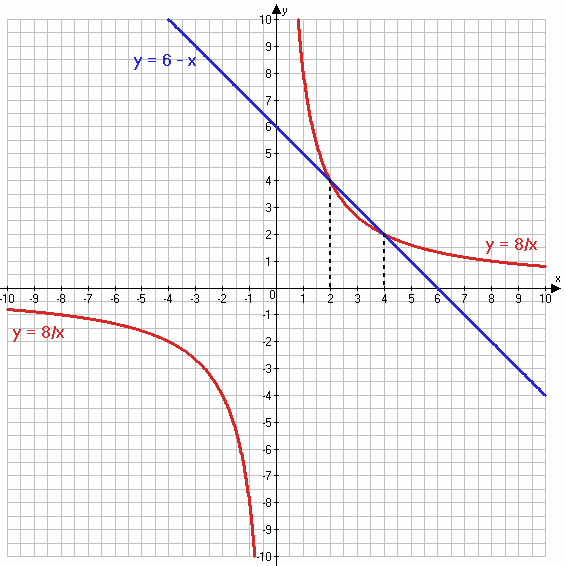
Ответ: x = 2 и x = 4
2) $2x = \frac{2}{x}$
y = 2x
х 1 2
у 2 4
$y = \frac{2}{x}$
х -2 -1 -0,5 -0,25 0,25 0,5 1 2
у -1 -2 -4 -8 8 4 2 1
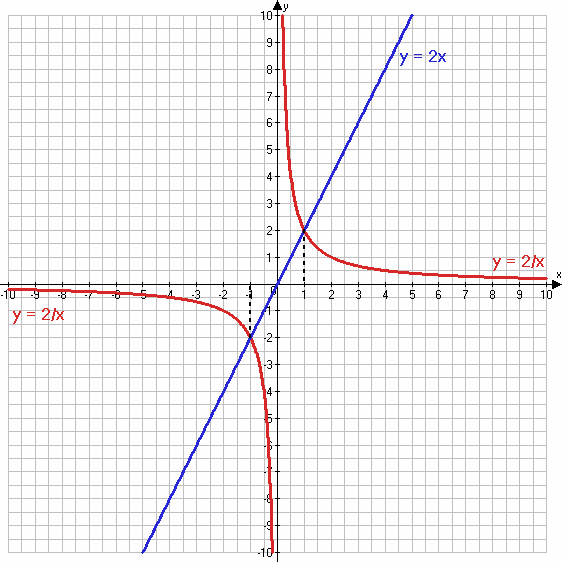
Ответ: x = −1 и x = 1
3) $\frac{7}{x} = -x$
$y = \frac{7}{x}$
х -7 -3,5 -2 -1 1 2 3,5 7
y = −x
х 1 2
у -1 -2
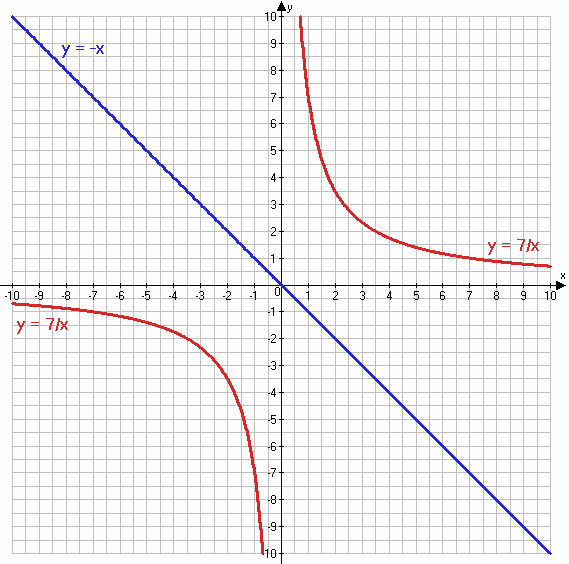
Ответ: нет корней
333. Решите графически систему уравнений:
1)
$\begin{equation*} \begin{cases} xy = 4 &\\ 4y = x & \end{cases} \end{equation*}$
2)
$\begin{equation*} \begin{cases} x - y = 1 &\\ xy = 2 & \end{cases} \end{equation*}$
Решение:
1) $\begin{equation*} \begin{cases} xy = 4 &\\ 4y = x & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = \frac{4}{x} &\\ y = \frac{x}{4} & \end{cases} \end{equation*}$
$y = \frac{4}{x}$
$y = \frac{x}{4}$

Ответ: (−4; −1); (4; 1).
2) $\begin{equation*} \begin{cases} x - y = 1 &\\ xy = 2 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = x - 1 &\\ y = \frac{2}{x} & \end{cases} \end{equation*}$
y = x − 1
$y = \frac{2}{x}$

Ответ: (−1; −2); (2; 1).

