Ответы к странице 83

334. Решите графически систему уравнений:
$\begin{equation*} \begin{cases} xy = 5 &\\ y - x = 4 & \end{cases} \end{equation*}$

Решение:

$\begin{equation*} \begin{cases} xy = 5 &\\ y - x = 4 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = \frac{5}{x} &\\ y = x + 4 & \end{cases} \end{equation*}$

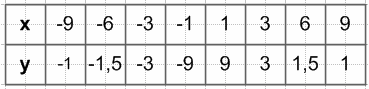
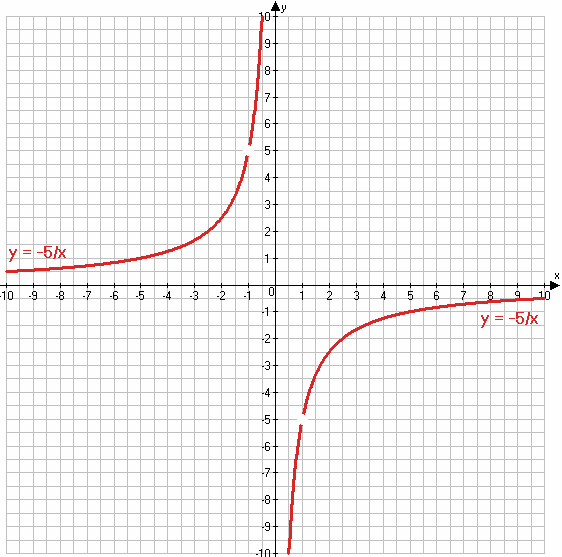
$y = \frac{5}{x}$

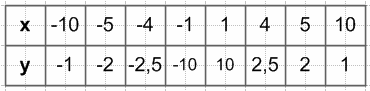
y = x + 4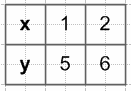

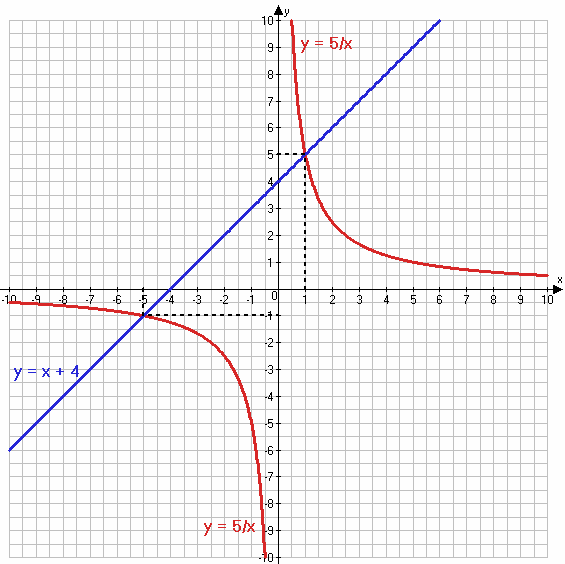
Ответ: (−5; −1); (1; 5).

335. Определите графически количество решений системы уравнений:
1)  $\begin{equation*} \begin{cases} xy = -1 &\\ x + 3y = 0 & \end{cases} \end{equation*}$
2)  $\begin{equation*} \begin{cases} xy = -1 &\\ x - 3y = 0 & \end{cases} \end{equation*}$
3)  $\begin{equation*} \begin{cases} xy = 6 &\\ 3x - 2y = 6 & \end{cases} \end{equation*}$

Решение:

1) $\begin{equation*} \begin{cases} xy = -1 &\\ x + 3y = 0 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = -\frac{1}{x} &\\ 3y = -x & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = -\frac{1}{x} &\\ y = -\frac{x}{3} & \end{cases} \end{equation*}$

$y = -\frac{1}{x}$

$y = -\frac{x}{3}$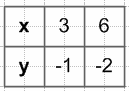

Ответ: система уравнений имеет 2 решения

2) $\begin{equation*} \begin{cases} xy = -1 &\\ x - 3y = 0 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = -\frac{1}{x} &\\ 3y = x & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = -\frac{1}{x} &\\ y = \frac{x}{3} & \end{cases} \end{equation*}$

$y = -\frac{1}{x}$

$y = \frac{x}{3}$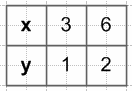

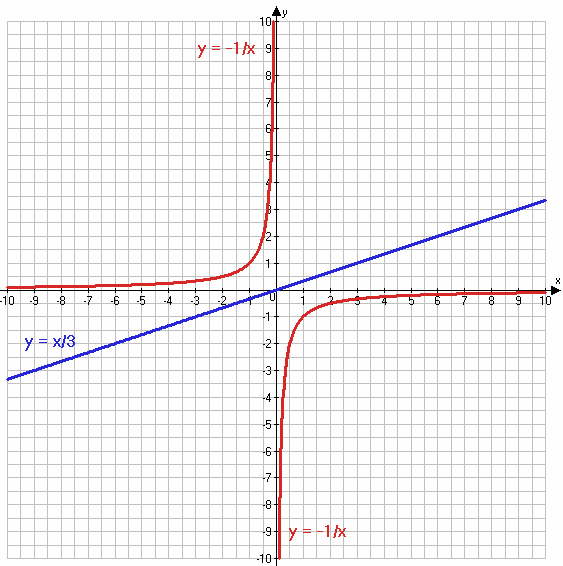
Ответ: система уравнений не имеет решений

3) $\begin{equation*} \begin{cases} xy = 6 &\\ 3x - 2y = 6 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = \frac{6}{x} &\\ 2y = 3x - 6 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = \frac{6}{x} &\\ y = 1,5x - 3 & \end{cases} \end{equation*}$

$y = \frac{6}{x}$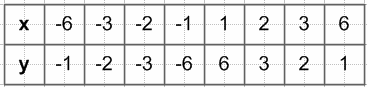

y = 1,5x − 3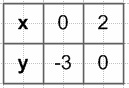

Ответ: система уравнений имеет 2 решения

336. Определите графически количество решений системы уравнений:
$\begin{equation*} \begin{cases} xy = -8 &\\ 2x + 3y = 6 & \end{cases} \end{equation*}$

Решение:

$\begin{equation*} \begin{cases} xy = -8 &\\ 2x + 3y = 6 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = -\frac{8}{x} &\\ 3y = 6 - 2x & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} y = -\frac{8}{x} &\\ y = 2 - \frac{2}{3}x & \end{cases} \end{equation*}$

$y = -\frac{8}{x}$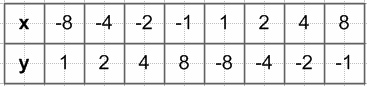

$y = 2 - \frac{2}{3}x$

Ответ: система уравнений имеет 2 решения

337. Найдите координаты всех точек графика функции $y = \frac{64}{x}$, у которых абсцисса и ордината равны.

Решение:

$y = \frac{64}{x}$
x = y
Тогда:
$x = \frac{64}{x}$
$x - \frac{64}{x} = 0 |* x$
$x^2 - 64 = 0$
$x^2 = 64$
x = ±8
при x = 8: $y = \frac{64}{8} = 8$;
при x = −8: $y = \frac{64}{-8} = -8$.
Ответ: (−8; −8) и (8; 8).

338. Найдите координаты всех точек графика функции $y = -\frac{25}{x}$, у которых абсцисса и ордината − противоположные числа.

Решение:

$y = -\frac{25}{x}$
y = −x
Тогда:
$-x = -\frac{25}{x}$
$-x + \frac{25}{x} = 0 |* x$
$-x^2 + 25 = 0$
$x^2 = 25$
x = ±5
при x = −5: $y = -\frac{25}{-5} = 5$;
при x = 5: $y = -\frac{25}{5} = -5$.
Ответ: (−5; 5) и (5; −5)

339. Постройте график функции $y = \frac{6}{|x|}$.

Решение:

$y = \frac{6}{|x|}$
$y = \begin{equation*} \begin{cases} \frac{6}{x}, x > 0 &\\ \frac{6}{-x}, x < 0 & \end{cases} \end{equation*}$

$y = \frac{6}{|x|}$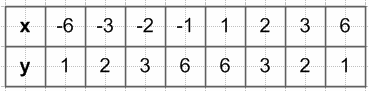

340. Постройте график функции:
1)
$y = \begin{equation*} \begin{cases} -\frac{2}{x}, если\;x ≤ -1 &\\ x + 3, если\;x > - 1 & \end{cases} \end{equation*}$
2)
$y = \begin{equation*} \begin{cases} -2x + 10, если\;x ≤ 2 &\\ \frac{12}{x}, если\;2 < x < 4 &\\ 3, если\;x ≥ 4 & \end{cases} \end{equation*}$

Решение:

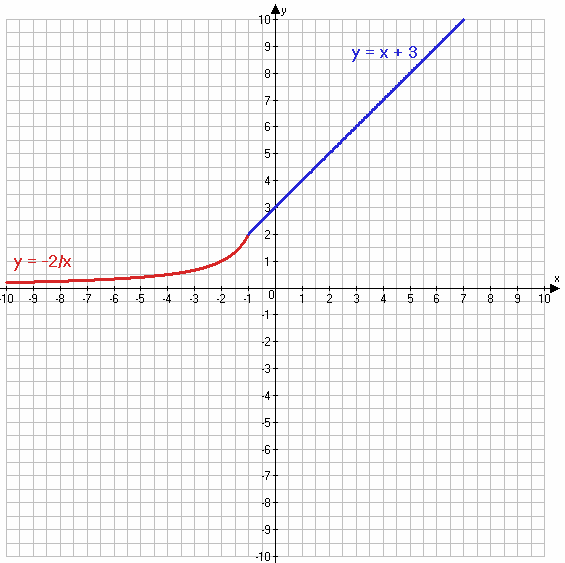
1) $y = \begin{equation*} \begin{cases} -\frac{2}{x}, если\;x ≤ -1 &\\ x + 3, если\;x > - 1 & \end{cases} \end{equation*}$

$y = -\frac{2}{x}$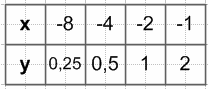

y = x + 3

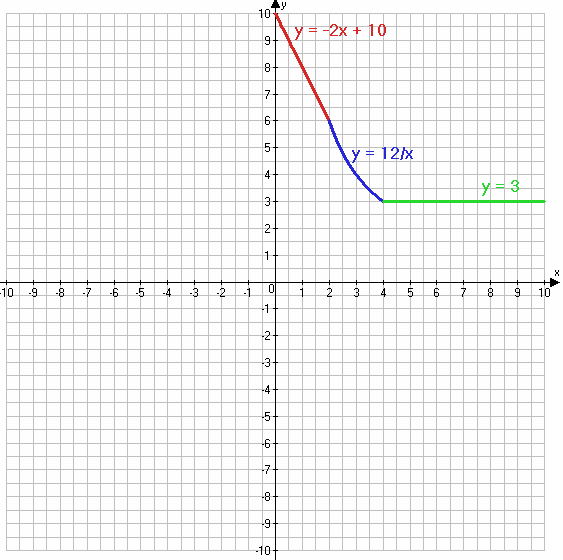
2) $y = \begin{equation*} \begin{cases} -2x + 10, если\;x ≤ 2 &\\ \frac{12}{x}, если\;2 < x < 4 &\\ 3, если\;x ≥ 4 & \end{cases} \end{equation*}$

y = −2x + 10, если x ≤ 2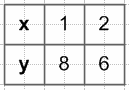

$y = \frac{12}{x}$, если 2 < x < 4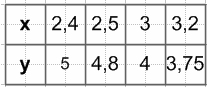

341. Постройте график функции:
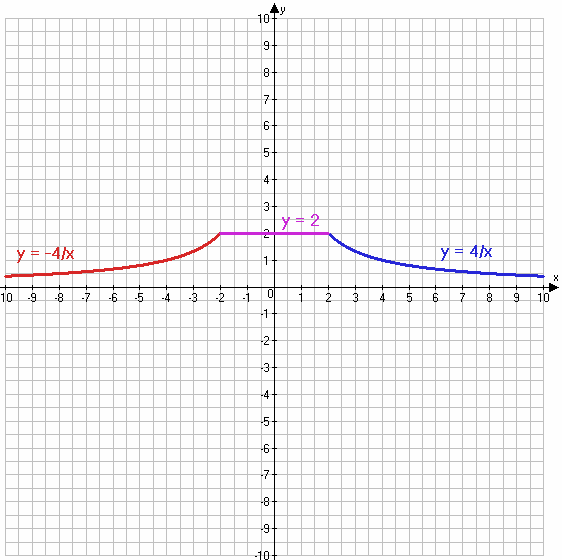
$y = \begin{equation*} \begin{cases} -\frac{4}{x}, если\;x < -2 &\\ 2, если\;-2 ≤ x ≤ 2 &\\ \frac{4}{x}, если\;x > 2 & \end{cases} \end{equation*}$

Решение:

$y = \begin{equation*} \begin{cases} -\frac{4}{x}, если\;x < -2 &\\ 2, если\;-2 ≤ x ≤ 2 &\\ \frac{4}{x}, если\;x > 2 & \end{cases} \end{equation*}$

$-\frac{4}{x}$, если x < −2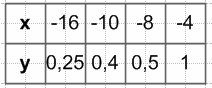

$\frac{4}{x}$, если x > 2

342. Постройте график функции:
1) $y = \frac{9x - 18}{x^2 - 2x}$;
2) $y = \frac{5x^2 - 5}{x - x^3}$.

Решение:

1) $y = \frac{9x - 18}{x^2 - 2x} = \frac{9(x - 2)}{x(x - 2)} = \frac{9}{x}$
x(x − 2) ≠ 0
x ≠ 0
и
x − 2 ≠ 0
x ≠ 2



2) $y = \frac{5x^2 - 5}{x - x^3} = \frac{5(x^2 - 1)}{x(1 - x^2)} = -\frac{5(x^2 - 1)}{x(x^2 - 1)} = -\frac{5}{x}$
$x(x^2 - 1) ≠ 0$
x ≠ 0
и
$x^2 - 1 ≠ 0$
$x^2 ≠ 1$
x ≠ ±1

343. Постройте график функции
$y = \frac{10x^2 - 40}{x^3 - 4x}$

Решение:

$y = \frac{10x^2 - 40}{x^3 - 4x} = \frac{10(x^2 - 4)}{x(x^2 - 4)} = \frac{10}{x}$
$x(x^2 - 4) ≠ 0$
x ≠ 0
и
$x^2 - 4 ≠ 0$
$x^2 ≠ 4$
x ≠ ±2

344. Докажите, что при всех допустимых значениях переменных, содержащихся в выражении, его значение не зависит от значений a и b:
$\frac{a^2 - b^2}{a + 3b} * (\frac{a + b}{a^2 - 2ab + b^2} + \frac{b}{a^2 - b^2}) - \frac{b}{a - b}$.

Решение:

$\frac{a^2 - b^2}{a + 3b} * (\frac{a + b}{a^2 - 2ab + b^2} + \frac{b}{a^2 - b^2}) - \frac{b}{a - b} = \frac{(a - b)(a + b)}{a + 3b} * (\frac{a + b}{(a - b)^2} + \frac{b}{(a - b)(a + b)}) - \frac{b}{a - b} = \frac{(a - b)(a + b)}{a + 3b} * \frac{(a + b)^2 + b(a - b)}{(a - b)^2(a + b)} - \frac{b}{a - b} = \frac{1}{a + 3b} * \frac{a^2 + 2ab + b^2 + ab - b^2}{a - b} - \frac{b}{a - b} = \frac{1}{a + 3b} * \frac{a^2 + 3ab}{a - b} - \frac{b}{a - b} = \frac{1}{a + 3b} * \frac{a(a + 3b)}{a - b} - \frac{b}{a - b} = \frac{a}{a - b} - \frac{b}{a - b} = \frac{a - b}{a - b} = 1$, следовательно значение выражения не зависит от значения переменных.