Ответы к странице 18

53. Найдите значение выражения
$\frac{2m - 1,5n}{32m^2 - 18n^2}$, если 4m + 3n = 8.

Решение:

$\frac{2m - 1,5n}{32m^2 - 18n^2} = \frac{0,5(4m - 3n)}{2(16m^2 - 9n^2)} = \frac{0,5(4m - 3n)}{2(4m - 3n)(4m + 3n)} = \frac{\frac{1}{2}}{2(4m + 3n)} = \frac{1}{2} * \frac{1}{2(4m + 3n)} = \frac{1}{4(4m + 3n)}$
при 4m + 3n = 8:
$\frac{1}{4 * 8} = \frac{1}{32}$

54. Существует ли такое значение a, при котором дробь
$\frac{a^3 - a^2 - a + 1}{a^3 + a^2 + a + 1}$
принимает отрицательное значение?

Решение:

$\frac{a^3 - a^2 - a + 1}{a^3 + a^2 + a + 1} = \frac{(a^3 - a^2) - (a - 1)}{(a^3 + a^2) + (a + 1)} = \frac{a^2(a - 1) - (a - 1)}{a^2(a + 1) + (a + 1)} = \frac{(a - 1)(a^2 - 1)}{(a + 1)(a^2 + 1)} = \frac{(a - 1)(a - 1)(a + 1)}{(a + 1)(a^2 + 1)} = \frac{(a - 1)^2}{a^2 + 1} ≥ 0$, так как:
$(a - 1)^2 ≥ 0$, так как квадрат любого числа не может быть отрицательным;
$a^2 + 1 > 0$, так как сумма двух положительных чисел всегда больше 0.
Ответ: не существует такого значения a, при котором дробь принимает отрицательное значение.

55. Постройте график функции:
1) $y = \frac{x^2 - 4}{x + 2}$;
2) $y = \frac{x - 3}{3 - x}$;
3) $y = \frac{x^2 - 10x + 25}{x - 5} - \frac{2x^2 - 4x}{x}$;
4) $y = \frac{2}{x + 4} - \frac{2}{x + 4}$.

Решение:

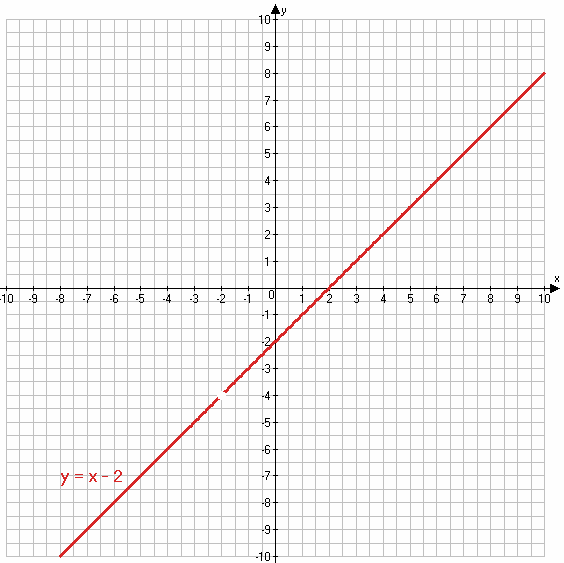
1) $y = \frac{x^2 - 4}{x + 2} = \frac{(x - 2)(x + 2)}{x + 2} = x - 2$
x + 2 ≠ 0
x ≠ −2
х 4 5
у 2 3


2) $y = \frac{x - 3}{3 - x} = -\frac{x - 3}{x - 3} = -1$
3 − x ≠ 0
x ≠ 3


3) $y = \frac{x^2 - 10x + 25}{x - 5} - \frac{2x^2 - 4x}{x} = \frac{(x - 5)^2}{x - 5} - \frac{2x(x - 2)}{x} = x - 5 - 2(x - 2) = x - 5 - 2x + 4 = -x - 1$
x − 5 ≠ 0
x ≠ 5
и
x ≠ 0
х 2 3
у -3 -4


4) $y = \frac{2}{x + 4} - \frac{2}{x + 4} = 0$
x + 4 ≠ 0
x ≠ −4

56. Постройте график функции:
1) $y = \frac{x^2 - 8x + 16}{x - 4}$;
2) $y = x - \frac{x}{x}$;
3) $y = \frac{x^2 - 3x}{x} - \frac{2x^2 - 2}{x^2 - 1}$.

Решение:

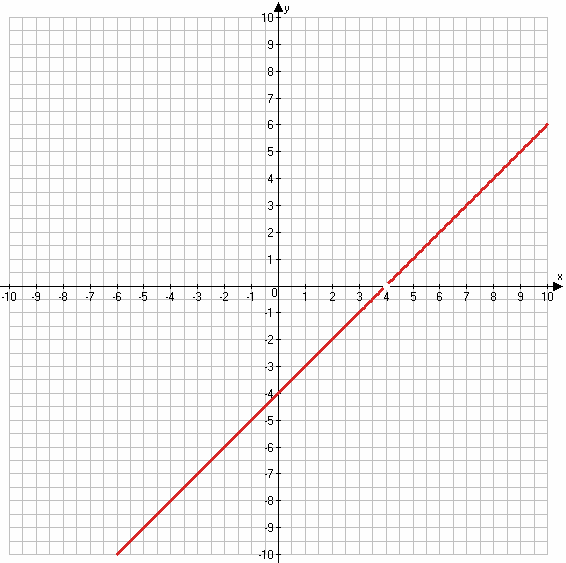
1) $y = \frac{x^2 - 8x + 16}{x - 4} = \frac{(x - 4)^2}{x - 4} = x - 4$
x − 4 ≠ 0
x ≠ 4
х 5 6
у 1 2


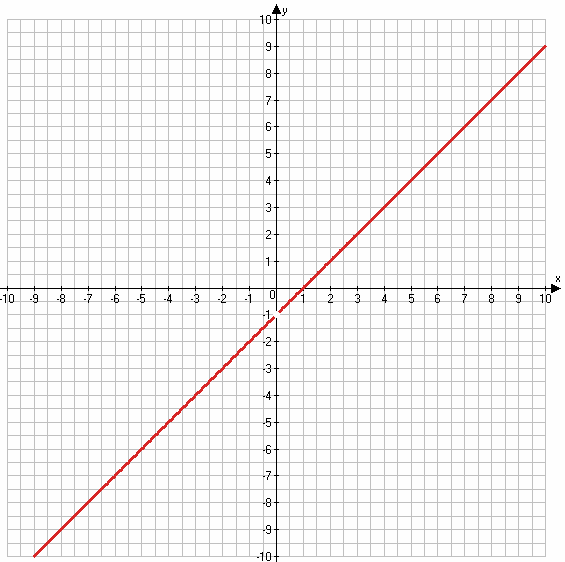
2) $y = x - \frac{x}{x} = x - 1$
x ≠ 0
х 5 6
у 4 5


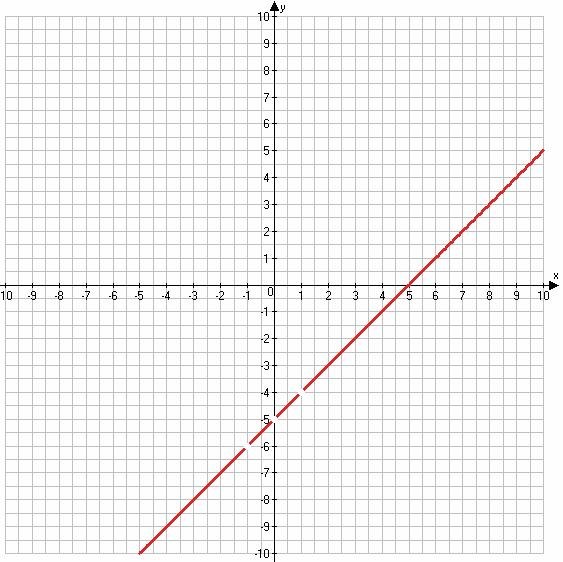
3) $y = \frac{x^2 - 3x}{x} - \frac{2x^2 - 2}{x^2 - 1} = \frac{x(x - 3)}{x} - \frac{2(x^2 - 1)}{x^2 - 1} = x - 3 - 2 = x - 5$
x ≠ 0
и
$x^2 - 1 ≠ 0$
$x^2 ≠ 1$
x ≠ ±1
х 5 6
у 0 1

57. Постройте график функции:
1) $y = \frac{|x|}{x}$;
2) $y = \frac{x^2 - 1}{|x| - 1}$.

Решение:

1) $y = \frac{|x|}{x}$
$y = \begin{equation*} \begin{cases} 1, x > 0 &\\ -1, x < 0 & \end{cases} \end{equation*}$
x ≠ 0


2) $y = \frac{x^2 - 1}{|x| - 1} = \frac{(x - 1)(x + 1)}{|x| - 1}$
$y = \begin{equation*} \begin{cases} x + 1, x ≥ 0 &\\ 1 - x, x < 0 & \end{cases} \end{equation*}$
|x| − 1 ≠ 0
|x| ≠ 1
x ≠ ±1
y = x + 1
х 2 3
у 3 4
y = 1 − x
х 2 3
у -1 -2

58. Решите уравнение:
1) $\frac{x + 1}{x + 1} = 1$;
2) $\frac{x^2 - 25}{x - 5} = 10$;
3) $\frac{x + 6}{|x| - 6} = 0$.

Решение:

1) $\frac{x + 1}{x + 1} = 1$
1 = 1
x + 1 ≠ 0
x ≠ −1
Ответ: x − любое число, кроме x = −1

2) $\frac{x^2 - 25}{x - 5} = 10$
x − 5 ≠ 0
x ≠ 5
$\frac{(x - 5)(x + 5)}{x - 5} = 10$
x + 5 = 10
x = 10 − 5
x = 5 − не подходит.
Ответ: нет корней

3) $\frac{x + 6}{|x| - 6} = 0$
|x| − 6 ≠ 0
|x| ≠ 6
x ≠ ±6
при x > 0:
x + 6 = 0
x = −6 − не подходит
при x < 0:
$\frac{x + 6}{-(x + 6)} = 0$
−1 ≠ 0
Ответ: нет корней

59. Решите уравнение:
1) $\frac{x^2 - 16}{x + 4} = -8$;
2) $\frac{|x| - 7}{x - 7} = 0$.

Решение:

1) $\frac{x^2 - 16}{x + 4} = -8$
x + 4 ≠ 0
x ≠ − 4
$\frac{(x - 4)(x + 4)}{x + 4} = -8$
x − 4 = −8
x = −8 + 4
x = −4 − не подходит.
Ответ: нет корней

2) $\frac{|x| - 7}{x - 7} = 0$
x − 7 ≠ 0
x ≠ 7
при x > 0:
$\frac{x - 7}{x - 7} = 0$
1 ≠ 0
при x < 0:
$\frac{-x - 7}{x - 7} = 0$
−x − 7 = 0
x = −7
Ответ: x = −7

60. Для каждого значения a решите уравнение:
1) ax = 1;
2) ax = a;
3) $(a - 6)x = a^2 - 12a + 36$;
4) $(a^2 - 4)x = a - 2$.

Решение:

1) ax = 1
при a = 0:
0x = 1
0 ≠ 1 − корней нет
при a ≠ 0:
$x = \frac{1}{a}$

2) ax = a
при a = 0:
0x = 0
0 = 0, x − любое число.
при a ≠ 0:
$x = \frac{a}{a} = 1$

3) $(a - 6)x = a^2 - 12a + 36$
$(a - 6)x = (a - 6)^2$
при a = 6:
$(6 - 6)x = (6 - 6)^2$
0x = 0
0 = 0, x − любое число.
при a ≠ 6:
$x = \frac{(a - 6)^2}{a - 6} = a - 6$

4) $(a^2 - 4)x = a - 2$
(a − 2)(a + 2)x = a − 2
при a = 2:
(2 − 2)(2 + 2)x = 2 − 2
0x = 0
0 = 0, x − любое число.
при a = −2:
(−2 − 2)(−2 + 2)x = −2 − 2
0x = −4
0 ≠ −4 − нет корней.
при a ≠ ±2:
$x = \frac{a - 2}{(a - 2)(a + 2)} = \frac{1}{a + 2}$

61. Для каждого значения a решите уравнение:
1) (a + 3)x = 3;
2) $(a^2 - 9a)x = a^2 - 18a + 81$.

Решение:

1) (a + 3)x = 3
при a = −3:
(−3 + 3)x = 3
0x = 3
0 ≠ 3 − нет корней.
при a ≠ −3:
$x = \frac{3}{a + 3}$

2) $(a^2 - 9a)x = a^2 - 18a + 81$
$a(a - 9)x = (a - 9)^2$
при a = 0:
$0(0 - 9)x = (0 - 9)^2$
0x = 81
0 ≠ 81 − нет корней.
при 9 = 0:
$9(9 - 9)x = (9 - 9)^2$
0x = 0
0 = 0, x − любое число.
при a ≠ 0, a ≠ 9:
$x = \frac{(a - 9)^2}{a(a - 9)} = \frac{a - 9}{a}$

62. Упростите выражение:
1) (x + 2)(x − 9) − 3x(3 − 2x);
2) (a + 5)(a − 2) + (a + 4)(a − 5);
3) (y − 8)(2y + 1) − (3y + 1)(y − 6);
4) (2x − 3y)(2x + 3y) + (3x + 2y)(3x − 2y);
5) $(x + 1)^2 - (x - 3)(x + 3)$;
6) $(y - 4)(y + 3) - (y - 6)^2$.

Решение:

1) $(x + 2)(x - 9) - 3x(3 - 2x) = x^2 + 2x - 9x - 18 - 9x + 6x^2 = 7x^2 - 16x - 18$

2) $(a + 5)(a - 2) + (a + 4)(a - 5) = a^2 + 5a - 2a - 10 + a^2 + 4a - 5a - 20 = 2a^2 + 2a - 30$

3) $(y - 8)(2y + 1) - (3y + 1)(y - 6) = 2y^2 - 16y + y - 8 - (3y^2 + y - 18y - 6) = 2y^2 - 15y - 8 - (3y^2 - 17y - 6) = 2y^2 - 15y - 8 - 3y^2 + 17y + 6 = -y^2 + 2y - 2$

4) $(2x - 3y)(2x + 3y) + (3x + 2y)(3x - 2y) = 4x^2 - 9y^2 + 9x^2 - 4y^2 = 13x^2 - 13y^2$

5) $(x + 1)^2 - (x - 3)(x + 3) = x^2 + 2x + 1 - (x^2 - 9) = x^2 + 2x + 1 - x^2 + 9 = 2x + 10$

6) $(y - 4)(y + 3) - (y - 6)^2 = y^2 - 4y + 3y - 12 - (y^2 - 12y + 36) = y^2 - y - 12 - y^2 + 12y - 36 = 11y - 48$

63. Постройте график функции:
1) y= 2;
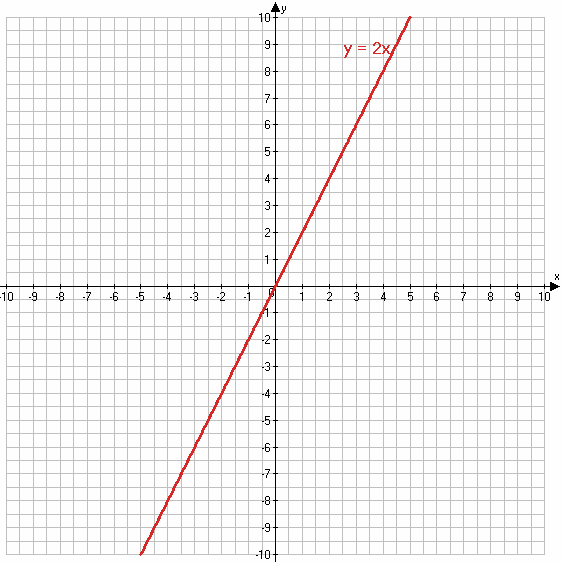
2) y = 2x;
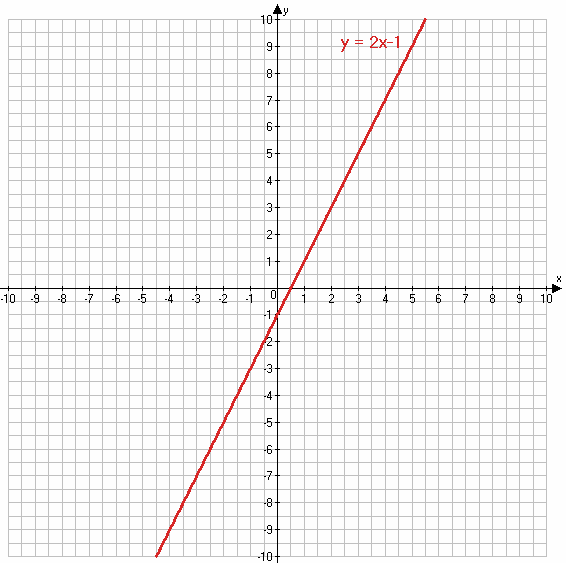
3) y = 2x − 1.

Решение:

1)


2)
х 2 3
у 4 6


3)
х 2 3
у 3 5