Ответы к странице 170
673. При каком значении a число 2 является корнем уравнения $x^2 - 0,5ax - 3a^2 = 0$?
Решение:
$x^2 - 0,5ax - 3a^2 = 0$
x = 2:
$2^2 - 0,5 * 2a - 3a^2 = 0$
$-3a^2 - a + 4 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * (-3) * 4 = 1 + 48 = 49 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{49}}{2 * (-3)} = \frac{1 + 7}{-6} = \frac{8}{-6} = -\frac{4}{3} = -1\frac{1}{3}$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{49}}{2 * (-3)} = \frac{1 - 7}{-6} = \frac{-6}{-6} = 1$
Ответ: при $a = -1\frac{1}{3}$ и a = 1
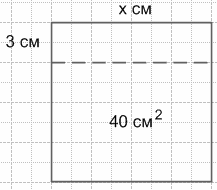
674. От квадратного листа картона отрезали полоску в форме прямоугольника шириной 3 см и длиной, равной стороне квадрата. Площадь оставшейся части листа составляет 40 $см^2$. Какой была длина стороны квадратного листа картона?
Решение:
Пусть x (см) − сторона квадрата, тогда:
$x^2 (см^2)$ − площадь квадрата;
$3x (см^2)$ − площадь отрезанной полоски.
Так как, площадь оставшейся части листа составляет 40 $см^2$, можно составить уравнение:
$x^2 - 3x = 40$
$x^2 - 3x - 40 = 0$
$D = b^2 - 4ac = (-3)^2 - 4 * 1 * (-40) = 9 + 160 = 169 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{3 + \sqrt{169}}{2 * 1} = \frac{3 + 13}{2} = \frac{16}{2} = 8$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{3 - \sqrt{169}}{2 * 1} = \frac{3 - 13}{2} = \frac{-10}{2} = -5$ − не удовлетворяет условию задачи, так как сторона квадрата не может быть отрицательной.
Тогда:
x = 8 (см) − сторона квадрата.
Ответ: 8 см
675. От прямоугольного листа бумаги, длина которого равна 18 см, отрезали квадрат, сторона которого равна ширине листа. Площадь оставшейся части прямоугольника составляет 72 $см^2$. Какой была ширина листа бумаги?
Решение:
Пусть x (см) − ширина прямоугольника, тогда:
$18x (см^2)$ − площадь прямоугольника;
$x^2 (см^2)$ − площадь отрезанного квадрата.
Так как, площадь оставшейся части прямоугольника составляет 72 $см^2$, можно составить уравнение:
$18x - x^2 = 72$
$-x^2 + 18x - 72 = 0$
$D = b^2 - 4ac = 18^2 - 4 * (-1) * (-72) = 324 - 288 = 36 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-18 + \sqrt{36}}{2 * (-1)} = \frac{-18 + 6}{-2} = \frac{-12}{-2} = 6$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-18 - \sqrt{36}}{2 * (-1)} = \frac{-18 - 6}{-2} = \frac{-24}{-2} = 12$
Получается, что сторона листа бумаги может быть либо 6 см, либо 12 см.
Ответ: 6 см или 12 см
676. Найдите катеты прямоугольного треугольника, если один из них на 14 см меньше другого, а гипотенуза равна 34 см.
Решение:
Пусть x (см) − длина меньшего катета, тогда:
x + 14 (см) − длина большего катета.
Так как, согласно теореме Пифагора: сумма квадратов длин катетов равна квадрату длины гипотенузы, можно составить уравнение:
$x^2 + (x + 14)^2 = 34^2$
$x^2 + x^2 + 28x + 196 = 1156$
$2x^2 + 28x + 196 - 1156 = 0$
$2x^2 + 28x - 960 = 0$ |: 2
$x^2 + 14x - 480 = 0$
$D = b^2 - 4ac = 14^2 - 4 * 1 * (-480) = 196 + 1920 = 2116 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-14 + \sqrt{2116}}{2 * 1} = \frac{-14 + 46}{2} = \frac{32}{2} = 16$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-14 - \sqrt{2116}}{2 * 1} = \frac{-14 - 46}{2} = \frac{-60}{2} = -30$ − не удовлетворяет условию задачи, так как длина катета не может быть отрицательной.
Тогда:
x = 16 (см) − длина меньшего катета, тогда:
x + 14 = 16 + 14 = 30 (см) − длина большего катета.
Ответ: 16 см и 30 см
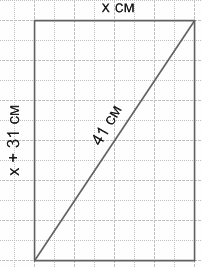
677. Найдите стороны прямоугольника, если их разность равна 31 см, а диагональ прямоугольника равна 41 см.
Решение:
Пусть x (см) − ширина прямоугольника, тогда:
x + 31 (см) − длина прямоугольника.
Так как, согласно теореме Пифагора: сумма квадратов длин катетов равна квадрату длины гипотенузы, можно составить уравнение:
$x^2 + (x + 31)^2 = 41^2$
$x^2 + x^2 + 62x + 961 = 1681$
$2x^2 + 62x + 961 - 1681 = 0$
$2x^2 + 62x - 720 = 0$ |: 2
$x^2 + 31x - 360 = 0$
$D = b^2 - 4ac = 31^2 - 4 * 1 * (-360) = 961 + 1440 = 2401 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-31 + \sqrt{2401}}{2 * 1} = \frac{-31 + 49}{2} = \frac{18}{2} = 9$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-31 - \sqrt{2401}}{2 * 1} = \frac{-31 - 49}{2} = \frac{-80}{2} = -40$ − не удовлетворяет условию задачи, так как ширина прямоугольника не может быть отрицательной.
Тогда:
x = 9 (см) − ширина прямоугольника, тогда:
x + 31 = 9 + 31 = 40 (см) − длина прямоугольника.
Ответ: 9 см и 40 см
678. Найдите три последовательных нечетных натуральных числа, если квадрат первого из них на 33 больше, чем удвоенная сумма второго и третьего.
Решение:
Пусть 2n − 1 − первое из трех последовательных нечетных натуральных числа, тогда:
2n + 1 − второе число;
2n + 3 − третье число.
Так как, квадрат первого из число на 33 больше, чем удвоенная сумма второго и третьего, можно составить уравнение:
$(2n - 1)^2 - 33 = 2(2n + 1 + 2n + 3)$
$4n^2 - 4n + 1 - 33 = 2(4n + 4)$
$4n^2 - 4n - 32 = 8n + 8$
$4n^2 - 4n - 8n - 32 - 8 = 0$
$4n^2 - 12n - 40 = 0$ |: 4
$n^2 - 3n - 10 = 0$
$D = b^2 - 4ac = (-3)^2 - 4 * 1 * (-10) = 9 + 40 = 49 > 0$
$n_1 = \frac{-b + \sqrt{D}}{2a} = \frac{3 + \sqrt{49}}{2 * 1} = \frac{3 + 7}{2} = \frac{10}{2} = 5$
$n_2 = \frac{-b - \sqrt{D}}{2a} = \frac{3 - \sqrt{49}}{2 * 1} = \frac{3 - 7}{2} = \frac{-4}{2} = -2$ − не удовлетворяет условию задачи, так как не является натуральным числом.
Тогда при n = 5:
2n − 1 = 2 * 5 − 1 = 10 − 1 = 9 − первое число;
2n + 1 = 2 * 5 + 1 = 10 + 1 = 11 − второе число;
2n + 3 = 2 * 5 + 3 = 10 + 3 = 13 − третье число.
Ответ: 9, 11 и 13.
679. Найдите четыре последовательных четных натуральных числа, если сумма первого и третьего чисел в 5 раз меньше, чем произведение второго и четвертого чисел.
Решение:
Пусть 2n − первое из четырех последовательных четных натуральных чисел, тогда:
2n + 2 − второе число;
2n + 4 − третье число;
2n + 6 − четвертое число.
Так как, сумма первого и третьего чисел в 5 раз меньше, чем произведение второго и четвертого чисел, можно составить уравнение:
5(2n + 2n + 4) = (2n + 2)(2n + 6)
$5(4n + 4) = 4n^2 + 4n + 12n + 12$
$20n + 20 = 4n^2 + 16n + 12$
$20n + 20 - 4n^2 - 16n - 12 = 0$
$-4n^2 + 4n + 8 = 0$ |: (−4)
$n^2 - n - 2 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 1 * (-2) = 1 + 8 = 9 > 0$
$n_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{9}}{2 * 1} = \frac{1 + 3}{2} = \frac{4}{2} = 2$
$n_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{9}}{2 * 1} = \frac{1 - 3}{2} = \frac{-2}{2} = -1$ − не удовлетворяет условию задачи, так как не является натуральным числом.
Тогда при n = 2:
2n = 2 * 2 = 4 − первое число;
2n + 2 = 2 * 2 + 2 = 4 + 2 = 6 − второе число;
2n + 4 = 2 * 2 + 4 = 4 + 4 = 8 − третье число;
2n + 6 = 2 * 2 + 6 = 4 + 6 = 10 − четвертое число.
Ответ: 4, 6, 8, 10.
680. Докажите, что если старший коэффициент и свободный член квадратного уравнения имеют разные знаки, то уравнение имеет два корня.
Решение:
$ax^2 + bx + c = 0$
Уравнение имеет два корня, если его дискриминант больше нуля.
Докажем, что:
$D = b^2 - 4ac > 0$, если a и c имеют разные знаки.
$b^2 ≥ 0$ − так как является квадратом числа.
если a и c имеют разные знаки, то их произведение будет отрицательным, зато произведение −4ac будет положительным.
Получается, что $b^2 ≥ 0$ и −4ac > 0, значит и $D = b^2 - 4ac > 0$, а значит уравнение имеет 2 корня.
681. (Старинная индийская задача.)
На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько было обезьянок,
Ты скажи мне, в этой стае?
Решение:
Пусть x (обезьян) − было всего, тогда:
$(\frac{1}{8}x)^2$ − резвилась в роще.
Зная, что оставшиеся 12 обезьян прыгали по лианам, можно составить уравнение:
$x - (\frac{1}{8}x)^2 = 12$
$-\frac{1}{64}x^2 + x - 12 = 0$ |(−64)
$x^2 - 64x + 768 = 0$
$D = b^2 - 4ac = (-64)^2 - 4 * 1 * 768 = 4096 - 3072 = 1024 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{64 + \sqrt{1024}}{2 * 1} = \frac{64 + 32}{2} = \frac{96}{2} = 48$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{64 - \sqrt{1024}}{2 * 1} = \frac{64 - 32}{2} = \frac{32}{2} = 16$
Ответ: было либо 16, либо 48 обезьян.
682. В футбольном турнире было сыграно 36 матчей. Сколько команд участвовало в турнире, если каждая команда сыграла по одному разу с каждой из остальных команд?
Решение:
Пусть x (команд) − участвовало в турнире, тогда:
x − 1 (матч) − сыграла каждая из команд;
так как в одном матче участвует сразу две команды, то:
$\frac{1}{2}x(x - 1)$ (матчей) − было сыграно всего.
Зная, что в футбольном турнире было сыграно всего 36 матчей, можно составить уравнение:
$\frac{1}{2}x(x - 1) = 36$
$\frac{1}{2}x^2 - \frac{1}{2}x = 36$ |* 2
$x^2 - x = 72$
$x^2 - x - 72 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 1 * (-72) = 1 + 288 = 289 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{289}}{2 * 1} = \frac{1 + 17}{2} = \frac{18}{2} = 9$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{289}}{2 * 1} = \frac{1 - 17}{2} = \frac{-16}{2} = -8$ − не удовлетворяет условию задачи, так как количество команд не может быть отрицательным.
Ответ: 9 команд
683. Сколько сторон у многоугольника, если в нем можно провести 90 диагоналей?
Решение:
Пусть x (сторон) − многоугольника, тогда:
(x − 3) диагонали можно провести в многоугольники из каждой вершины;
так как диагональ соединяет сразу две вершины, то:
$\frac{1}{2}x(x - 3)$ (диагоналей) всего можно провести в многоугольнике.
Зная, что всего в многоугольнике можно провести 90 диагоналей, составим уравнение:
$\frac{1}{2}x(x - 3) = 90$ |* 2
x(x − 3) = 180
$x^2 - 3x - 180 = 0$
$D = b^2 - 4ac = (-3)^2 - 4 * 1 * (-180) = 9 + 720 = 729 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{3 + \sqrt{729}}{2 * 1} = \frac{3 + 27}{2} = \frac{30}{2} = 15$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{3 - \sqrt{729}}{2 * 1} = \frac{3 - 27}{2} = \frac{-24}{2} = -12$ − не удовлетворяет условию задачи, так как количество сторон не может быть отрицательным.
Ответ: 15 сторон
684. Решите уравнение:
1) $|x^2 + 7x - 4| = 4$;
2) $5x^2 - 8|x| + 3 = 0$;
3) $x|x| + 6x - 5 = 0$;
4) $x^2 + \frac{4x^2}{|x|} - 12 = 0$;
5) $x^2 - 8\sqrt{x^2} + 15 = 0$;
6) $x^2 + 4\sqrt{x^2} - 12 = 0$.
Решение:
1) $|x^2 + 7x - 4| = 4$
а)
$x^2 + 7x - 4 = 4$
$x^2 + 7x - 4 - 4 = 0$
$x^2 + 7x - 8 = 0$
$D = b^2 - 4ac = 7^2 - 4 * 1 * (-8) = 49 + 32 = 81 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-7 + \sqrt{81}}{2 * 1} = \frac{-7 + 9}{2} = \frac{2}{2} = 1$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-7 - \sqrt{81}}{2 * 1} = \frac{-7 - 9}{2} = \frac{-16}{2} = -8$
б)
$x^2 + 7x - 4 = -4$
$x^2 + 7x - 4 + 4 = 0$
$x^2 + 7x = 0$
x(x + 7) = 0
x = 0
или
x + 7 = 0
x = −7
Ответ: −8; −7; 0; 1.
2) $5x^2 - 8|x| + 3 = 0$
а) x ≥ 0
$5x^2 - 8x + 3 = 0$
$D = b^2 - 4ac = (-8)^2 - 4 * 5 * 3 = 64 - 60 = 4 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{8 + \sqrt{4}}{2 * 5} = \frac{8 + 2}{10} = \frac{10}{10} = 1$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{8 - \sqrt{4}}{2 * 5} = \frac{8 - 2}{10} = \frac{6}{10} = 0,6$
б) x < 0
$5x^2 + 8x + 3 = 0$
$D = b^2 - 4ac = 8^2 - 4 * 5 * 3 = 64 - 60 = 4 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-8 + \sqrt{4}}{2 * 5} = \frac{-8 + 2}{10} = \frac{-6}{10} = -0,6$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-8 - \sqrt{4}}{2 * 5} = \frac{-8 - 2}{10} = \frac{-10}{10} = -1$
Ответ: −1; −0,6; 0,6; 1.
3) $x|x| + 6x - 5 = 0$
а) x ≥ 0
$x * x + 6x - 5 = 0$
$x^2 + 6x - 5 = 0$
$D = b^2 - 4ac = 6^2 - 4 * 1 * (-5) = 36 + 20 = 56 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-6 + \sqrt{56}}{2 * 1} = \frac{-6 + \sqrt{4 * 14}}{2} = \frac{-6 + 2\sqrt{14}}{2} = \frac{2(-3 + \sqrt{14})}{2} = -3 + \sqrt{14}$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-6 - \sqrt{56}}{2 * 1} = \frac{-6 - \sqrt{4 * 14}}{2} = \frac{-6 - 2\sqrt{14}}{2} = \frac{2(-3 - \sqrt{14})}{2} = -3 - \sqrt{14} < 0$ − не удовлетворяет условию, так как x ≥ 0.
б) x < 0
$x * (-x) + 6x - 5 = 0$
$-x^2 + 6x - 5 = 0$
$D = b^2 - 4ac = 6^2 - 4 * (-1) * (-5) = 36 - 20 = 16 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-6 + \sqrt{16}}{2 * (-1)} = \frac{-6 + 4}{-2} = \frac{-2}{-2} = 1 > 0$ − не удовлетворяет условию, так как x < 0.
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-6 - \sqrt{16}}{2 * (-1)} = \frac{-6 - 4}{-2} = \frac{-10}{-2} = 5 > 0$ − не удовлетворяет условию, так как x < 0.
Ответ: $-3 + \sqrt{14}$
4) $x^2 + \frac{4x^2}{|x|} - 12 = 0$
а) x > 0
$x^2 + \frac{4x^2}{x} - 12 = 0$
$x^2 + 4x - 12 = 0$
$D = b^2 - 4ac = 4^2 - 4 * 1 * (-12) = 16 + 48 = 64 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-4 + \sqrt{64}}{2 * 1} = \frac{-4 + 8}{2} = \frac{4}{2} = 2$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-4 - \sqrt{64}}{2 * 1} = \frac{-4 - 8}{2} = \frac{-12}{2} = -6 < 0$ − не удовлетворяет условию, так как x > 0.
б) x < 0
$x^2 + \frac{4x^2}{-x} - 12 = 0$
$x^2 - 4x - 12 = 0$
$D = b^2 - 4ac = (-4)^2 - 4 * 1 * (-12) = 16 + 48 = 64 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{4 + \sqrt{64}}{2 * 1} = \frac{4 + 8}{2} = \frac{12}{2} = 6 > 0$ − не удовлетворяет условию, так как x < 0.
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{4 - \sqrt{64}}{2 * 1} = \frac{4 - 8}{2} = \frac{-4}{2} = -2 < 0$
Ответ: −2; 2.
5) $x^2 - 8\sqrt{x^2} + 15 = 0$
$x^2 - 8|x| + 15 = 0$
а) x ≥ 0
$x^2 - 8x + 15 = 0$
$D = b^2 - 4ac = (-8)^2 - 4 * 1 * 15 = 64 - 60 = 4 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{8 + \sqrt{4}}{2 * 1} = \frac{8 + 2}{2} = \frac{10}{2} = 5$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{8 - \sqrt{4}}{2 * 1} = \frac{8 - 2}{2} = \frac{6}{2} = 3$
б) x < 0
$x^2 + 8x + 15 = 0$
$D = b^2 - 4ac = 8^2 - 4 * 1 * 15 = 64 - 60 = 4 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-8 + \sqrt{4}}{2 * 1} = \frac{-8 + 2}{2} = \frac{-6}{2} = -3$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-8 - \sqrt{4}}{2 * 1} = \frac{-8 - 2}{2} = \frac{-10}{2} = -5$
Ответ: −5; −3; 3; 5.
6) $x^2 + 4\sqrt{x^2} - 12 = 0$
$x^2 + 4|x| - 12 = 0$
а) x ≥ 0
$x^2 + 4x - 12 = 0$
$D = b^2 - 4ac = 4^2 - 4 * 1 * (-12) = 16 + 48 = 64 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-4 + \sqrt{64}}{2 * 1} = \frac{-4 + 8}{2} = \frac{4}{2} = 2$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-4 - \sqrt{64}}{2 * 1} = \frac{-4 - 8}{2} = \frac{-12}{2} = -6 < 0$ − не удовлетворяет условию, так как x ≥ 0.
б) x < 0
$x^2 - 4x - 12 = 0$
$D = b^2 - 4ac = (-4)^2 - 4 * 1 * (-12) = 16 + 48 = 64 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{4 + \sqrt{64}}{2 * 1} = \frac{4 + 8}{2} = \frac{12}{2} = 6 > 0$ − не удовлетворяет условию, так как x < 0.
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{4 - \sqrt{64}}{2 * 1} = \frac{4 - 8}{2} = \frac{-4}{2} = -2 < 0$
Ответ: −2; 2.