Ответы к странице 186
760. При каком значении a разложение на линейные множители трехчлена:
1) $2x^2 - 7x + a$ содержит множитель (x − 4);
2) $4x^2 - ax + 6$ содержит множитель (2x + 1).
Решение:
1) $2x^2 - 7x + a = 2(x - 4)(x - x_2)$
$x_1 = 4$
$x_1 + x_2 = -\frac{b}{a} = -\frac{-7}{2} = 3,5$
$4 + x_2 = 3,5$
$x_2 = 3,5 - 4$
$x_2 = -0,5$
$x_1x_2 = \frac{c}{a} = \frac{a}{2}$
$\frac{a}{2} = 4 * (-0,5)$
$\frac{a}{2} = -2$
a = −4
Ответ: при a = −4
2) $4x^2 - ax + 6 = 4(x - x_1)(x - x_2) = 2 * 2(x - x_1)(x - x_2) = 2 * (2x - 2x_1) * (x - x_2)$
$2x - 2x_1 = 2x + 1$
$-2x_1 = 1$
$x_1 = -0,5$
$x_1x_2 = \frac{c}{a} = \frac{6}{4} = \frac{3}{2} = 1,5$
$-0,5 * x_2 = 1,5$
$x_2 = -\frac{1,5}{0,5}$
$x_2 = -\frac{15}{5}$
$x_2 = -3$
$x_1 + x_2 = -\frac{b}{a} = -\frac{-a}{4} = \frac{a}{4}$
$\frac{a}{4} = -0,5 + (-3)$
$\frac{a}{4} = -3,5$
a = −3,5 * 4
a = −14
Ответ: при a = −14
761. Упростите выражение:
1) $\frac{9a^2 - 4}{2a^2 - 5a + 2} * \frac{a - 2}{3a + 2} + \frac{a - 1}{1 - 2a}$;
2) $\frac{b - 4}{b^3 - b} : (\frac{b - 1}{2b^2 + 3b + 1} - \frac{1}{b^2 - 1})$;
3) $(\frac{c + 2}{c^2 - c - 6} - \frac{2c}{c^2 - 6c + 9}) : \frac{с^2 + 3c}{(2c - 6)^2}$;
4) $(\frac{3}{m - 4} + \frac{2m}{m + 1} + \frac{4m - 6}{m^2 - 3m - 4}) * \frac{4m - 16}{2m - 3}$.
Решение:
1) $\frac{9a^2 - 4}{2a^2 - 5a + 2} * \frac{a - 2}{3a + 2} + \frac{a - 1}{1 - 2a}$
$2a^2 - 5a + 2 = 0$
$D = b^2 - 4ac = (-5)^2 - 4 * 2 * 2 = 25 - 16 = 9 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{5 + \sqrt{9}}{2 * 2} = \frac{5 + 3}{4} = \frac{8}{4} = 2$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{5 - \sqrt{9}}{2 * 2} = \frac{5 - 3}{4} = \frac{2}{4} = 0,5$
$2a^2 - 5a + 2 = 2(a - 2)(a - 0,5) = (a - 2)(2a - 1)$
тогда:
$\frac{9a^2 - 4}{(a - 2)(2a - 1)} * \frac{a - 2}{3a + 2} + \frac{a - 1}{1 - 2a} = \frac{(3a - 2)(3a + 2)}{2a - 1} * \frac{1}{3a + 2} + \frac{a - 1}{1 - 2a} = \frac{3a - 2}{2a - 1} + \frac{a - 1}{1 - 2a} = \frac{3a - 2}{2a - 1} - \frac{a - 1}{2a - 1} = \frac{3a - 2 - (a - 1)}{2a - 1} = \frac{3a - 2 - a + 1}{2a - 1} = \frac{2a - 1}{2a - 1} = 1$
2) $\frac{b - 4}{b^3 - b} : (\frac{b - 1}{2b^2 + 3b + 1} - \frac{1}{b^2 - 1})$
$2b^2 + 3b + 1 = 0$
$D = b^2 - 4ac = 3^2 - 4 * 2 * 1 = 9 - 8 = 1 > 0$
$b_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-3 + \sqrt{1}}{2 * 2} = \frac{-3 + 1}{4} = \frac{-2}{4} = -0,5$
$b_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-3 - \sqrt{1}}{2 * 2} = \frac{-3 - 1}{4} = \frac{-4}{4} = -1$
$2b^2 + 3b + 1 = 2(b - (-0,5))(b - (-1)) = 2(b + 0,5)(b + 1) = (2b + 1)(b + 1)$
тогда:
$\frac{b - 4}{b^3 - b} : (\frac{b - 1}{(2b + 1)(b + 1)} - \frac{1}{b^2 - 1}) = \frac{b - 4}{b(b^2 - 1)} : (\frac{b - 1}{(2b + 1)(b + 1)} - \frac{1}{(b - 1)(b + 1)}) = \frac{b - 4}{b(b^2 - 1)} : \frac{(b - 1)^2 - (2b + 1)}{(2b + 1)(b - 1)(b + 1)} = \frac{b - 4}{b(b^2 - 1)} : \frac{b^2 - 2b + 1 - 2b - 1}{(2b + 1)(b^2 - 1)} = \frac{b - 4}{b(b^2 - 1)} : \frac{b^2 - 4b}{(2b + 1)(b^2 - 1)} = \frac{b - 4}{b(b^2 - 1)} : \frac{b(b - 4)}{(2b + 1)(b^2 - 1)} = \frac{b - 4}{b(b^2 - 1)} * \frac{(2b + 1)(b^2 - 1)}{b(b - 4)} = \frac{1}{b} * \frac{2b + 1}{b} = \frac{2b + 1}{b^2}$
3) $(\frac{c + 2}{c^2 - c - 6} - \frac{2c}{c^2 - 6c + 9}) : \frac{с^2 + 3c}{(2c - 6)^2}$
$c^2 - c - 6 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 1 * (-6) = 1 + 24 = 25 > 0$
$c_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{25}}{2 * 1} = \frac{1 + 5}{2} = \frac{6}{2} = 3$
$c_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{25}}{2 * 1} = \frac{1 - 5}{2} = \frac{-4}{2} = -2$
$c^2 - c - 6 = (c - 3)(c - (-2)) = (c - 3)(c + 2)$
тогда:
$(\frac{c + 2}{(c - 3)(c + 2)} - \frac{2c}{c^2 - 6c + 9}) : \frac{с^2 + 3c}{(2c - 6)^2} = (\frac{1}{c - 3} - \frac{2c}{(c - 3)^2}) : \frac{с^2 + 3c}{(2c - 6)^2} = \frac{c - 3 - 2c}{(c - 3)^2} : \frac{c(c + 3)}{(2(c - 3))^2} = \frac{-c - 3}{(c - 3)^2} * \frac{4(c - 3)^2}{c(c + 3)} = \frac{-(c + 3)}{1} * \frac{4}{c(c + 3)} = -\frac{4}{c}$
4) $(\frac{3}{m - 4} + \frac{2m}{m + 1} + \frac{4m - 6}{m^2 - 3m - 4}) * \frac{4m - 16}{2m - 3}$
$m^2 - 3m - 4 = 0$
$D = b^2 - 4ac = (-3)^2 - 4 * 1 * (-4) = 9 + 16 = 25 > 0$
$m_1 = \frac{-b + \sqrt{D}}{2a} = \frac{3 + \sqrt{25}}{2 * 1} = \frac{3 + 5}{2} = \frac{8}{2} = 4$
$m_2 = \frac{-b - \sqrt{D}}{2a} = \frac{3 - \sqrt{25}}{2 * 1} = \frac{3 - 5}{2} = \frac{-2}{2} = -1$
$m^2 - 3m - 4 = (m - 4)(m - (-1)) = (m - 4)(m + 1)$
тогда:
$(\frac{3}{m - 4} + \frac{2m}{m + 1} + \frac{4m - 6}{(m - 4)(m + 1)}) * \frac{4m - 16}{2m - 3} = \frac{3(m + 1) + 2m(m - 4) + 4m - 6}{(m - 4)(m + 1)} * \frac{4(m - 4)}{2m - 3} = \frac{3m + 3 + 2m^2 - 8m + 4m - 6}{m + 1} * \frac{4}{2m - 3} = \frac{2m^2 - m - 3}{m + 1} * \frac{4}{2m - 3}$
$2m^2 - m - 3 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 2 * (-3) = 1 + 24 = 25 > 0$
$m_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{25}}{2 * 2} = \frac{1 + 5}{4} = \frac{6}{4} = 1,5$
$m_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{25}}{2 * 2} = \frac{1 - 5}{4} = \frac{-4}{4} = -1$
$2m^2 - m - 3 = 2(m - 1,5)(m - (-1)) = (2m - 3)(m + 1)$
тогда:
$\frac{(2m - 3)(m + 1)}{m + 1} * \frac{4}{2m - 3} = 4$
762. Докажите, что при всех допустимых значениях a значение выражения не зависит от значения переменной:
1) $\frac{25a^2 - 36}{10a^2 - 9a + 2} : \frac{5a + 6}{5a - 2} + \frac{9a - 8}{1 - 2a}$;
2) $(\frac{2a}{a + 3} + \frac{1}{a - 1} - \frac{4}{a^2 + 2a - 3}) : \frac{2a + 1}{a + 3}$.
Решение:
1) $\frac{25a^2 - 36}{10a^2 - 9a + 2} : \frac{5a + 6}{5a - 2} + \frac{9a - 8}{1 - 2a}$
$10a^2 - 9a + 2 = 0$
$D = b^2 - 4ac = (-9)^2 - 4 * 10 * 2 = 81 - 80 = 1 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{9 + \sqrt{1}}{2 * 10} = \frac{9 + 1}{20} = \frac{10}{20} = 0,5$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{9 - \sqrt{1}}{2 * 10} = \frac{9 - 1}{20} = \frac{8}{20} = 0,4$
$10a^2 - 9a + 2 = 10(a - 0,5)(a - 0,4) = 2(a - 0,5) * 5(a - 0,4) = (2a - 1)(5a - 2)$
тогда:
$\frac{25a^2 - 36}{(2a - 1)(5a - 2)} : \frac{5a + 6}{5a - 2} + \frac{9a - 8}{1 - 2a} = \frac{(5a - 6)(5a + 6)}{(2a - 1)(5a - 2)} * \frac{5a - 2}{5a + 6} + \frac{9a - 8}{1 - 2a} = \frac{5a - 6}{2a - 1} + \frac{9a - 8}{1 - 2a} = \frac{5a - 6}{2a - 1} - \frac{9a - 8}{2a - 1} = \frac{5a - 6 - (9a - 8)}{2a - 1} = \frac{5a - 6 - 9a + 8}{2a - 1} = \frac{-4a + 2}{2a - 1} = \frac{-2(2a - 1)}{2a - 1} = -2$
2) $(\frac{2a}{a + 3} + \frac{1}{a - 1} - \frac{4}{a^2 + 2a - 3}) : \frac{2a + 1}{a + 3}$
$a^2 + 2a - 3 = 0$
$D = b^2 - 4ac = 2^2 - 4 * 1 * (-3) = 4 + 12 = 16 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-2 + \sqrt{16}}{2 * 1} = \frac{-2 + 4}{2} = \frac{2}{2} = 1$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-2 - \sqrt{16}}{2 * 1} = \frac{-2 - 4}{2} = \frac{-6}{2} = -3$
$a^2 + 2a - 3 = (a - 1)(a - (-3)) = (a - 1)(a + 3)$
тогда:
$(\frac{2a}{a + 3} + \frac{1}{a - 1} - \frac{4}{(a - 1)(a + 3)}) : \frac{2a + 1}{a + 3} = \frac{2a(a - 1) + a + 3 - 4}{(a - 1)(a + 3)} * \frac{a + 3}{2a + 1} = \frac{2a^2 - 2a + a - 1}{a - 1} * \frac{1}{2a + 1} = \frac{2a^2 - a - 1}{a - 1} * \frac{1}{2a + 1}$
$2a^2 - a - 1 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 2 * (-1) = 1 + 8 = 9 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{9}}{2 * 2} = \frac{1 + 3}{4} = \frac{4}{4} = 1$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{9}}{2 * 2} = \frac{1 - 3}{4} = \frac{-2}{4} = -0,5$
$2a^2 - a - 1 = 2(a - 1)(a - (-0,5)) = 2(a - 1)(a + 0,5) = (a - 1)(2a + 1)$
тогда:
$\frac{(a - 1)(2a + 1)}{a - 1} * \frac{1}{2a + 1} = 1$
763. Постройте график функции:
1) $\frac{x^2 - 6x + 5}{x - 1}$;
2) $\frac{3x^2 - 10x + 3}{x - 3} - \frac{x^2 - 4}{x + 2}$.
Решение:
1) $\frac{x^2 - 6x + 5}{x - 1}$
x − 1 ≠ 0
x ≠ 1
$x^2 - 6x + 5 = 0$
$D = b^2 - 4ac = (-6)^2 - 4 * 1 * 5 = 36 + 20 = 16 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{6 + \sqrt{16}}{2 * 1} = \frac{6 + 4}{2} = \frac{10}{2} = 5$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{6 - \sqrt{16}}{2 * 1} = \frac{6 - 4}{2} = \frac{2}{2} = 1$
$x^2 - 6x + 5 = (x - 5)(x - 1)$
тогда:
$\frac{(x - 5)(x - 1)}{x - 1} = x - 5$
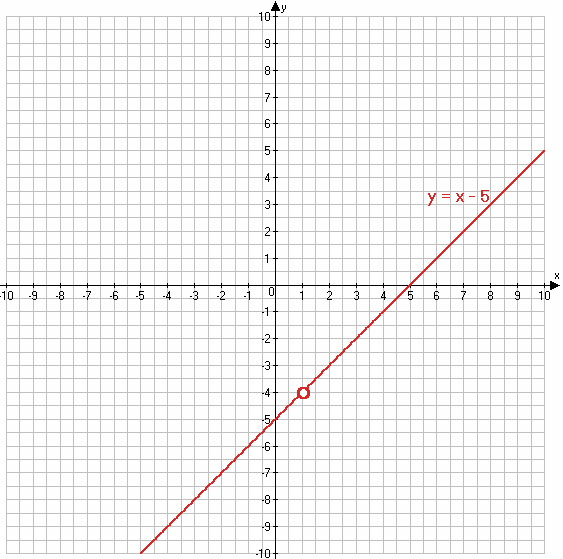
y = x − 5 при x ≠ 1
х 0 2
у -5 -3
2) $\frac{3x^2 - 10x + 3}{x - 3} - \frac{x^2 - 4}{x + 2}$
x − 3 ≠ 0
x ≠ 3
и
x + 2 ≠ 0
x ≠ −2
$3x^2 - 10x + 3 = 0$
$D = b^2 - 4ac = (-10)^2 - 4 * 3 * 3 = 100 - 36 = 64 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{10 + \sqrt{64}}{2 * 3} = \frac{10 + 8}{6} = \frac{18}{6} = 3$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{10 - \sqrt{64}}{2 * 3} = \frac{10 - 8}{6} = \frac{2}{6} = \frac{1}{3}$
$3x^2 - 10x + 3 = 3(x - 3)(x - \frac{1}{3}) = (x - 3)(3x - 1)$
тогда:
$\frac{(x - 3)(3x - 1)}{x - 3} - \frac{x^2 - 4}{x + 2} = 3x - 1 - \frac{(x - 2)(x + 2)}{x + 2} = 3x - 1 - (x - 2) = 3x - 1 - x + 2 = 2x + 1$
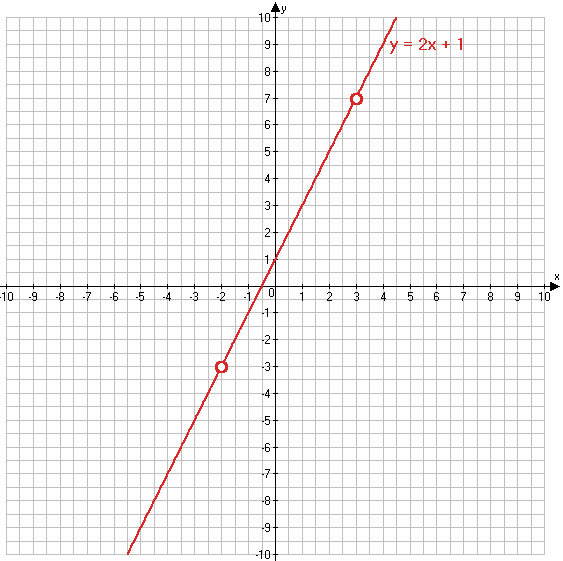
y = 2x + 1 при x ≠ −2 и x ≠ 3
х 0 1
у 1 3
764. Постройте график функции:
1) $\frac{x^2 - 2x - 8}{x - 4}$;
2) $\frac{x^2 - x - 2}{x + 1} - \frac{x^2 - x - 30}{x + 5}$.
Решение:
1) $\frac{x^2 - 2x - 8}{x - 4}$
x − 4 ≠ 0
x ≠ 4
$x^2 - 2x - 8 = 0$
$D = b^2 - 4ac = (-2)^2 - 4 * 1 * (-8) = 4 + 32 = 36 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{2 + \sqrt{36}}{2 * 1} = \frac{2 + 6}{2} = \frac{8}{2} = 4$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{2 - \sqrt{36}}{2 * 1} = \frac{2 - 6}{2} = \frac{-4}{2} = -2$
$x^2 - 2x - 8 = (x - 4)(x - (-2)) = (x - 4)(x + 2)$
тогда:
$\frac{(x - 4)(x + 2)}{x - 4} = x + 2$
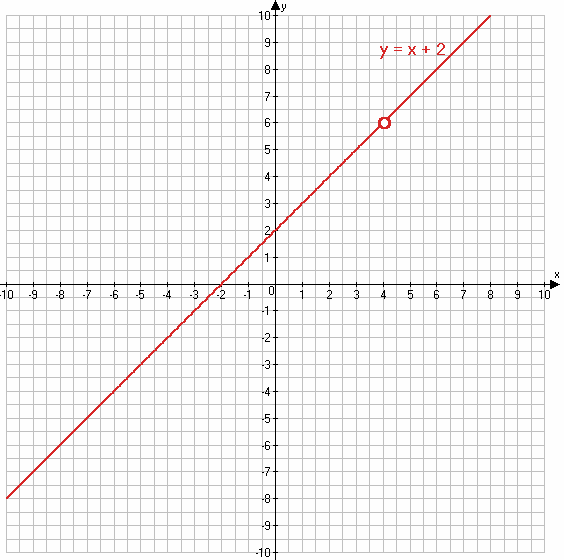
y = x + 2 при x ≠ 4
х 0 1
у 2 3
2) $\frac{x^2 - x - 2}{x + 1} - \frac{x^2 - x - 30}{x + 5}$
x + 1 ≠ 0
x ≠ −1
и
x + 5 ≠ 0
x ≠ −5
$x^2 - x - 2 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 1 * (-2) = 1 + 8 = 9 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{9}}{2 * 1} = \frac{1 + 3}{2} = \frac{4}{2} = 2$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{9}}{2 * 1} = \frac{1 - 3}{2} = \frac{-2}{2} = -1$
$x^2 - 2x - 8 = (x - 2)(x - (-1)) = (x - 2)(x + 1)$
$x^2 - x - 30 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 1 * (-30) = 1 + 120 = 121 > 0$
$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{121}}{2 * 1} = \frac{1 + 11}{2} = \frac{12}{2} = 6$
$x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{121}}{2 * 1} = \frac{1 - 11}{2} = \frac{-10}{2} = -5$
$x^2 - x - 30 = (x - 6)(x - (-5)) = (x - 6)(x + 5)$
тогда:
$\frac{(x - 2)(x + 1)}{x + 1} - \frac{(x - 6)(x + 5)}{x + 5} = x - 2 - (x - 6) = x - 2 - x + 6 = 4$
y = 4 при x ≠ −5 и x ≠ −1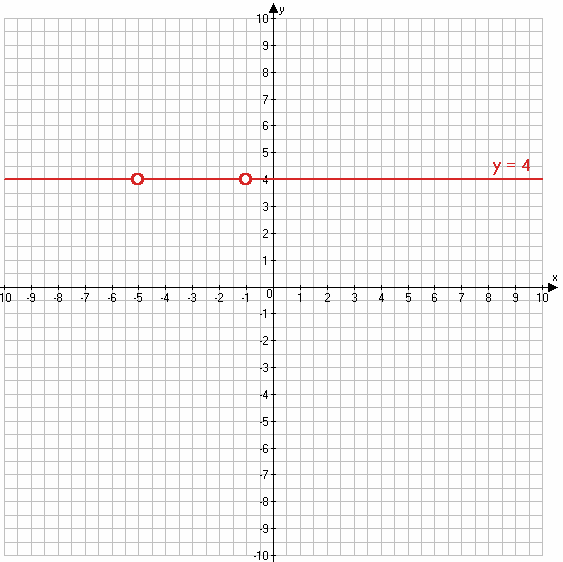
765. Разложите на множители многочлен:
1) $x^2 - 6xy + 5y^2$;
2) $a^2 + 5ab - 36b^2$;
3) $3m^2 - 8mn - 3n^2$;
4) $4x^2 - 5xy + y^2$.
Решение:
1) $x^2 - 6xy + 5y^2 = x^2 - xy - 5xy + 5y^2 = (x^2 - xy) - (5xy - 5y^2) = x(x - y) - 5y(x - y) = (x - y)(x - 5y)$
2) $a^2 + 5ab - 36b^2 = a^2 + 9ab - 4ab - 36b^2 = (a^2 + 9ab) - (4ab + 36b^2) = a(a + 9b) - 4b(a + 9b) = (a + 9b)(a - 4b)$
3) $3m^2 - 8mn - 3n^2 = 3m^2 + mn - 9mn - 3n^2 = (3m^2 + mn) - (9mn + 3n^2) = m(3m + n) - 3n(3m + n) = (3m + n)(m - 3n)$
4) $4x^2 - 5xy + y^2 = 4x^2 - xy - 4xy + y^2 = (4x^2 - xy) - (4xy - y^2) = x(4x - y) - y(4x - y) = (4x - y)(x - y)$
766. Разложите на множители многочлен:
1) $a^2 - 14ab + 40b^2$;
2) $12b^2 + bc - 6c^2$.
Решение:
1) $a^2 - 14ab + 40b^2 = a^2 - 4ab - 10ab + 40b^2 = (a^2 - 4ab) - (10ab - 40b^2) = a(a - 4b) - 10b(a - 4b) = (a - 4b)(a - 10b)$
2) $12b^2 + bc - 6c^2 = 12b^2 - 8bc + 9bc - 6c^2 = (12b^2 - 8bc) + (9bc - 6c^2) = 4b(3b - 2c) + 3c(3b - 2c) = (3b - 2c)(4b + 3c)$
767. Для каждого значения a решите уравнение:
1) $(a^2 - a - 6)x = a^2 - 9$;
2) $(a^2 - 8a + 7)x = 2a^2 - 13a - 7$.
Решение:
1) $(a^2 - a - 6)x = a^2 - 9$
$a^2 - a - 6 = 0$
$D = b^2 - 4ac = (-1)^2 - 4 * 1 * (-6) = 1 + 24 = 25 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{1 + \sqrt{25}}{2 * 1} = \frac{1 + 5}{2} = \frac{6}{2} = 3$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{1 - \sqrt{25}}{2 * 1} = \frac{1 - 5}{2} = \frac{-4}{2} = -2$
$a^2 - a - 6 = (a - 3)(a - (-2)) = (a - 3)(a + 2)$
тогда:
$(a - 3)(a + 2)x = a^2 - 9$
при a = 3:
$(3 - 3)(3 + 2)x = 3^2 - 9$
0 * 5x = 9 − 9
0 = 0
x − любое число.
при a = −2:
$(-2 - 3)(-2 + 2)x = (-2)^2 - 9$
−5 * 0x = 4 − 9
0x = −5
0 ≠ −5 − нет решений
при a ≠ −2 и a ≠ 3:
$x = \frac{(a - 3)(a + 3)}{(a - 3)(a + 2)} = \frac{a + 3}{a + 2}$
Ответ:
при a = 3: x − любое число;
при a = −2: нет решений;
при a ≠ −2 и a ≠ 3: $x = \frac{a + 3}{a + 2}$.
2) $(a^2 - 8a + 7)x = 2a^2 - 13a - 7$
$a^2 - 8a + 7 = 0$
$D = b^2 - 4ac = (-8)^2 - 4 * 1 * 7 = 64 - 28 = 36 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{8 + \sqrt{36}}{2 * 1} = \frac{8 + 6}{2} = \frac{14}{2} = 7$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{8 - \sqrt{36}}{2 * 1} = \frac{8 - 6}{2} = \frac{2}{2} = 1$
$a^2 - 8a + 7 = (a - 7)(a - 1)$
$2a^2 - 13a - 7 = 0$
$D = b^2 - 4ac = (-13)^2 - 4 * 2 * (-7) = 169 + 56 = 225 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{13 + \sqrt{225}}{2 * 2} = \frac{13 + 15}{4} = \frac{28}{4} = 7$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{13 - \sqrt{225}}{2 * 2} = \frac{13 - 15}{4} = \frac{-2}{4} = -0,5$
$2a^2 - 13a - 7 = 2(a - 7)(a - (-0,5)) = 2(a - 7)(a + 0,5) = (a - 7)(2a + 1)$
$2a^2 - 13a - 7 = (a - 7)(2a + 1)$
тогда:
$(a - 7)(a - 1)x = (a - 7)(2a + 1)$
при a = 7:
$(7 - 7)(7 - 1)x = (7 - 7)(2 * 7 + 1)$
$0 * 6x = 0 * 15$
0 = 0
x − любое число
при a = 1:
$(1 - 7)(1 - 1)x = (1 - 7)(2 * 1 + 1)$
$-6 * 0x = -6 * 3$
0 ≠ −18 − нет решений
при a = a ≠ 1 и a ≠ 7:
$x = \frac{(a - 7)(2a + 1)}{(a - 7)(a - 1)} = \frac{2a + 1}{a - 1}$
Ответ:
при a = 7: x − любое число;
при a = 1: нет решений;
при a ≠ 1 и a ≠ 7: $x = \frac{2a + 1}{a - 1}$.
768. Для каждого значения a решите уравнение $(a^2 + 7a - 8)x = a^2 + 16a + 64$.
Решение:
$(a^2 + 7a - 8)x = a^2 + 16a + 64$
$a^2 + 7a - 8 = 0$
$D = b^2 - 4ac = 7^2 - 4 * 1 * (-8) = 49 + 32 = 81 > 0$
$a_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-7 + \sqrt{81}}{2 * 1} = \frac{-7 + 9}{2} = \frac{2}{2} = 1$
$a_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-7 - \sqrt{81}}{2 * 1} = \frac{-7 - 9}{2} = \frac{-16}{2} = -8$
$a^2 + 7a - 8 = (a - 1)(a - (-8)) = (a - 1)(a + 8)$
тогда:
$(a - 1)(a + 8)x = (a + 8)^2$
при a = 1:
$(1 - 1)(1 + 8)x = (1 + 8)^2$
0 * 9x = 9^2
0 ≠ 81 − нет корней
при a = −8:
$(-8 - 1)(-8 + 8)x = (-8 + 8)^2$
−9 * 0x = 0
0 = 0
x − любое число
при a ≠ −8 и a ≠ 1:
$(a - 1)(a + 8)x = (a + 8)^2$
$x = \frac{(a + 8)^2}{(a - 1)(a + 8)} = \frac{a + 8}{a - 1}$
Ответ:
при a = 1: нет корней;
при a = −8: x − любое число;
при a ≠ −8 и a ≠ 1: $x = \frac{a + 8}{a - 1}$.
769. Сократите дробь:
1) $\frac{3 + \sqrt{3}}{2\sqrt{3}}$;
2) $\frac{5 - \sqrt{5}}{\sqrt{10} - 5\sqrt{2}}$;
3) $\frac{2 - \sqrt{6}}{\sqrt{6} - 3}$;
4) $\frac{4a - 2}{2\sqrt{a} + \sqrt{2}}$;
5) $\frac{9a - b^2}{9a + 6b\sqrt{a} + b^2}$;
6) $\frac{a\sqrt{a} - 8}{a + 2\sqrt{a} + 4}$.
Решение:
1) $\frac{3 + \sqrt{3}}{2\sqrt{3}} = \frac{(\sqrt{3})^2 + \sqrt{3}}{2\sqrt{3}} = \frac{\sqrt{3}(\sqrt{3} + 1)}{2\sqrt{3}} = \frac{\sqrt{3} + 1}{2}$
2) $\frac{5 - \sqrt{5}}{\sqrt{10} - 5\sqrt{2}} = \frac{(\sqrt{5})^2 - \sqrt{5}}{\sqrt{5 * 2} - 5\sqrt{2}} = \frac{\sqrt{5}(\sqrt{5} - 1)}{\sqrt{2} * \sqrt{5} - 5\sqrt{2}} = \frac{\sqrt{5}(\sqrt{5} - 1)}{\sqrt{2}(\sqrt{5} - 5)} = \frac{\sqrt{5}(\sqrt{5} - 1)}{\sqrt{2}(\sqrt{5} - (\sqrt{5})^2)} = \frac{\sqrt{5}(\sqrt{5} - 1)}{\sqrt{2} * \sqrt{5}(1 - \sqrt{5})} = -\frac{\sqrt{5} - 1}{\sqrt{2}(\sqrt{5} - 1)} = -\frac{1}{\sqrt{2}} = -\frac{1 * \sqrt{2}}{\sqrt{2} * \sqrt{2}} = -\frac{\sqrt{2}}{2}$
3) $\frac{2 - \sqrt{6}}{\sqrt{6} - 3} = \frac{(\sqrt{2})^2 - \sqrt{2} * \sqrt{3}}{\sqrt{2} * \sqrt{3} - (\sqrt{3})^2} = \frac{\sqrt{2}(\sqrt{2} - \sqrt{3})}{\sqrt{3}(\sqrt{2} - \sqrt{3})} = \frac{\sqrt{2}}{\sqrt{3}} = \frac{\sqrt{2} * \sqrt{3}}{\sqrt{3} * \sqrt{3}} = \frac{\sqrt{6}}{3}$
4) $\frac{4a - 2}{2\sqrt{a} + \sqrt{2}} = \frac{2(2a - 1)}{(\sqrt{2})^2 * \sqrt{a} + \sqrt{2}} = \frac{(\sqrt{2})^2((\sqrt{2a})^2 - 1^2)}{\sqrt{2}(\sqrt{2a} + 1)} = \frac{\sqrt{2}(\sqrt{2a} - 1)(\sqrt{2a} + 1)}{\sqrt{2a} + 1} = \sqrt{2}(\sqrt{2a} - 1)$
5) $\frac{9a - b^2}{9a + 6b\sqrt{a} + b^2} = \frac{(3\sqrt{a})^2 - b^2}{(3\sqrt{a})^2 + 2 * 3\sqrt{a} * b + b^2} = \frac{(3\sqrt{a} - b)(3\sqrt{a} + b)}{(3\sqrt{a} + b)^2} = \frac{3\sqrt{a} - b}{3\sqrt{a} + b}$
6) $\frac{a\sqrt{a} - 8}{a + 2\sqrt{a} + 4} = \frac{(\sqrt{a})^2 * \sqrt{a} - 2^3}{a + 2\sqrt{a} + 4} = \frac{(\sqrt{a})^3 - 2^3}{a + 2\sqrt{a} + 4} = \frac{(\sqrt{a} - 2)((\sqrt{a})^2 + 2\sqrt{a} + 2^2)}{a + 2\sqrt{a} + 4} = \frac{(\sqrt{a} - 2)(a + 2\sqrt{a} + 4)}{a + 2\sqrt{a} + 4} = \sqrt{a} - 2$