Задание №93

Черепаха развивает скорость до 0,8 км/ч, слон − до 40 км/ч, кенгуру − до 50 км/ч, заяц − русак − до 60 км/ч, страус − до 80 км/ч, антилопа гну − до 90 км/ч, гепард − до 120 км/ч. Рассчитайте время, за которое каждый из них преодолеет олимпийские дистанции 100, 200 и 400 м.

Решение

Дано:
$v_{1}$ = 0,8 км/ч;
$v_{2}$ = 40 км/ч;
$v_{3}$ = 50 км/ч;
$v_{4}$ = 60 км/ч;
$v_{5}$ = 80 км/ч;
$v_{6}$ = 90 км/ч;
$v_{7}$ = 120 км/ч;
$S_{А}$ = 100 м;
$S_{Б}$ = 200 м;
$S_{В}$ = 400 м.
Найти:
t − ?
СИ:
$S_{А}$ = 0,1 км;
$S_{Б}$ = 0,2 км;
$S_{В}$ = 0,4 км;
Решение:
$t_{1А} = \frac{0,1}{0,8}$ = 0,125 ч = 450 сек.
$t_{1Б} = \frac{0,2}{0,8}$ = 0,25 ч = 900 сек.
$t_{1В} = \frac{0,4}{0,8}$ = 0,5 ч = 1800 сек.
$t_{2А} = \frac{0,1}{40}$ = 0,0025 ч = 9 сек.
$t_{2Б} = \frac{0,2}{40}$ = 0,005 ч = 18 сек.
$t_{2В} = \frac{0,4}{40}$ = 0,01 ч = 36 сек.
$t_{3А} = \frac{0,1}{50}$ = 0,002 ч = 7,2 сек.
$t_{3Б} = \frac{0,2}{50}$ = 0,004 ч = 14,4 сек.
$t_{3В} = \frac{0,4}{50}$ = 0,008 ч = 28,8 сек.
$t_{4А} = \frac{0,1}{60}$ = 0,002 ч = 6 сек.
$t_{4Б} = \frac{0,2}{60}$ = 0,003 ч = 12 сек.
$t_{4В} = \frac{0,4}{60}$ = 0,007 ч = 24 сек.
$t_{5А} = \frac{0,1}{80}$ = 0,00125 ч = 4,5 сек.
$t_{5Б} = \frac{0,2}{80}$ = 0,0025 ч = 9 сек.
$t_{5В} = \frac{0,4}{80}$ = 0,005 ч = 18 сек.
$t_{6А} = \frac{0,1}{90}$ = 0,001 ч = 4 сек.
$t_{6Б} = \frac{0,2}{90}$ = 0,002 ч = 8 сек.
$t_{6В} = \frac{0,4}{90}$ = 0,004 ч = 16 сек.
$t_{7А} = \frac{0,1}{120}$ = 0,0008 ч = 3 сек.
$t_{7Б} = \frac{0,2}{120}$ = 0,002 ч = 6 сек.
$t_{7В} = \frac{0,4}{120}$ = 0,003 ч = 12 сек.
Ответ:
Черепаха преодолеет
100 м за 450 сек;
200 м за 900 сек;
400 м за 1800 сек;
Слон преодолеет
100 м за 9 сек;
200 м за 18 сек;
400 м за 36 сек;
Кенгуру преодолеет
100 м за 7,2 сек;
200 м за 14,4 сек;
400 м за 28,8 сек;
Заяц − русак преодолеет
100 м за 6 сек;
200 м за 12 сек;
400 м за 24 сек;
Страус преодолеет
100 м за 4,5 сек;
200 м за 9 сек;
400 м за 18 сек;
Антилопа гну преодолеет
100 м за 4 сек;
200 м за 8 сек;
400 м за 16 сек;
Гепард преодолеет
100 м за 3 сек;
200 м за 6 сек;
400 м за 12 сек.

Задание №94

Чему равна скорость звука в воздухе (при 0 °С), если он за 1,5 с распространяется на 495 м?

Решение

Дано:
t = 1,5 с;
S = 495 м.
Найти:
v − ?
Решение:
$v = \frac{S}{t}$;
$v = \frac{495}{1,5} = 330$ м/с.
Ответ: 330 м/с.

Задание №95

Лифт поднимается равномерно со скоростью 3 м/с. На какую высоту он поднимется за 10 с?

Решение

Дано:
v = 3 м/с;
t = 10 c.
Найти:
S − ?
Решение:
S = vt;
S = 3 * 10 = 30 м.
Ответ: 30 м.

Задание №96

За какое время плывущий по течению плот пройдёт путь 1,5 км, если скорость течения реки равна 0,5 м/с?

Решение

Дано:
v = 0,5 м/с;
S = 1,5 км.
Найти:
t − ?
СИ:
S = 1500 м.
Решение:
$t = \frac{S}{v}$;
$t = \frac{1500}{0,5} = 3000 $ с.
Ответ: 3000 с.

Задание №97

Скорость роста гриба в тёплую погоду равна 4 мм/мин.
На сколько вырос бы гриб, если бы он рос с такой скоростью 5 ч?

Решение

Дано:
v = 4 мм/мин.;
t = 5 ч.
Найти:
h − ?
СИ:
t = 300 мин.
Решение:
h = v * t;
h = 4 * 300 = 1200 мм = 1,2 м.
Ответ: 1,2 м.

Задание №98

За какое время человек преодолеет олимпийские дистанции 100, 200 и 400 м на велосипеде (40 км/ч), мотоцикле (120 км/ч), гоночном автомобиле (260 км/ч)?

Решение

Дано:
$v_{вел}$ = 40 км/ч;
$v_{мот}$ = 120 км/ч;
$v_{авт}$ = 260 км/ч;
$S_{1}$ = 100 м;
$S_{2}$ = 200 м;
$S_{3}$ = 400 м;
Найти:
t − ?
СИ:
$S_{1}$ = 0,1 км;
$S_{2}$ = 0,2 км;
$S_{3}$ = 0,4 км
Решение:
$t = \frac{S}{v}$;
$t_{1вел} = \frac{0,1}{40} = 0,0025$ ч = 9 с;
$t_{2вел} = \frac{0,2}{40} = 0,005$ ч = 18 с;
$t_{3вел} = \frac{0,4}{40} = 0,01$ ч = 36 с;
$t_{1мот} = \frac{0,1}{120} = 0,0008$ ч = 3 с;
$t_{2мот} = \frac{0,2}{120} = 0,002$ ч = 6 с;
$t_{3мот} = \frac{0,4}{120} = 0,003$ ч = 12 с;
$t_{1авт} = \frac{0,1}{260} = 0,0004$ ч = 1,4 с;
$t_{2авт} = \frac{0,2}{260} = 0,0008$ ч = 2,8 с;
$t_{3авт} = \frac{0,4}{260} = 0,0015$ ч = 5,5 с.
Ответ:
Человек преодолеет на велосипеде олимпийские дистанции:
100 м за 9 с;
200 м за 18 с;
400 м за 36 с;
На мотоцикле:
100 м за 3 с;
200 м за 6 с;
400 м за 12 с;
На гоночном автомобиле:
100 м за 1,4 с;
200 м за 2,8 с;
400 м за 5,5 с.

Задание №99

Свет распространяется со скоростью 300 000 км/с. За какое время он проходит расстояние от Солнца до Земли, равное 150 млн км? Определите, какое примерно расстояние проходит Земля вокруг Солнца за год.

Решение

Дано:
v = 300 000 км/с;
$S_{1}$ = 150 млн км;
$t_{2}$ = 1 год.
Найти:
$t_{1}$ − ?
$S_{2}$ − ?
СИ:
1 год = 8760 ч;
Решение:
$t = \frac{S}{v}$;
$t_{1} = \frac{150000000}{300000} = 500$ с = 8 мин. 20 сек.;
S = vt;
$v = \frac{300 000}{\frac{1}{3660}} = 1,08 * 10^{9}$ км/ч;
$S_{2} = 1,08 * 10^{9} * 8760 = 9,46 * 10^{12} км = 9,46 * 10^{15}$ м.
Ответ: 8 мин. 20 сек.; $9,46 * 10^{15}$ м.

Задание №100

Бамбук растёт со скоростью 2 см/ч. Чему будет равна высота растения через неделю?

Решение

Дано:
v = 2 см/ч;
t = 1 неделя.
Найти:
h − ?
СИ:
t = 168 ч.
Решение:
h = v * t;
h = 2 * 168 = 336 см или 3,36 м.
Ответ: 3,36 м.

Задание №101

Сколько времени была в полёте летучая рыба, если она пролетела над водой 150 м со скоростью 25 км/ч?

Решение

Дано:
v = 25 км/ч;
S = 150 м;
Найти:
t − ?
СИ:
$v =\frac{25 * 1000}{3600} = 6,94$ м/с;
Решение:
$t = \frac{S}{v}$;
$t = \frac{150}{6,94} = 21,6$ с;
Ответ: 21,6 с.

Задание №102

Автомобиль движется равномерно со скоростью 40 м/с в течение 30 с. Какой путь пройдёт он за это время? Постройте график пути автомобиля.

Решение

Дано:
v = 40 м/с;
t = 30 c ;
Найти:
S − ?
Решение:
S = v * t;
S = 40 * 30 = 1200 м = 1,2 км.
Ответ: 1,2 км.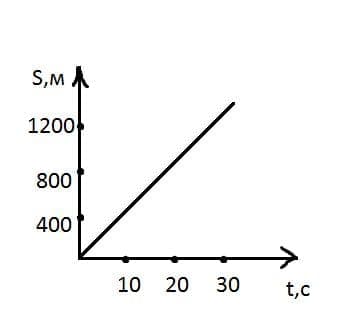

Задание №103

Считая первую космическую скорость (скорость, необходимую для того, чтобы тело могло покинуть Землю и стать искусственным спутником Земли) равной приблизительно 8 км/с, выразите её в км/ч. За какое время с такой скоростью можно было бы пролететь расстояние, равное длине земного экватора?

Решение

Дано:
v = 8 км/с;
S = 40 075 км;
Найти:
v (км/ч) − ?
t − ?
Решение:
$v = \frac{8}{\frac{1}{3600}} = 28800$ км/ч;
$t = \frac{S}{v}$;
$t = \frac{40075}{28800} = 1,39$ ч = 83 мин.
Ответ: 28800 км/ч; 83 мин.

Задание №104

Вторая космическая скорость (скорость, необходимая для того, чтобы тело могло покинуть Землю и, как планеты, двигаться вокруг Солнца) равна приблизительно 11,2 км/с. Выразите эту скорость в км/ч. За какое время, двигаясь с такой скоростью, можно было бы долететь до Луны, если расстояние от Земли до Луны равно 384 000 км?

Решение

Дано:
v = 11,2 км/с;
S = 384 000 км;
Найти:
v (км/ч) − ?
t − ?
Решение:
$v = \frac{11,2}{\frac{1}{3600}} = 40320$ км/ч;
$t = \frac{S}{v}$;
$t = \frac{384 000}{40320} = 9,52$ ч = 9 ч. 31 мин.
Ответ: 40320 км/ч; 9 ч. 31 мин.

Задание №105

Третья космическая скорость (скорость, необходимая для того, чтобы тело могло покинуть Солнечную систему) равна приблизительно 16,5 км/с. Выразите эту скорость в км/ч. За какое время, двигаясь с такой скоростью, можно было бы пролететь расстояние от Земли до Марса, равное 56 млн км?

Решение

Дано:
v = 16,5 км/с;
S = 56 млн км;
Найти:
v (км/ч) − ?
t − ?
Решение:
$v = \frac{16,5}{\frac{1}{3600}} = 59400$ км/ч;
$t = \frac{S}{v}$;
$t = \frac{56000000}{59400} = 943$ ч = 39 суток.
Ответ: 59400 км/ч; 39 суток.