Задание №1429
Рассмотрите таблицу.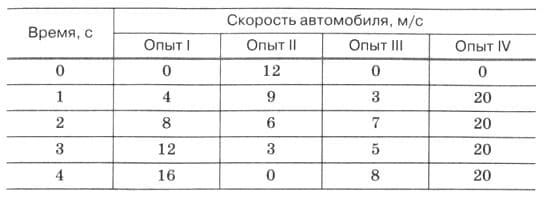
Ответьте на следующие вопросы:
а) Как двигался автомобиль в каждом из опытов?
б) Чему равно ускорение в каждом из опытов?
Решение
а) Опыт I − равноускоренное движение.
Опыт II − равнозамедленное движение.
Опыт III: 1−2 с. − равноускоренное движение; 2−3 с. − равнозамедленное движение; 3−4 с. − равноускоренное движение.
Опыт IV − равномерное движение.
б) $v = v_{0} + at$;
$v - v_{0} = at$;
$a= \frac{v– v_{0}}{t}$;
Опыт I:
$v_{0} = 0$; v = 16 м/с; t = 4 c;
$a= \frac{16 - 0}{4} = 4 м/с^{2}$;
Опыт II:
$v_{0} = 12$; v = 0 м/с; t = 4 c;
$a= \frac{0 - 12}{4} = -3 м/с^{2}$;
Опыт III:
1 − 2 с: $v_{0} = 0$; v = 7 м/с; t = 2 c;
$a= \frac{7 - 0}{2} = 3,5 м/с^{2}$;
2 − 3 с: $v_{0} = 7$м/с; v = 5 м/с; t = 1 c;
$a= \frac{5 - 7}{1} = -2 м/с^{2}$;
3 − 4 с: $v_{0} = 5$м/с; v = 8 м/с; t = 1 c;
$a= \frac{8 - 5}{1} = 3 м/с^{2}$;
Опыт IV: a = 0.
Задание №1430
С каким ускорением движется гоночный автомобиль, если его скорость за 6 с увеличивается от 144 до 216 км/ч?
Решение
Дано:
t = 6 c;
$v_{0} = 144$ км/ч;
$v = 216$ км/ч.
Найти:
a − ?
СИ:
$v_{0} = 40$ м/с;
$v = 60$ м/с.
Решение:
Уравнение скорости:
$v = v_{0} + at$;
$a = \frac{v – v _{0}}{t}$;
$a = \frac{60 - 40}{6} = 3,3 м/с^{2}$.
Ответ: 3,3 $м/с^{2}$.
Задание №1431
Рассчитайте модуль ускорения автомобиля, движущегося со скоростью 36 км/ч, если он останавливается в течение 10 с.
Решение
Дано:
t = 10 c;
$v_{0} = 36$ км/ч.
Найти:
a − ?
СИ:
$v_{0} = 10$ м/с.
Решение:
Уравнение скорости при торможении:
$v = v_{0} - at$;
Т.к. автомобиль остановился, то v = 0.
$v = at$;
$a = \frac{v}{t}$;
$a = \frac{10}{10} = 1 м/с^{2}$.
Ответ: 1 $м/с^{2}$.
Задание №1432
За какое время автобус, двигаясь с ускорением 0,4 $м/с^{2}$, увеличит свою скорость с 12 до 20 м/с?
Решение
Дано:
a = 0,4 $м/с^{2}$;
$v_{0} = 12$ м/с;
$v = 20$ м/с.
Найти:
t − ?
Решение:
Уравнение скорости:
$v = v_{0} + at$;
$t = \frac{v – v _{0}}{a}$;
$t = \frac{20 - 12}{0,4} = 20 $ с.
Ответ: 20 с.
Задание №1433
Автомобиль, движущийся с ускорением 1 $м/с^{2}$, остановился через 10 с. Определите его скорость в начале торможения.
Решение
Дано:
a = 1 $м/с^{2}$;
t = 10 c.
Найти:
$v_{0}$ − ?
Решение:
Уравнение скорости:
$v = v_{0} - at$;
Так как автомобиль остановился, то v = 0.
$v_{0} = at$;
$v_{0} = 1 * 10 = 10$ м/с.
Ответ: 10 м/с.
Задание №1434
С каким ускорением двигались санки, если они скатились без начальной скорости с горы длиной 36 м за 60 с?
Решение
Дано:
t = 60 c;
S = 36 м.
Найти:
a − ?
Решение:
Уравнение движения:
$S = v_{0}t + \frac{at^{2}}{2}$.
Санки начинают движение, поэтому $v_{0} = 0$.
$S = \frac{at^{2}}{2}$;
$2S = at^{2}$;
$a = \frac{2S}{t^{2}}$;
$a = \frac{2 * 36}{60^{2}} = 0,02 м/с^{2}$.
Ответ: 0,02 $м/с^{2}$.
Задание №1435
Какую скорость развивает мотоциклист за 15 с, двигаясь из состояния покоя с ускорением 1,3 $м/с^{2}$?
Решение
Дано:
t = 15 c;
a = 1,3 $м/с^{2}$.
Найти:
v − ?
Решение:
Уравнение скорости:
$v = v_{0} + at$;
Мотоциклист начинает движение, поэтому $v_{0} = 0$.
$v = at$;
$v = 1,3 * 15 = 19,5$ м/с.
Ответ: 19,5 м/с.
Задание №1436
За какое время ракета приобретает первую космическую скорость 7,9 км/с, двигаясь с ускорением 50 $м/с^{2}$?
Решение
Дано:
a = 50 $м/с^{2}$;
v = 7,9 км/с.
Найти:
t − ?
СИ:
v = 7900 км/с.
Решение:
Уравнение скорости:
$v = v_{0} + at$;
Ракета начинает движение, поэтому $v_{0} = 0$.
$v = at$;
$t = \frac{v}{a}$;
$t = \frac{7900}{50} = 158 $ с.
Ответ: 158 с.
Задание №1437
Рассчитайте длину взлётной полосы, если скорость самолёта при взлете 300 км/ч, а время разгона 40 с.
Решение
Дано:
t = 40 c;
v = 300 км/ч.
Найти:
S − ?
СИ:
v= 83,3 м/с.
Решение:
Ракета начинает движение, поэтому $v_{0} = 0$.
$S = \frac {v_{0} + v}{2} * t$;
$S = \frac {83,3}{2} * 40 = 1666$ м ≈ 1,67 км.
Ответ: 1,67 км.
Задание №1438
Поезд через 10 с после начала движения приобретает скорость 0,6 м/с. Через какое время от начала движения скорость поезда станет равной 9 м/с? Какой путь пройдёт поезд за это время?
Решение
Дано:
t = 10 c;
v = 0,6 м/с;
$v_{1} = 9$ м/с;
Найти:
$t_{1}$ − ?
$S_{1}$ − ?
Решение:
Уравнение скорости:
$v = v_{0} + at$;
Поезд начинает движение, поэтому $v_{0} = 0$.
v = at;
$a = \frac{v}{t}$;
$a = \frac{0,6}{10} = 0,06 м/с^{2}$;
Уравнение скорости:
$v_{1} = at_{1}$;
$t_{1} = \frac{v_{1}}{a}$;
$t_{1} = \frac{9}{0,06} = 150$ с;
Уравнение движения:
$S_{1} = v_{0}t_{1} + \frac {at_{1}^{2}}{2}$;
Т.к. $v_{0} = 0$, то $S = \frac {at_{1}^{2}}{2}$;
$S = \frac {0,06 * 150^{2}}{2} = 675$ м.
Ответ: 150 с; 675 м.
Задание №1439
Чему равна длина пробега при посадке самолёта, если его посадочная скорость 140 км/ч, а ускорение при торможении 2 $м/с^{2}$?
Решение
Дано:
a = 2 $м/с^{2}$;
$v_{0} = 140$ км/ч.
Найти:
S − ?
СИ:
$v_{0} = 38,9$ м/с.
Решение:
Уравнение скорости при торможении:
$v = v_{0} - at$;
Самолет тормозит, поэтому v = 0.
$v_{0} = at$;
$t = \frac{v_{0}}{a}$;
Уравнение движения:
$S = \frac {v_{0} + v}{2} * t$;
Т.к. v = 0, то $S = \frac {v_{0}t}{2} = \frac {v_{0}* \frac{v_{0}}{a}}{2} = \frac {v_{0}^{2}}{2a}$;
$S = \frac {38,9^{2}}{2 * 2} = 378$ м.
Ответ: 378 м.
