Задание №13
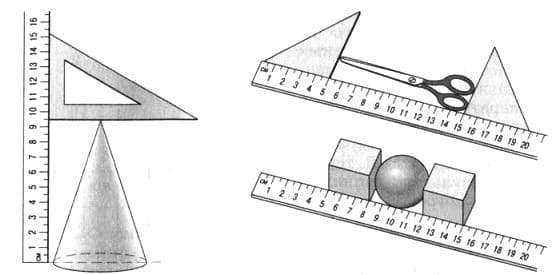
Определите цену деления и предел измерения линеек, изображенных на рисунке 1. Чему равны высота конуса, длина ножниц и диаметр шара? Результаты запишите с учётом погрешности измерения.
рис. 1
Ответ
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
Цена деления = $\frac{11-10}{2}$ = 0,5 см
Предел измерения − 0,5 см − 21 см
Высота конуса − 9,5 см
Длина ножниц − 10,0 см
Диаметр шара − 4 см.
Задание №14
В мензурке конической формы с сужением вниз расстояния между соседними делениями равны. Одинакова ли цена деления по всей шкале мензурки?
Ответ
Из−за конической формы цена деления мензурки неравномерная, цена деления увеличивается снизу вверх.
Задание №15
Определите цену деления и предел измерения каждой из мензурок, изображённых на рисунке 2, если их вместимость выражена в миллилитрах. Чему равен объём воды, налитой в каждую мензурку; объём тела, погруженного в мензурку? Результаты запишите с учётом погрешности измерения.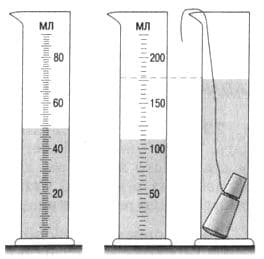
рис. 2
Решение
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
Цена деления мензурки слева − 1 мл. Погрешность измерения − 0,5 мл. Предел измерения − 90 мл.
Объём воды с учетом погрешности измерения − (49 ± 0,5) мл.
Цена деления мензурки справа − 5 мл. Погрешность измерения − 2,5 мл. Предел измерения − 225 мл.
Объём воды с учетом погрешности измерения − (110 ± 2,5) мл.
$V_{т} = V_{1}-V_{0} = 175 мл - 110 мл = 65$ мл.
Объём тела, погруженного в мензурку, с учетом погрешности измерения − (65 ± 2,5) мл.
Задание №16
Какому основному требованию должны соответствовать точные часы? Какие часы в большей мере соответствуют этому требованию?
Ответ
Основное требование − точность хода. Этому требованию соответствуют астрономические и атомные часы.
Задание №17
Измеряя длину комнаты, учащийся ошибся на 4 см, а измеряя длину шариковой ручки − на З мм. Какую долю (в %) измеряемой длины составляла ошибка в первом и втором случаях, если длина комнаты 4,8 м, а шариковой ручки − 12 см? В каком случае измерение выполнено точнее?
Решение
4,8 м = 480 см.
$\frac{4}{480}$ * 100 % = 0,83 % − доля ошибки в первом случае.
12 см = 120 мм.
$\frac{3}{120}$ * 100 % = 2,5 % − доля ошибки во втором случае.
Вывод. В первом случае измерение выполнено точнее.

