Задание №1943
Вторичная обмотка трансформатора имеет 60 витков. Сколько витков в первичной обмотке, если трансформатор понижает напряжение от 220 до 50 В?
Решение
Дано:
$U_{1} = 220$ В;
$U_{2} = 50$ В;
$N_{2} = 60$ витков.
Найти:
$N_{1}$ − ?
Решение:
$\frac{U_{1}}{U_{2}}= \frac{N_{1}}{N_{2}}$;
$N_{1} = \frac{U_{1}N_{2}}{U_{2}}$;
$N_{1} = \frac{220 * 60}{50} = 264$ витка.
Ответ: 264 витка.
Задание №1944
Электрический звонок рассчитан на напряжение 6 В. С помощью небольшого трансформатора он может быть включён в осветительную сеть напряжением 220 В. Начертите схему такого включения. Укажите отношение числа витков первичной и вторичной обмоток трансформатора.
Решение
Схема включения электрического звонка в сеть.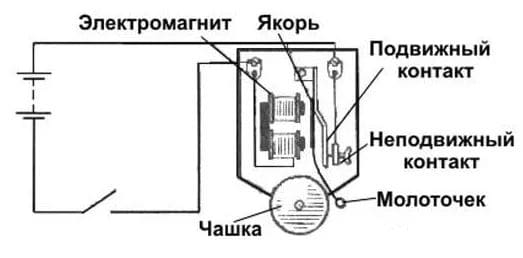 Рассчитаем отношение числа витков первичной и вторичной обмоток трансформатора.
Рассчитаем отношение числа витков первичной и вторичной обмоток трансформатора.
$U_{2} = 6$ В;
$U_{1} = 220$ В
$\frac{N_{1}}{N_{2}} = \frac{U_{1}}{U_{2}}$;
$\frac{N_{1}}{N_{2}} = \frac{220}{6} = 37$.
Ответ: 37.
Задание №1945
Что является источником электромагнитных колебаний:
а) в цепи катушки и гальванометра (см. рис. 310);
б) в осциллографе, подключённом в сеть (рис. 324, а);
в) в колебательном контуре (рис. 324, б)?
Какие возникают колебания в каждом случае − свободные или вынужденные?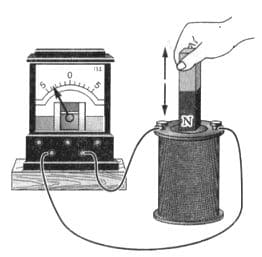 рис. 310
рис. 310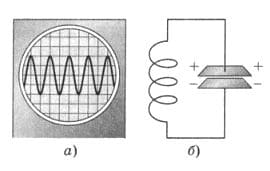 рис. 324
рис. 324
Решение
Источник электромагнитных колебаний:
а) Колеблющийся магнит;
б) Напряжение в сети;
в) Заряд конденсатора.
Свободные колебания в случае в), вынужденные − в случаях а) и б).
Задание №1946
Как изменится электроёмкость плоского конденсатора при увеличении расстояния между пластинами конденсатора в 4 раза?
Решение
Электроёмкость плоского конденсатора обратно пропорциональна расстоянию между пластинами и прямо пропорциональна их площади ($C = \frac{εε_{0}S}{d}$)
Таким образом, электроёмкость уменьшится в 4 раза.
Задание №1947
Как изменится электроёмкость плоского конденсатора при уменьшении площади пластин конденсатора в 2 раза?
Решение
Электроёмкость плоского конденсатора обратно пропорциональна расстоянию между пластинами и прямо пропорциональна их площади ($C = \frac{εε_{0}S}{d}$)
Таким образом, электроёмкость уменьшится в 2 раза.
Задание №1948
Конденсатору ёмкостью 10 мкФ сообщили заряд 4 мкКл. Какова энергия заряженного конденсатора?
Решение
Дано:
С = 10 мкФ;
q = 4 мкКл;
Найти:
W − ?
СИ:
$С = 10^{-5}$ Ф;
$q = 4*10^{-6}$ Кл;
Решение:
Ёмкость конденсатора равна:
$C = \frac{q}{U}$;
q = CU;
Найдем энергию конденсатора:
$W = \frac{CU^{2}}{2} = \frac{q^{2}}{2C}$;
$W = \frac{(4*10^{-6})^{2}}{2 * 10^{-5}} = \frac{16 * 10^{-12}}{2 * 10^{-5}} = 8 * 10^{-7}$ Дж = 800 нДж;
Ответ: 800 нДж.
Задание №1949
Имеется батарея, состоящая из двух конденсаторов ёмкостью по 10 мкФ каждый, соединённых параллельно. Чему равна ёмкость такой батареи?
Решение
Дано:
$С_{1} = С_{2} = 10$ мкФ.
Найти:
C − ?
СИ:
$С_{1} = С_{2} =10^{-5}$ Ф;
Решение:
При параллельном соединении конденсаторов емкость батареи равна сумме емкостей конденсаторов входящих в батарею:
$C= C_{1} + C_{2} = 2C_{1} $;
$С = 2 * 10^{-5}$ Ф = 20 мкФ.
Ответ: 20 мкФ.
Задание №1950
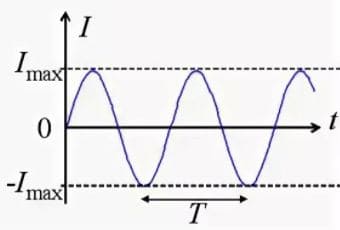
Конденсатор подключён к батарее с помощью переключателя в точке 1 (рис. 325). Что произойдёт, если переключатель соединить с конденсатором в точке 2? Будет ли изменяться сила тока в проводах, соединяющих конденсатор и катушку? Начертите график изменения силы тока.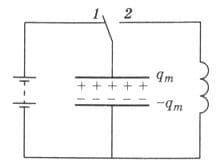 рис. 325
рис. 325
Решение
Если переключатель соединить с конденсатором в точке 2, то конденсатор начнет разряжаться и в цепи появится электрический ток.
Сила тока в проводах, соединяющих конденсатор и катушку, изменяется. Сила тока увеличивается постепенно в связи с явлением самоиндукции. ЭДС самоиндукции всегда возникает при появлении тока в цепи и препятствует его увеличению. В момент, когда конденсатор полностью разрядится, сила тока достигнет максимального значения. Как только сила тока и созданное током магнитное поле начнут уменьшаться, возникнет вихревое электрическое поле, которое направлено по току и поддерживает его, в результате конденсатор начнет перезаряжаться. Конденсатор перезаряжается до тех пор, пока сила тока, постепенно уменьшаясь, не станет равной нулю.